欧拉(Leonhard Euler,1707-1783)——生平与成就

要花多久才能写完一生的著作?这个问题的答案很简单:当然是一生的时间!那么,要花多久才能发表完一生的著作?对于欧拉来说,这个问题的答案是一个世纪(或者更长)。自1911年起,瑞士科学院开始发表欧拉著作全集。目前,已经发表了超过72卷的著作,未发表的还更多。这不应该让我们感到意外。一位知名的科学史家的估计是,欧拉一个人就撰写了整个18世纪涵盖数学、物理、力学、天文学以及航海学方面著作总量的25%。他是有史以来最多产的数学家。
和不少本书讲述到的数学家一样,很难在他的家族中找到欧拉的天才传承的踪迹。他的母亲玛格丽塔·布鲁克出身于受过良好教育的牧师世家,而他的父亲保卢斯·欧拉也是一位牧师,是欧拉家族中第一位受过良好教育的人。保卢斯的祖父汉斯-乔治·欧拉是位梳子匠,于1594年定居到巴塞尔。保卢斯的特别之处在于他确实聆听过伟大的雅各布·伯努利(1654-1705)在巴塞尔举办的数学演讲,而伯努利是出过八位伟大数学家的天才世家中的第一位伟大数学家。
玛格丽塔和保卢斯与1701年成婚,六年后的4月15日,莱昂哈德·欧拉出生在瑞士的巴塞尔。那时,巴塞尔还是瑞士的十三个共和国之一,人口约17,000,大部分是从欧洲天主教环境中移民出来的加尔文教徒。其中就有雅各布·伯努利的先祖,他们在16世纪后期从比利时逃了出来。
儿子出世不久,保卢斯在巴塞尔郊外5英里的里恩镇获得了教职,此时家庭里又添了三个小孩。保卢斯自己担当他儿子的老师,也许还教授了一些从伯努利的演讲中获得的数学眼光。八岁的时候,欧拉来到巴塞尔与他寡居的祖母玛丽亚·玛格达琳娜·布鲁克-法伯一起生活,以便他就学于巴塞尔中学。尽管中学提供了优秀的拉丁语和希腊语教育,它却没有任何数学方面的课程。当地人觉得对于年轻学子而言数学太难了一点。为了填补这一课程上的空白,保卢斯聘请了年轻的神学家布尔克哈特作为他儿子的数学专门导师。
5年后,欧拉13岁的时候进入了巴塞尔大学。本科的时候他学习的是神学。这段时间大学的记录表明他显露了对于经典的异乎寻常的精通,他能背诵维吉尔长达12,000行的诗篇埃涅阿斯纪。没有记录表明这段时间他有什么数学上的成果,不过应该是有一些的。
1723年欧拉获得了硕士学位,他忠诚地遵照这他父亲的意愿,继续留在学校以期获得神学博士学位。很快事情就发生了变化。他和约翰·伯努利二世(1710-1790)成为了朋友,他们一起参加约翰·伯努利一世(也就是一世的父亲,雅各布——也就保卢斯聆听的演讲的发言人——的兄弟)举办的演讲。在两位伯努利的影响下,年轻的欧拉开始浸淫于数学。约翰·伯努利一世很快就意识到欧拉绝顶的天才,为他提供私人讲习。不久约翰·伯努利一世会这样描述欧拉:
这位年轻人,有着令人羡慕的天才,其聪颖和精细让我们得以确信他是最伟大的,因为我们见证了他无需费力却驾轻就熟地就掌握了我们能预知的更高层次的数学中最隐秘的领域。
欧拉有很多机会来展示伯努利所提到的才华。1726年,巴黎学院举办了一次有奖征答,征求设立船上桅杆的最佳方式。尽管身处内陆的瑞士,对帆船毫无经验,欧拉提出的数学方案还是非常好并最终获得第二名。
同一年,欧拉在伯努利的指导下完成了《声音理论的论文》。这使得他有资格申请学校中空缺的物理教授职位。虽然伯努利鉴定地支持欧拉,学校还是采用其传统方法,也就是用抽签的方式将候选人名单减少到只有三位。欧拉不在其中。这一瑞士的损失将成为俄罗斯的收获。
1724年,也就是沙皇彼得大帝去世前一年,他发布了一项法令,要求在俄罗斯的新首都圣彼得堡建立一所科学院。彼得邀请了当时全欧洲最出色的学者前往学院,其中就有尼可拉斯·伯努利二世(1695-1726)和丹尼尔·伯努利(1700-1782)。他们一到圣彼得堡,就向学院推荐邀请欧拉——他们父亲最优秀的学生。尽管欧拉再也不会回到瑞士,但他终其一生一直保留着瑞士国籍。
彼得堡学院为欧拉提供了生理学主任的位置。欧拉很快就接受了并报名进入巴塞尔的医学院为这一新职位做准备——而这离他前往俄罗斯只有三天!实际上,欧拉选择无视他最初职位的细节,而进行着数学、物理和逻辑方面的讲课。
欧拉在生理学这个错配的位置上不会呆太久。丹尼尔·伯努利辞去了其物理主任的位置转而担任数学主任——该职位的第一任主任赫尔曼在1730年决定返回巴塞尔。于是欧拉就可以接任空缺的物理学教授一职。两年后,伯努利也返回了巴塞尔,于是欧拉就接任了数学主任之职。
彼得大帝在建立圣彼得堡学院的时候,也考虑了实际运用的一面。他希望籍此来讲俄罗斯带入现代化。在实用端,欧拉在勘察、制图、航海、以及海洋设施建造方面都做出了贡献。
欧拉在这些领域以及本身教授职位方面的收入使得他能考虑婚姻大事。他很快将注意力放在凯瑟琳·吉赛尔身上。她是一位瑞士艺术家的女儿,这位艺术家也在学院任教。莱昂哈德与凯瑟琳于1733年圣诞节后不久成婚。不到一年后,他们的长子约翰·阿尔布雷希特出世。在接下来的17年间,欧拉家族还会添丁12口,但只有5个孩子存活了下来并长大成人。
欧拉经常说他做出好多其最伟大的数学发现的时候,是一手抱着孩子,而别的孩子在他膝下游玩的时候。也许正是在这样的场景中,他做出了第一个这样的发现(本书有摘录)。其时当在18世纪30年代中,他初为人父之后不久。
对无穷数列的分析可以追溯到古希腊人对芝诺悖论的研究,最出名的当数亚里斯多德《物理》一书的第五卷。17世纪的新数学提供了新的工具,标志着进入了无穷数列分析的新纪元。
17世纪末,雅各布·伯努利证明调和级数:
\(\sum_{k=1}^{\infty} \frac {1}{k} = 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...\)
是发散的。然后他提出一个问题,即平方倒数之和:
\(\sum_{k=1}^{\infty} \frac {1}{k^2} = \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...\)
是否收敛呢?为了解决这个问题,伯努利将其注意力投向另一个无穷序列。
三角形数是那些从1到n的正整数相加得到的数。例如:1=1,3=1+2,6=1+2+3。其通式为:
\((n^2+n)/2=1+2+3+4+...+(n-1)+n\)
伯努利证明,三角形数的倒数的和:
\(\sum_{n=1}^{\infty}\frac{1}{\frac{n^2+n}{2}}\)
收敛于2。注意到\(\frac{1}{n^2}\leqslant \frac{2}{n^2+n}\),他很快就证明平方倒数之和收敛,其收敛值不会大于2。但是,他无法确定这个值是多少。伯努利写道:“若某君能成功找到彼之数值——迄今余等驽钝之人虽竭力求取却尚未成功——并予以通报,余等将不胜感激。”为了纪念伯努利,这个问题被称为巴塞尔问题。
没有记录表明,欧拉在巴塞尔就学于约翰·伯努利——也就是雅各布的弟弟——的时候学过数论。他对这个问题的兴趣似乎是在1729年由哥德巴赫引起的。这位哥德巴赫时任圣彼得堡学院首席常务秘书,也就是他提出了著名的哥德巴赫猜想:任何大于2的偶数都可以表示为两个素数之和。
欧拉于1731年开始研究巴塞尔问题,并于1735年将其解决。
尽管出人意表,可我找到了表示数列\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}\)……等等等等之和的一个优雅的表达式,其依赖于圆的面积……我发现,这个数列之和的六倍等于直径为1的圆的周长的平方。
这个数列之和等于\(\pi ^2 / 6\)!他的证明大致如下。
1715年,英国数学家泰勒证明,三角正弦函数可以用无穷级数来表示:
\(sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...\)
欧拉将这个等式的两边同除以\(x\),得到:
\(\frac{sin(x)}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+...\)
(需要注意的是,\(-\frac{1}{3!}\)是\(x^2\)这一项的系数。)正弦函数在所有\(x\)取值为\(\pm\pi\)时等于0,也就是说上述给出的等式有非零根形如\(\pm n\pi (n=1, 2, 3, ...)\)。
然后欧拉进行了一个重要的突破。对于n次多项式\(P(x)\),如果有非零根\(a_1, a_2, a_3, ... a_n\),且\(P(0)=1\),可以写成如下的形式:
\(P(x)=(1-\frac{x}{a_1}) \times (1-\frac{x}{a_2}) \times (1-\frac{x}{a_3}) \times...\times(1-\frac{x}{a_n})\)
他将有限项数多项式的这一特性扩展到我们刚给出的左边由正弦函数表示的那个无穷项数的多项式!这么一来他就得到:
\(\frac{sin(x)}{x}= (1-\frac{x}{\pi})(1+\frac{x}{\pi})(1-\frac{x}{2\pi})(1+\frac{x}{2\pi})(1-\frac{x}{3\pi})(1+\frac{x}{3\pi})... = (1-\frac{x^2}{\pi^2})(1-\frac{x^2}{4\pi^2})(1-\frac{x^2}{9\pi^2})\)
将等式右边展开,并且只看\(x^2\)项就得到:
\(-(\frac{1}{\pi^2}+\frac{1}{4\pi^2}+\frac{1}{9\pi^2}+...)=-\frac{1}{\pi^2}\sum_{n=1}^{\infty}\frac{1}{n^2}\)
就是\(\frac{sin(x)}{x}\)的展开中\(x^2\)的系数。我们应该记得,\(-\frac{1}{3!}\)即是\(x^2\)项的系数,于是等式左边就可以被\(-\frac{1}{6}\)替换,从而得到:
\(-\frac{1}{6}=-\frac{1}{\pi^2}\sum_{n=1}^{\infty}\frac{1}{n^2}\)
也就是说:
\(\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}\)
证毕!(Quod erat demonstrandum!)
用类似的方法,欧拉证明四次方倒数之和等于\(\pi^4/90\),六次方倒数之和等于\(\pi^6/945\),他一直算到26次方倒数之和等于\(76977927\times(2^{24}/27!)\times\pi^{26}\)。有趣的是,类似序列的奇数次方倒数之和至今还没有求出。
完成上述工作后不久,欧拉在1735年生病了,他的说法是“高烧不退”。经过长期的休养后终于恢复健康。但不论是发烧还是休养都没能延缓欧拉数学成果产出的速度。
1736年,欧拉发表了他所称之为“位置几何”(geometria situs)——研究的是位置间的关系,而不是数量间的关系——的系列成果中的第一篇。如今这一数学分支被称为拓扑学。
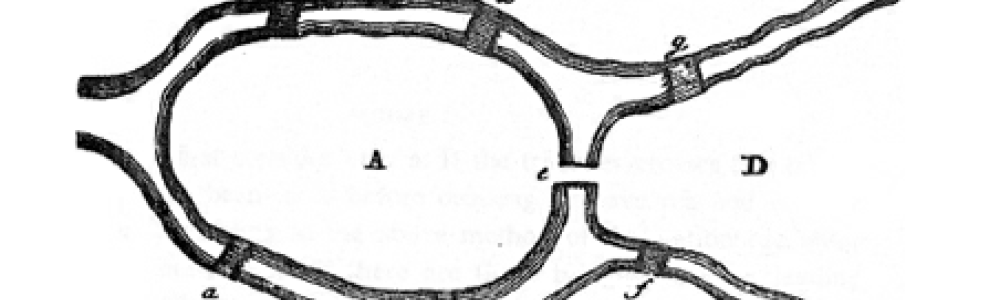
普雷格尔河的两道支流在(位于圣彼得堡西南600英里的)普鲁士城市柯尼斯堡的柯内霍普夫岛交汇。河上有七座桥。
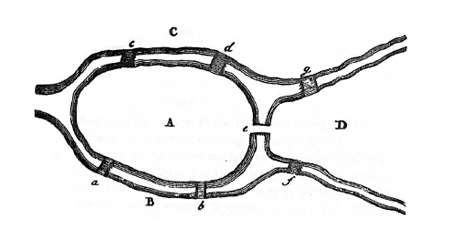
柯尼斯堡的居民一直在思考这样的一个问题:一个人能不能不行走过所有桥一次且仅一次?这个问题成为著名的柯尼斯堡的七桥问题。大多数人认为这样的一个行程是不可能的,但是没有人能证明。欧拉做到了!本书中选择的欧拉的第二部著作就是他对这个问题的分析。
欧拉意识到,解决这个问题的方法之一是简单地穷举所有可能的路线,且这些路线不会经过同一座桥多过一次。但是,这个方法不是他的兴趣所在。相反,他将问题进行一般化并考虑
任意河流及分叉的组合,以及任意数量的桥梁,确定是否有可能每座桥用到且只用到一次。
欧拉的观点是他应该先考虑穿越过的陆地的序列,而暂不考虑用了哪些桥梁。假定A,B,C和D是七桥问题中的陆地,那么ABDC代表了这样的一个穿越序列:从A到B到D再到C。欧拉先从最简单的情形开始分析问题:只考虑两个陆地A和B,由任意数量的桥梁连接。
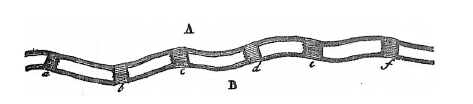
如果只有一座桥连到陆地A,那么A在穿越序列中只能出现一次才能保证该桥梁只被经过一次。如果有两座桥连到A,那么A可以在穿越序列中出现两次才能保证这两座桥只被经过一次。一般而言,如果有奇数N座桥连到A,那么A只能在穿越序列中出现\(\frac{N+1}{2}\)次,才能保证每座桥只被经过一次。
回到柯尼斯堡的特定问题,欧拉注意到每块陆地所连接的桥梁数目都是奇数:A有五座,B、C和D有三座。基于我们刚才讨论的结果,穿越序列必须包含三次A,和两次的B、C、D,总共在穿越序列中要出现9个字母。但是如果这七座桥只能被经过一次,那么这样的穿越序列将只包括A、B、C和D总共八次的穿越。虽然欧拉解决了七桥问题,但是他并没有就此止步。
他接着注意到,如果有偶数座桥连到A,那么A可以在穿越序列中出现\(\frac{N}{2}+1\)次——如果A是旅程的起点,或者\(\frac{N}{2}\)次——如果A不是旅程的起点,才能保证所有的桥梁只被经过一次。得到这个结论后,欧拉意识到:
当然,每条路线必得从某个区域出发,因此从连到各个区域的桥梁数目出发,我这样来确定出现在整条路径表达式中对应的字母的次数:如果桥梁的数目为奇数,我将其加1再除以2;如果是偶数,就直接除以2。如果这些结果之和等于桥梁的数量加上1,那么这样的旅程是可行的,但是它必须从那块有奇数座桥梁连接的区域开始。但如果这样的和比桥梁数目加1小1,旅程也是可行的,但要从那块有偶数座桥梁连接的区域开始,因为这样一来,其和实际上又被加上了1。
现代拓扑学中将地块和桥梁描述为顶点和连接顶点的边。
欧拉解决了七桥问题后不久,高热又一次侵袭了他。到1738年,他丧失了右眼的视力。
在此期间,彼得大帝的遗孀凯瑟琳一世女王延续着她丈夫未竟的俄罗斯自由化进程。但是她死于1727年,也就是欧拉来到俄罗斯的那年,而其后继者更迭频繁,且都是来自老派的俄罗斯贵族。随着时间的推移,那些想要将国家重归到老俄罗斯道路的贵族对外国人的疑心越来越重。俄罗斯东正教的圣议会反对学院,因为后者教授新科学,特别地,教授哥白尼的天文学。
俄罗斯在反自由化的道路上行进,在西方一位新的国王即位,并计划对他的国家进行自由化。腓特烈二世,也就是腓特烈大帝于1740年继承了普鲁士王伟,并立即展开计划重新在首都柏林建立能与巴黎、伦敦、圣彼得堡等学院媲美的学院。欧拉收到了加入这个新学院的第一批邀请。
欧拉很快接受了邀请。圣彼得堡学院的新院长舒马赫只是一名官僚,他的主要目标——按照欧拉的说法——就是“镇压所有的才华,只要它有对当局不利的苗头”。用他的话来说,俄罗斯已经成为“凡说话者皆岌岌可危的国家”。欧拉夫人也迫切想离开圣彼得堡,怕频繁发生的火灾会烧毁他们的木屋。
欧拉于1741年6月离开圣彼得堡,在俄罗斯新首都呆了14年,发表了超过50本的著作和文章。一个月后他抵达柏林,并将在那儿呆上25年。
在柏林期间,他继续着多产的生涯。他是如此多产以致于他的新论文(总共大约有380篇)填满了柏林学院(以法文发表)和圣彼得堡学院(以拉丁文发表)的所有期刊。在此期间,欧拉也写了不少很受欢迎的教科书。他的《数学》是第一本以新的无穷小量微积分框架来展示牛顿运动定律的著作。
欧拉的《无穷分析导论》最早于1748年发表,也是他这段时期最出名的教科书。在这部两卷本的著作中,欧拉展示了平方倒数之和,以及几乎当时所有已知的其它数学分析结果,且没有用到较新也较具争议的无穷小量微积分技术。这本教科书为数个时代的读者引入了cos和sin等三角函数符号,用来代表圆的周长与直径之比的π符号,i作为根号-1的符号,以及与这些符号齐名的自然对数之底的符号e。就以其影响而言,不少数学史家将欧拉的《导论》与欧几里德的《原本》相提并论,是丝毫不令人奇怪的。
这段时间欧拉所作的销量最好的书籍是他为年轻的安哈特-迪索公主进行初等科学介绍时所编写的。欧拉将这些课程汇编为《欧拉为一位德国公主写的关于自然哲学中不同主题的信件》发表。它包含200多封信件,主题涵盖逻辑、语言、天文、引力、光、声以及磁等诸多领域。另外,还有一些信件是针对特定的主题而写,比如天空为何是蓝色的,月亮为何在初生时看上去更大,热带地区的山顶为何寒冷等等等等。另外,由于欧拉还负责为公主提供道德方面的培养,《信件》中还包括他关于罪恶的源头,罪犯的改造等方面的思想。
除了写作,欧拉还挤出时间进行很多其他更实际的工作。国王安排欧拉从事多项对王国有利的工作。其中包括修正费诺运河的基准,这条运河是东普鲁士重要的商业通道,组织国家彩票,并就关于保险、年金、寡妇恤金等方面的问题为政府提供建议。欧拉还监管学院的天文台和植物园。腓特烈甚至要求欧拉监管皇家夏日行宫无忧宫的供水系统的建造。
学院第一任院长皮埃尔·德·莫佩尔蒂于1759年去世后,欧拉希望能被命名为继任者。毕竟他是中世纪欧洲最伟大的科学家。但是国王要求的资历中,欧拉缺少几个关键的元素。他是瑞士人而不是法国人。另外,当时欧拉一家住在柏林郊外的一个农场中,显然这和腓特烈所极为欣赏的世俗风尚大相径庭。最终腓特烈任命了另一位法国人达兰贝尔作为学院的新院长。欧拉十分失望,立马决定离开柏林。
在柏林呆的这25年间,欧拉和他在圣彼得堡的前同事保持着非常真诚的交流。为了感谢他之前所作的工作,圣彼得堡的学院给他发放定期的补贴,即便俄罗斯和普鲁士还在进行着七年战争期间。
18世纪60年代中期,继位的凯瑟琳女王权位已然稳固,于是欧拉欣然接受邀请回到圣彼得堡。当然,欧拉需要腓特烈大帝的同意方能离开柏林。他先是给国王写信请求恩准,但是国王根本拒绝回复。又写了两封请辞信后,国王回复说,欧拉你应该撤回请辞少来烦我。直到凯瑟琳女王亲自介入后,才说服腓特烈放走欧拉。国王写了一张简明扼要的便签,说道:“你4月30日的来信收悉。朕已恩准你辞职前往俄罗斯。”
欧拉一家于1766年夏回到圣彼得堡,住在涅瓦河畔的一所房子里,离学院也很近。回到圣彼得堡后,欧拉的生活也不轻松。在柏林的最后几年,欧拉还算好的那只左眼患上了白内障。回到俄罗斯后,就越来越严重了,最终决定用手术摘除晶状体。一开始看起来手术很成功,但随之而来的并发症使得欧拉丧失了使用左眼的能力,其余生只有非常微弱的视力。
不久之后,凯瑟琳最担心的事情还是发生了。1771年5月,一场大火席卷了圣彼得堡,烧毁了涅瓦很畔超过500所的房子,欧拉家的房子也不能幸免。多亏了一位来自巴塞尔的勇敢的手工艺人彼得·格林,才将几乎全盲的欧拉和他的手稿从熊熊燃烧着的屋子里给救了出来。
两年半后,欧拉不幸丧偶而成了鳏夫,她夫人于1773年11月突然去世,享年66岁。失去了视力,失去了妻子,欧拉还是继续着他的工作。1775年期间,他平均每周写一篇数学论文,他口述,书记员誊写。毫无疑问,欧拉惊人的记忆力——十几岁时就能背诵《埃涅阿斯纪》——使他还能继续其研究工作。本书中选择的欧拉的第二篇著作,即证明所有整数都可以表达为不超过四个整数平方和的证明,就来自这一阶段。
1621年,法国数学家巴协猜想说,所有正整数可以表述为不超过四个平方数的和。著名的业余数学家费马在这个问题上做了一些研究但是无法提供一个令人满意的证明。欧拉做到了。
欧拉在其证明中用的是求模运算,并依赖于这样一个关键事实,即如果k无法被N整除,那么\((aN+k)^2\)和\((aN-k)^2\)除以N的时候是同模(余数相等)的。因此如果N是的奇素数,那么形如aN+b(b=1, 2, ... N-1)的数中,一半是以N为模的平方数,而另一半不是。
欧拉发表该证明的几乎同时,英国数学家华林扩展了巴协原来的猜想,并不加证明地断言,每个正整数还可以表述为不超过9个立方数值和,不超过19个四次方数之和,更一般的,对于任何次方数K,存在值S,使得所有正整数可以表示为不超过S个K次方数之和。1909年,德国数学家希尔伯特证明了华林的猜想!
在妻子去世后,欧拉继续活了10年,并在1776年7月和先妻之同母异父的妹妹结婚。1783年9月初他开始患上头晕症。那一月7号那天,对于欧拉来说是平常的一天。在早上他给一位孙辈授课,然后开始计算新近发现的海王星的轨道。当日稍晚,他正在饮着茶,抽着烟斗。烟斗从他手中滑落。他试图捡起烟斗,却摔倒在地,呼叫着“我要死了!”他很快就不行了,中风了。他再也没能恢复清明,并于当晚去世。学会的期刊用了20年的时间才发表完所有他留下来的手稿。