题目
分析
这是一道典型的动态规划(DP)题,用来入门非常不错。
我们看一个典型的布局:
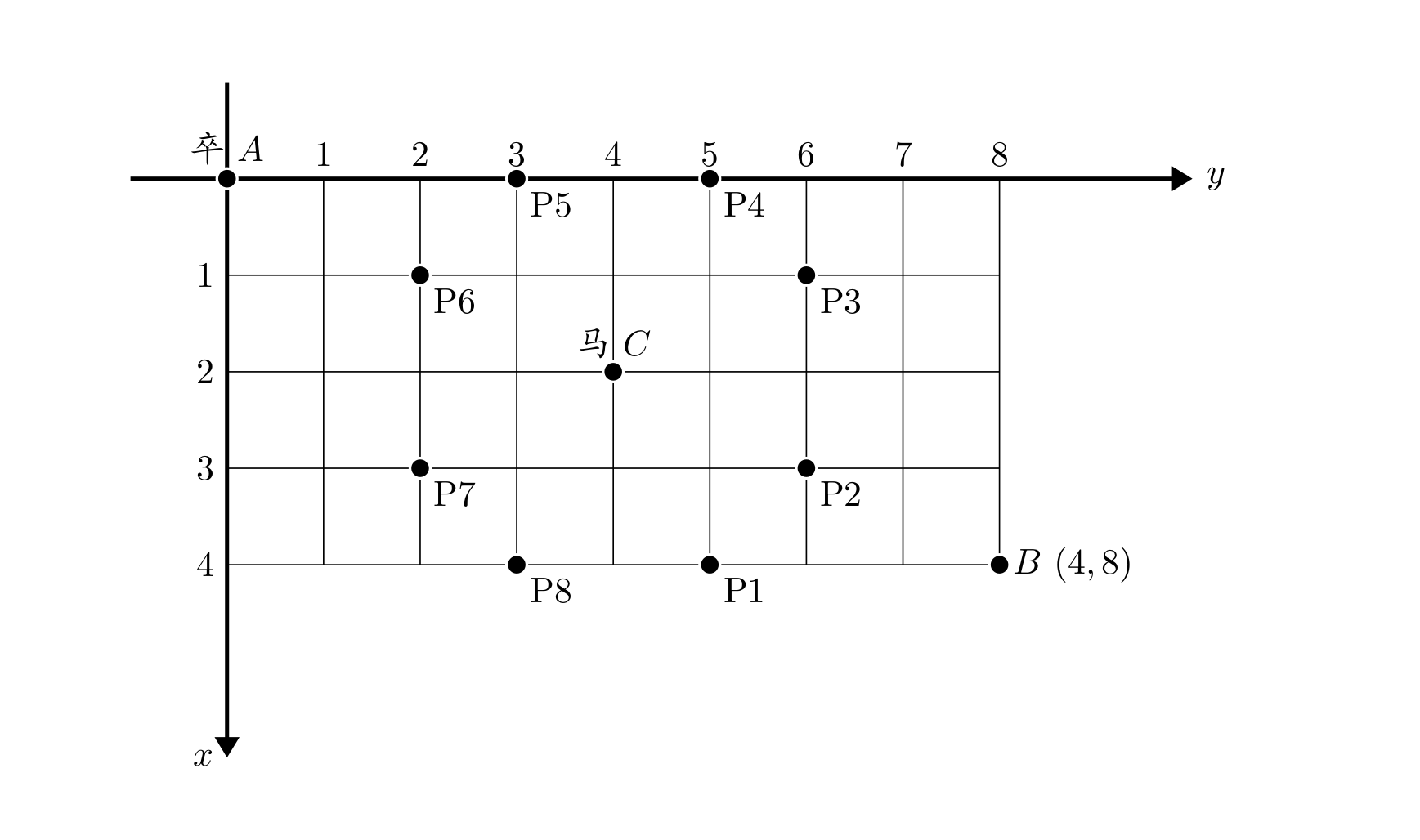
如果我们不考虑马的存在,那么根据卒行进的规则,很容易就能得到状态转移方程:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];也就是说,对于一个常规的格子,可以从上方或者左方走到这里。
考虑了马的存在后,马所在的位置以及所有马能控制的位置是无法通过的,也就是说走到这里就“死路”了,无法继续向右或者向下,那这些格子的路径数量必须设置为0。(如图示的P1-P8点和点C。)
另外,DP问题都需要进行一些“状态”的初始化。在这个例子中,我们要考虑多一些:
- 第一行一般而言,都可以初始化为
1——因为确实只有一种走法。但这里要考虑马的控制点在第一行的情况。如果第一行某一列的点被马控制,那该点设置为0而不是1,而且所有后续的点也都是0。 - 第一列的情况类似。
另外,计算马的控制点有一些技巧,可以用到曼哈顿距离和切比雪夫距离。这里不展开,而直接给出马的控制点的判定公式:
(abs(kx - x) + abs(ky - y) == 3) && // 曼哈顿距离为3
(max((abs(kx - x)), abs(ky - y)) == 2) // 切比雪夫距离为2有了这两个准备工作,编程就很直接了当了。
答案

思考
不用曼哈顿距离和切比雪夫距离,也是可以解出本题的,只不过要多进行一些判定罢了。
