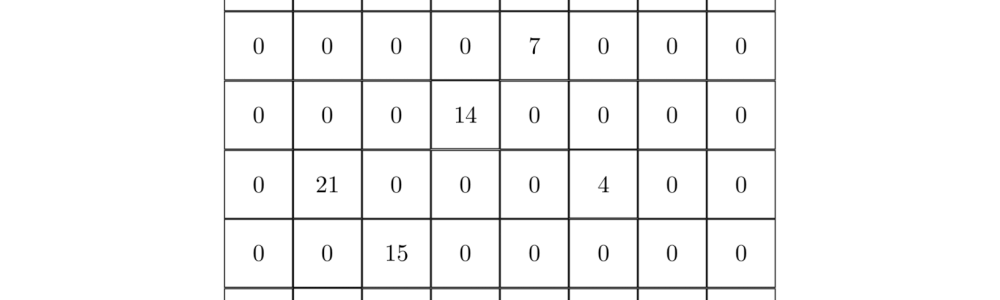
题目
分析
这是一道典型的进阶动态规划题。问题的关键是想清楚,这里的“走两次”不是独立的,而是走了一次(取走了一些数字)后再走一次。此时棋盘上有些位置已经没有数了,因此会影响DP的过程。
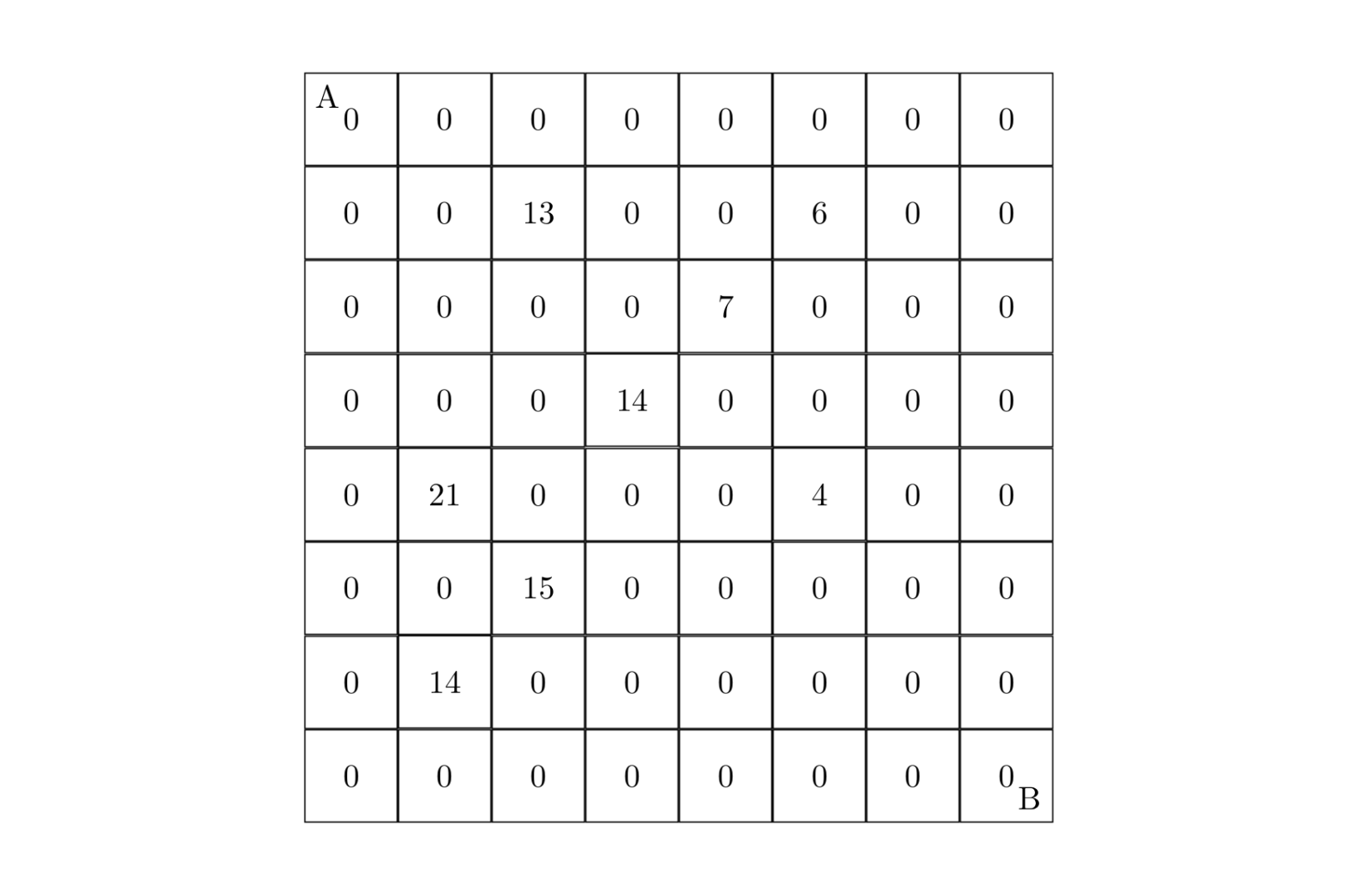
因此,这不是一个两次DP的过程,而只有一次DP,而且DP的状态转换中,必须考虑到第一次取数后的情况。如果用二维数组表示一个格子的位置(这是DP中的常规做法),那么这里要开一个四维数组。
假定考虑(i, j)(第一次取数的格子)和(k, t)(第二次取数的格子)。对于第二次取数的格子来说,它的路线不仅收到第二次取数过程的影响,也受到第一次取数过程的影响。
因此DP转移状态的时候要考虑四个方向:
- 第一次从
(i-1, j)移动到(i, j),第二次从(k-1, t)移动到(k, t); - 第一次从
(i, j-1)移动到(i, j),第二次从(k, t-1)移动到(k, t); - 第一次从
(i, j-1)移动到(i, j),第二次从(k-1, t)移动到(k, t); - 第一次从
(i-1, j)移动到(i, j),第二次从(k, t-1)移动到(k, t);
因此,(i, j)(k, t)的状态就是上述四个值的最大值加上(i, j)处的值。同时,如果这两个点不重合,那么要再加上(k, t)处的值。
最后输出[n][n][n][n]位置的值即可。
答案

思考
想通关键:虽然取了两次,但因为两次取数有关联,所以用一个DP过程解决。
本题和OJ.02.06.8786是一样的。