题目
分析
这题牵涉的数学知识不多，只有一个快速计算位数。对于\(2^P-1\)这样的数字的位数，可以用\(P\times log_{10}2+1\)快速计算——这就解决了第一问。
至于第二问，看到“500位数字”这样的要求，就知道一定要用高精度算法。注意，这里的高精度计算，涉及两部分：乘法，以及减法（最后计算-1）。
高精度乘法
乘法运算有两个核心运算：卷积以及进位。
我们手动计算乘积的时候，一般是从低到高（个位开始）在乘数中取一位，依次和被乘数的各位相乘，写下部分得数。然后将这些部分得数相加。
在用计算机模拟这个运算的时候，可以用更快一点的方式，也就是卷积。
假定有两个数：
\(A = a_0 + a_1\times 10^1 + a_2\times 10^2 + ...\)，\(B = b_0 + b_1\times 10^1 + b_2\times 10^2 + ...\)，那么它们的乘积： \(A × B = \sum_i\sum_j(a_i \times b_j \times 10^{i+j})\)。简单地说，就是：第i位和第j位相乘，得数是i*j，而“位数”是i+j。再直白一点说，就是5(00)*9(00)，得数是45，而位数是4，也就是450000。这样的好处是，我们可以一次性计算出某一个位上的得数。也就是，对于结果result[i]（第i位的得数），它一定是由a[j]*b[i-j]的总和得来。
至于进位，可以统一处理。
vector<int> multiply(const vector<int>& a, const vector<int>& b)
{
vector<int> result(MAX_DIGITS, 0);
for (int i = 0; i < MAX_DIGITS; i++)
{
for (int j = 0; j <= i; j++)
{
result[i] += a[j] * b[i - j];
}
}
// 处理进位
int carry = 0;
for (int i = 0; i < MAX_DIGITS; i++)
{
result[i] += carry;
carry = result[i] / 10;
result[i] %= 10;
}
return result;
}快速幂
在计算快速幂的时候，我们会多次计算乘法，基本算法在之前已经有描述（见P1226：快速幂（模板）），只是在此处我们要用到高精度乘法而已。这里不再单列。
答案
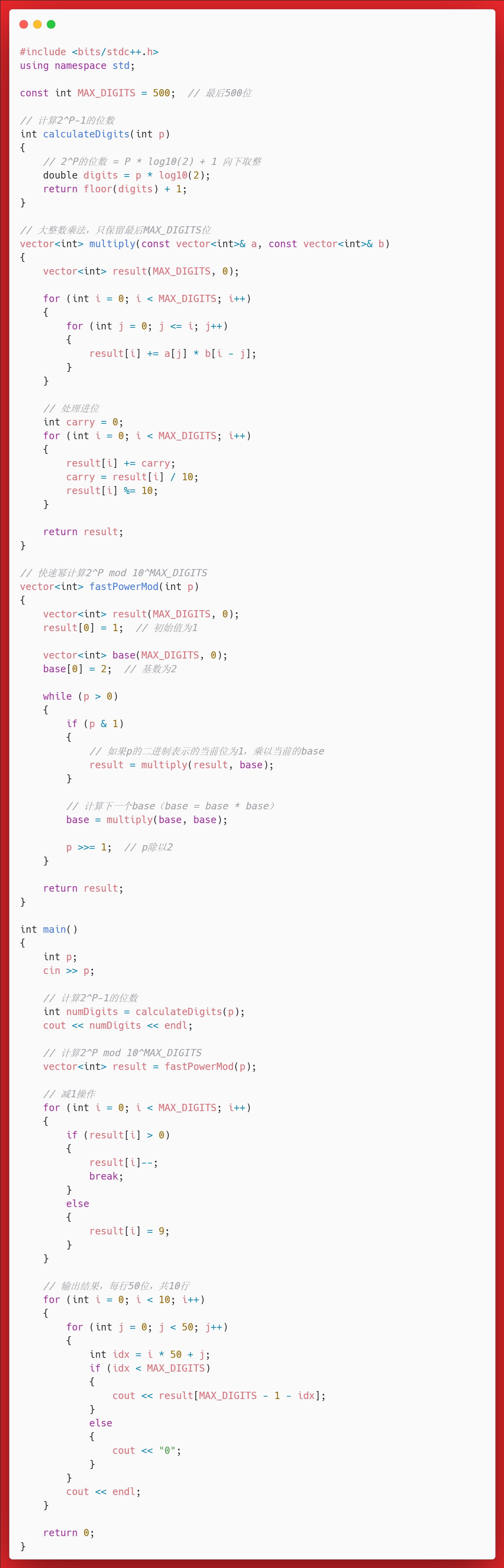
思考
这里的乘法运算用到了“卷积”的方式，而不是传统的按位计算，是一个改进。