洛谷：P1228：地毯填补问题

题目

P1228：地毯填补问题

分析

这道题目一眼可知是分治和递归的应用。但关键在于：如何分治？如何递归？

一开始，我也想错了。我的思路，是将有公主的那1/4块独立出来继续分割，直到公主所在的方块成为一个2*2的基本方块为止。而处理其它三个所谓无“障碍”方块时，需要用L形地砖填满。但是发现，L形的地砖是无法拼出一个2*2的方块的。

参考了题解后，豁然开朗。

有公主的2*2方块

如果公主在一个2*2的方块中，那么一定是可解的：

4*4方块，8*8方块，……

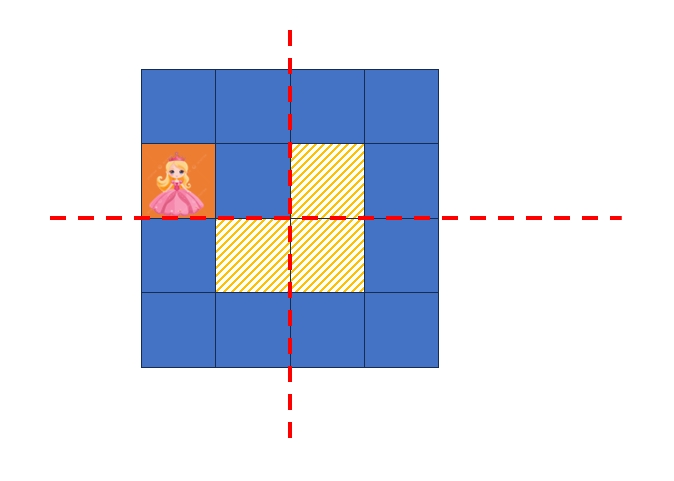
4*4的方块可以分解为4个2*2的象限。这里的洞见是，判断出公主在哪个象限后，在“原点”放一个L形地砖，为其它三个象限也各自添加一个填好的“方块”，于是：公主的位置不能放地砖=填好方块的位置不能放地砖。也就是说，相当于我们在另外三个象限也放了一个“公主”，于是问题就变成4个象限（都是2*2）都有一个“公主”，然后放L形地砖的问题。也就约简到了“有公主的2*2方块”的情形，而这个情形是可解的。（如上图所示。）

8*8方块的处理和这个相似。下图展示的，就是样本数据的填充方式：地毯一共是8*8大小（也就是\(2^3\)），公主在(3, 3)。

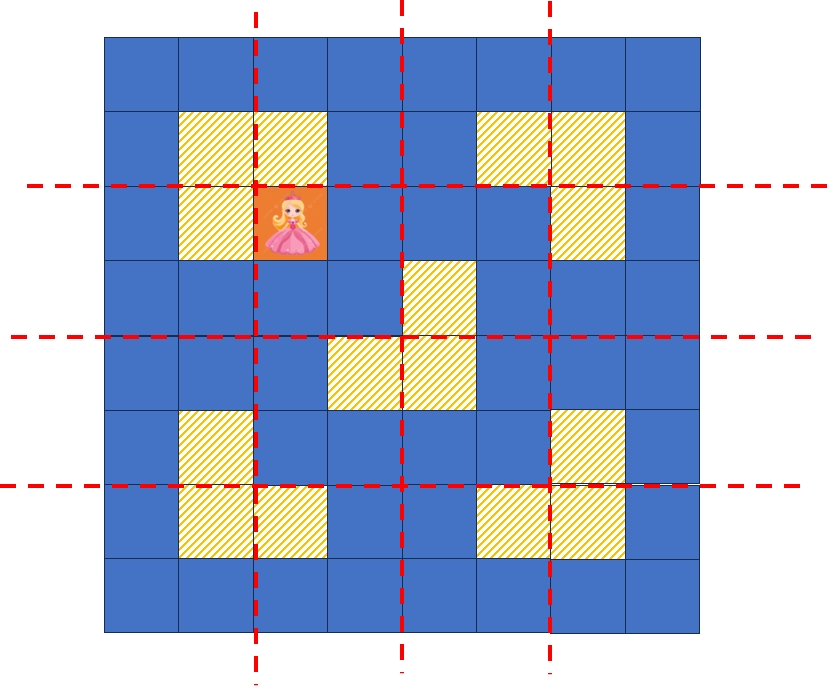
按照我们的解题思路，第一个放置的L形地砖，是类型1（缺左上角），拐点坐标是(5, 5)。因此按照输出要求是：5 5 1，与样例输出是一致的。第二个要放的L形，类型是4，拐点坐标是(2, 2)，输出是2 2 4，和样例输出一致。¹

基本算法

我们假定“公主”的坐标在\((x_1, y_1)\)，当前方格的左上角坐标是\((x_2, y_2)\)。

“公主”位置的象限判定

这个算法比较直接：

x1, y1	x2, y2	x1-x2 : n/2	y1-y2 : n/2	象限
1	1	<	<	1（左上角）
1	2	<	>	2（右上角）
2	1	>	<	3（左下角）
2	2	>	>	4（右下角）

“公主”象限确定后的处理

这里要进行几个处理。以公主在第一象限为例：

1. 中心点要放一个L形地砖，类型是1，坐标是\((x_2 + n/2, y_2 + n/2)\)。

// 特殊点在左上子棋盘，放置形状1的地毯（拐点在右下角）
cout << (x2 + (n >> 1)) << ' ' << (y2 + (n >> 1)) << ' ' << 1 << endl;

2. 递归处理更小的四个象限。

solve(x1, y1, x2, y2, (n >> 1));
solve(x2 + (n >> 1) - 1, y2 + (n >> 1), x2, y2 + (n >> 1), (n >> 1));
solve(x2 + (n >> 1), y2 + (n >> 1) - 1, x2 + (n >> 1), y2, (n >> 1));
solve(x2 + (n >> 1), y2 + (n >> 1), x2 + (n >> 1), y2 + (n >> 1), (n >> 1));

其他象限处理类似。

答案

思考

首先，建议可以按照样例，进行几次试摆后，应该就能找到分割的规律。

其次，对于递归处理四个象限时用到的几个坐标，可以用如下的图明确理解（仍然以公主在第一象限为例）：

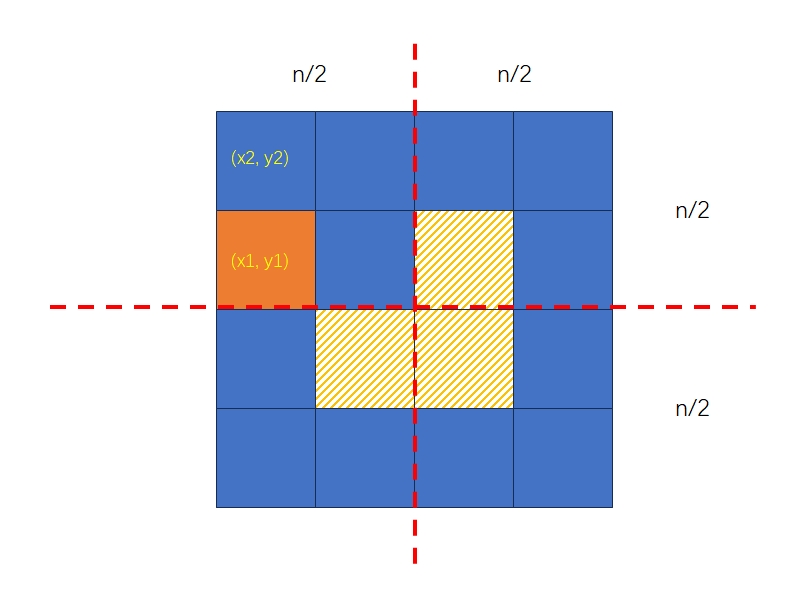
1. 第一象限递归处理：起点\((x_2, y_2)\)，特殊点\((x_1, y_1)\)，边长\(n/2\)。所以是solve(x1, y1, x2, y2, (n >> 1));。
2. 第二象限递归处理：起点\((x_2, y_2 + n/2)\)，特殊点\((x_2 + n/2 - 1, y_2 + n/2)\)，边长\(n/2\)。所以是solve(x2 + (n >> 1) - 1, y2 + (n >> 1), x2, y2 + (n >> 1), (n >> 1));。
3. 第三象限递归处理：起点\((x_2 + n/2, y_2)\)，特殊点\((x_2 + n/2, y_2 + n/2 - 1)\)，边长\(n/2\)。所以是solve(x2 + (n >> 1), y2 + (n >> 1) - 1, x2 + (n >> 1), y2, (n >> 1));。
4. 第四象限递归处理：起点\((x_2 + n/2, y_2 + n/2)\)，特殊点\((x_2 + n/2, y_2 + n/2)\)，边长\(n/2\)。所以是solve(x2 + (n >> 1), y2 + (n >> 1), x2 + (n >> 1), y2 + (n >> 1), (n >> 1));。

其他情形也是类似的。这部分也是本题最烦的地方。最稳妥的方法，是一个图一个图地画出来，然后写下坐标进行推导。