题目
分析
先看样本数据。
4 6
A<B (1)
A<C (2)
B<C (3)
C<D (4)
B<D (5)
A<B (6)这里有4个变量,6个关系。
要确定一个排序关系,就要所有的字母都确定相互关系。怎么确定相互关系呢?
我们用表格记录一下随着式子数量,这4个变量的一些特性、以及能否被确定。
(我们用0/1这样的表达表示在关系左边出现0次,右边出现1次)。
| 关系序号 | 关系 | A | B | C | D | E | F | 能否判定 |
|---|---|---|---|---|---|---|---|---|
| 1 | A<B | 1/0 | 0/1 | 0/0 | 0/0 | 0/0 | 0/0 | 否:BCD关系未定 |
| 2 | A<C | 2/0 | 0/1 | 0/1 | 0/0 | 0/0 | 0/0 | 否:BCD关系未定 |
| 3 | B<C | 2/0 | 1/1 | 0/2 | 0/0 | 0/0 | 0/0 | 否:D关系未定 |
| 4 | C<D | 2/0 | 1/1 | 1/2 | 0/1 | 0/0 | 0/0 | 可,且唯一:ABCD。 |
按照题意,能确定唯一排序后,就不用管后续输入——哪怕后续会出现矛盾的关系。
这里有几个观察:
- 根据所有关系,
A从来没有出现在右边,所以倒是第一个能确定位置的:只能在第一个。 A确定后,有些变量就能确定,那就是B:A<B才给了B一次出现在右边的机会。而现在A定位后,B只能跟在A后面出现。- 这个操作可以这样完成:
A定位后,和A相关的(B和C)出现在右边的次数要减一。 - 这样一来,
B在右边的次数为0,而C还保留了1(来自B<C的羁绊)。
- 这个操作可以这样完成:
- 因为此时
B已经不在右边,在定位的同时,可以清除和它有“羁绊”的变量。此时只有C和B关联,而且还在右边出现1次。清除这个羁绊后,C在右边也不出现,可以定位。 - 处理关系4时,
C已经定位(不再出现在右边),消去它和D的关系后,D也就可以定位了。
因此,总体算法已经有了:
- 输入,构建关系,并记录变量在右边出现的次数(“入度”)。
- 从入度为
0的元素开始定位。定位后要减少和它有关系的元素的入度。 - 重复这样的操作。直到所有元素定位。
当然,要考虑特殊情况:
- 无法定位:如果某个时刻,出现了多个入度为
0的元素,那就无法定位了——这不等于矛盾。而是信息不足,无法全部定位。 - 矛盾关系:如果处理完所有的条件,发现结果不是
n个字符,那么一定是出现了矛盾关系。这是因为,我们只将入度为0的节点放进结果。矛盾关系一定是一个环的关系:比如A<B, B<C, C<A这样的。因为存在环,所以入度不会为0,也就进不了最后结果,也就造成结果的长度不会等于n(个变量)。
答案
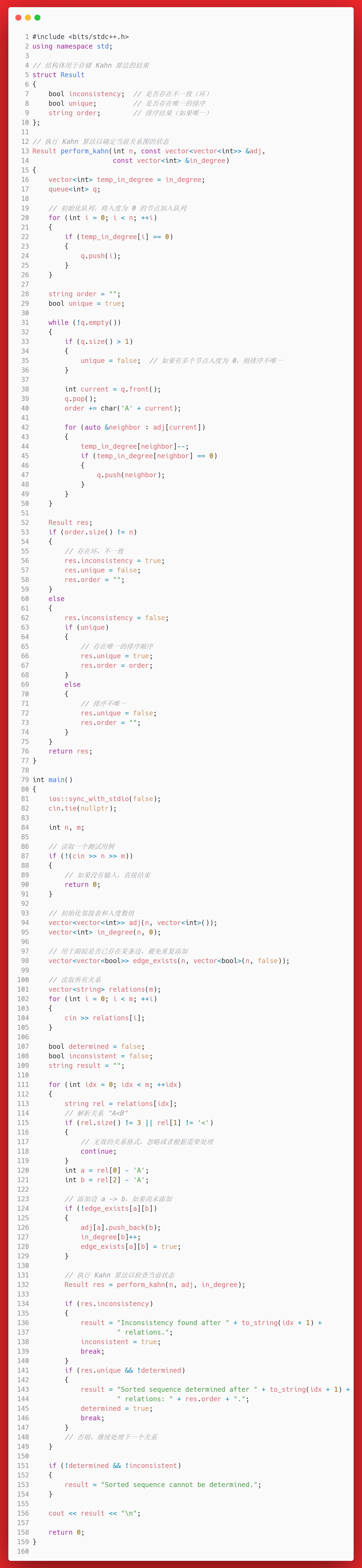
思考
这是一个模拟拓扑排序的过程。
如果:
- 左边出现次数类似于出度:表示这个字母比多少字母大
- 右边出现次数类似于入度:表示有多少字母比这个字母大
- 当一个字母的右边出现次数为0时,就像入度为0一样,可以确定它的位置
因此,算法的过程就是在模拟拓扑排序。不过,此处我们只要统计次数即可。
