题目
分析
这道题,关键是想通两个公式:
- 如果以任意一点作为设置医院的点,那么到这个点(“医院”)的所有点有四个方向:左子树,右子树,父节点,以及自己。换句话说,到这一点的总开销来自这四个方向的开销的总和。
- 如果某个节点到“医院”的距离是
d,那么它的四个方向的点的距离是d+1。
当然,如果我们从一个点跑到某个子树点,那么这个子树点的父节点就是原来那个点,在计算费用的时候不能重复,所以还要有个数组记录某个点是否已经被访问。
从上述描述可以看出,这是一个暴力+DFS的算法:首先遍历各个可能作为“医院”的节点,然后从这个节点开始DFS四个“方向”:左、右、父、自己。不断比较“费用”,保留最小的那个就是答案。
答案

思考
首先,这个题目中的节点结构有一点不同,它不止保留了父到子的方向,而且保留了另一个“子->父”的方向,这是为了遍历的方便。这个做法是最直接的,而且代码量很少。
其次,这个题目还可以用BFS+邻接表(无向图)的算法实现。大致步骤是:
- 使用邻接表表示树的结构
- 采用 BFS 而不是 DFS 来计算距离
- 对每个可能的医院位置,计算到所有其他节点的最短距离
- 使用队列确保距离计算的正确性
代码如下。
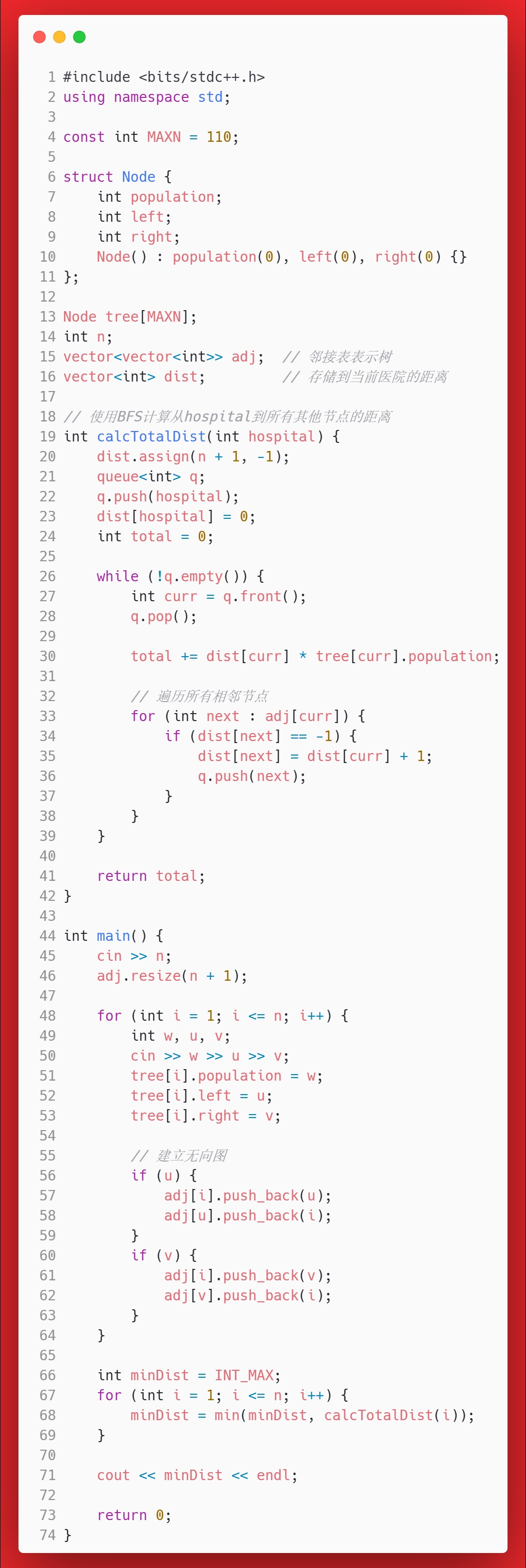
这个BFS的算法也很简明,但需要借助一些辅助的数组(adj是一个记录了相邻关系的数组)。
