洛谷：P1525：关押罪犯


洛谷：P1525：关押罪犯

Table of Contents

题目

P1525：关押罪犯

分析

这是一道很好的题目，因为结合了贪心和并查集。

按照题意，很显然的一点是：相互间仇恨度越高的两个罪犯要分配到两个不同的监狱。这个过程有两个终止的状态：

  1. 所有的冲突关系都能“妥善”处理——也就是这两个罪犯都可以分配到两个监狱中去。而且，不存在传递关系，比如：1-2、2-3，4-5。这时，5个罪犯可以分在两个监狱，而不发生冲突。
    1. 冲突发生的条件是，出现了“敌人的敌人”，因为这个“敌人的敌人”不能和敌人关在一起，只能和自己关在一起。无论这个敌人的敌人是否和自己有冲突关系，我们都能得到较小的冲突值。
    2. 只要不发生冲突，我们可以处理完所有的仇恨关系。如果我们用循环变量在1~m之间处理给出的m对关系，那么最后循环变量会是m+1。
  2. 假定按照仇恨度降序，出现仇恨关系是1-2、2-3，1-3，这时出现了仇恨的传递和“咬合”。只能将3分到1所在监狱才会更好。但出现这种情况后，不用再继续了，因为1-3的冲突不可避免，也就是我们能找到的最小的最大冲突。后续可能存在的冲突只会更小，已经不符合题目的要求。

上面的第二点，是不是很有意思？其实就是P01892中提到的“敌人的敌人就是朋友”的关系的变形。这是本题中贪心算法和使用并查集的基础。

让我们用样本数据来详细说明一下。给出的冲突关系是：

4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884

由于4个囚犯之间最多有6个仇恨关系，所以会落到上述讲到的第二种终止状态。

先将仇恨值按照降序排列，得到：

1 2 28351
3 4 12884
1 3 6618
2 3 3512
1 4 2534
2 4 1805

首先，每个囚犯的“祖先”都是自己，表明目前属于各个不同的监狱（一共4个——这当然是不对的）。

  1. 1-2因为祖先不同，所以分属两个监狱。只要更新记录1-2之间有关联——2的祖先是1。
  2. 3-4处理方式同上。4的祖先是3。它们具体各自在哪个监狱无所谓，因为也不会成为最终的答案。
  3. 1-3也应该分开。不管上一步怎么分配3/4，总能让1/3在不同的监狱。但此时要更新3的祖先也是1。
  4. 2-3的情况有意思了：2的祖先是1，3的祖先也是1。这说明2和3只能被分在同一监狱，而它们之间的仇恨值是3512。这个冲突无法避免。

到这里就可以停止了，因为我们已经发现了一个无法避免的冲突：在此之前的冲突值虽然更大，但由于在两个监狱，最终不会发生冲突，而在这个之后的冲突值只会越来越小。所以3512就是最小的最大仇恨值。后面的1-4和2-4都不需要继续处理了。

总结一下就是：每次都进行溯源和归并，在发现祖先是同一个后，直接终止。

答案

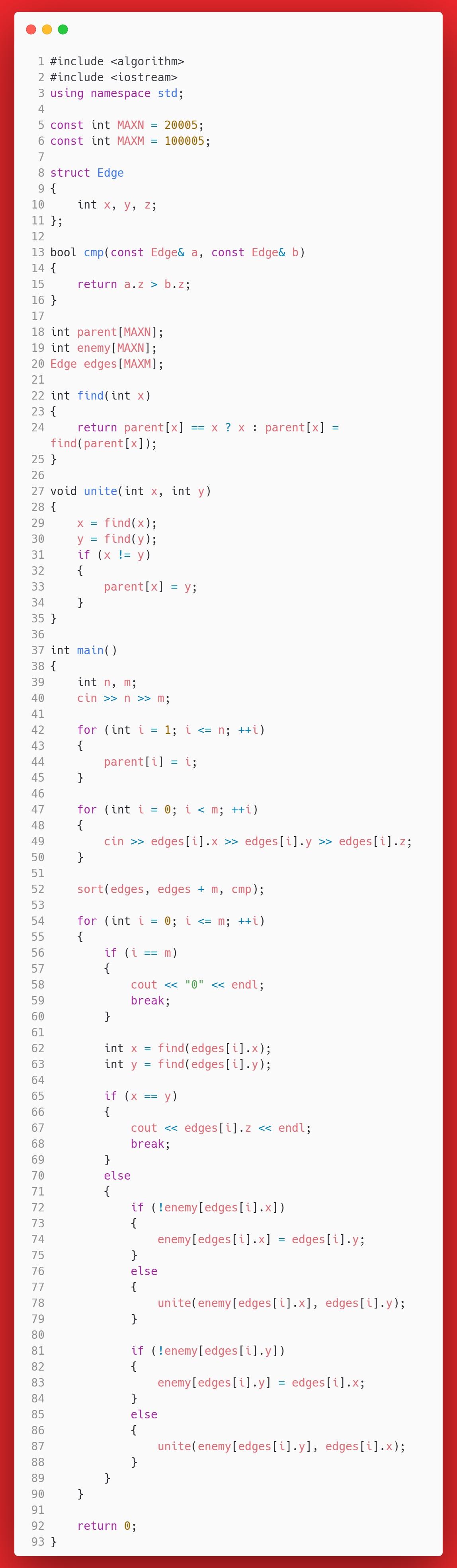
思考

这道题的关键，是想明白：

  1. 通过降序排列仇恨度，总能找到最大的最小仇恨度。因为一旦冲突无法避免，我们总是找到了一个较小的最大值。
  2. 一旦出现自己的敌人的敌人，那么自己和“敌人的敌人”在一起，总能降低最大的仇恨度。因为此时要么自己和敌人的敌人没有仇恨，要么这个仇恨度也小于“自己的敌人”和“敌人的敌人”的仇恨度——这点由1中的排序保证了。

另外，如果我们有三个监狱，又该如何处理？

上一篇 下一篇