洛谷：P1551：亲戚

题目

P1551：亲戚

分析

题目中提到的“亲戚”关系可以进一步抽象，比如“从属”、“关联”、“代表”等，因此有着很重要的应用。

从属关系的存储

最简单的，是用数组来表示这样的从属关系，由于“父子”关系是一对多的，所以应该用“子”作为数组的索引，而“父”作为其值。比如：

parents[son] = father;

表示son的“父辈”是father。

找到最终代表

考虑一下的关系图：

很明显，除了节点6之外，其他节点之间都有所谓的“亲戚”关系：因为在图中可以看出节点1充当了节点1/2/3/4/5的共同“父辈”。

当然，和现实中不同，这里的“父辈”可以是任意节点。例如，节点3也可以成为最终的“父辈”。

两个节点是否存在“亲戚”关系当且仅当两个节点有一个共同的最终父辈。我们可以定义一个函数来找到某节点的最终父辈：

int find(int s)
{
    if (s == parents[s])
    {
        return s;
    }
    return parents[s] = find(parents[s]);
}

这是一个通过递归找到最终父辈的代码。这里的reutrn一行，我们稍后解释。

“祖先”的归并

并查集更关注的是一些节点是否在一个“组”（“家族”）中。

因此，这里的归并不完全代表了一种“从属”关系，可能用“关联”、“代表”更贴切。也因此，在编程时，到底哪个节点成为代表无所谓，只要一个“家族”只有一个统一的代表即可。

对于两个不同的节点s和t，我们先找到它们各自的最终父辈，如果不同，则将其中一个的父辈设置为另一个即可。

void merge(int s, int t)
{
    s = find(s);
    t = find(t);
    if (s != t)
    {
        parents[s] = t;
    }
}

答案

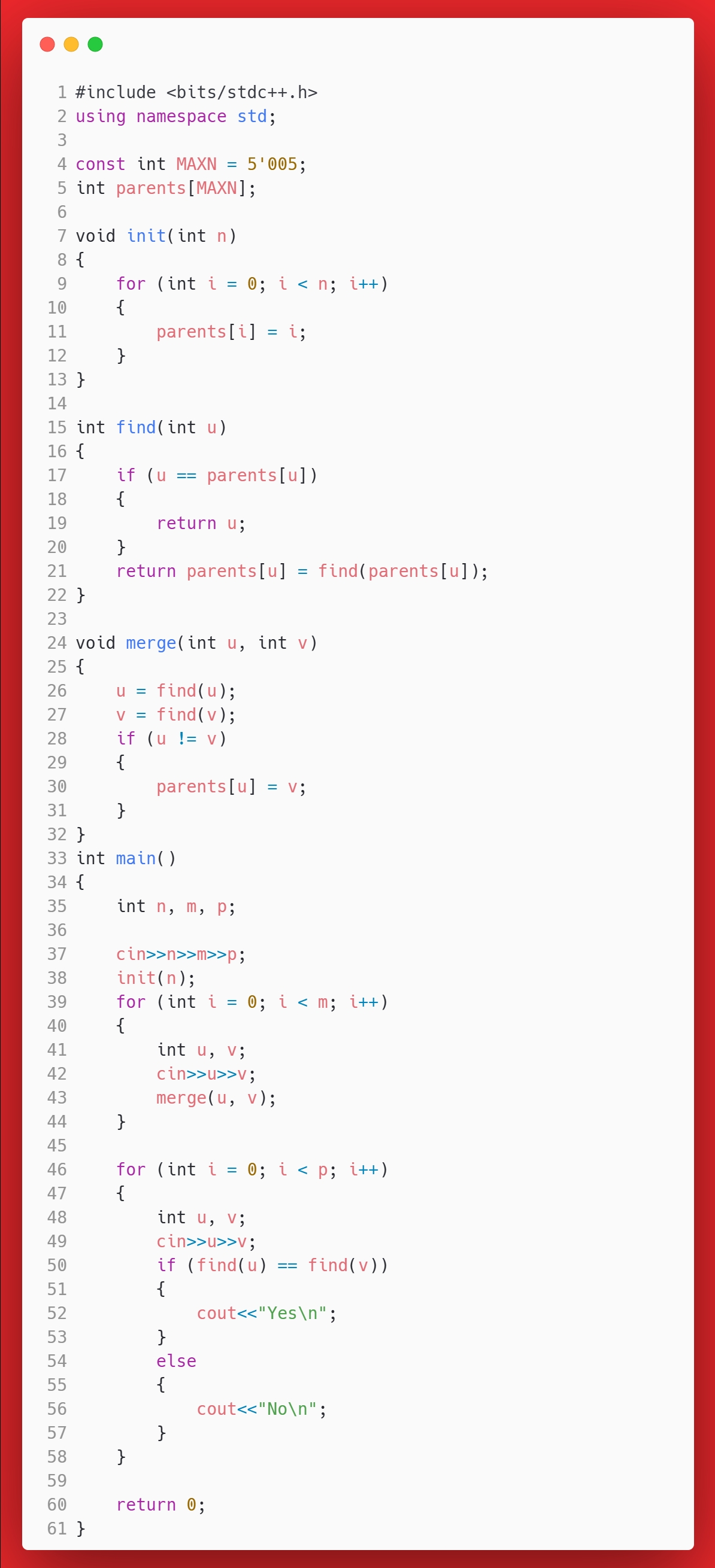
思考

这里，对上文代码中find函数中的最后一行做个解释：

int find(int s)
{
    if (s == parents[s])
    {
        return s;
    }
    return parents[s] = find(parents[s]);
}

并查集有一个问题：如果我们保持parents[s]=f的设置，有可能出现一个很长的“链条”：s->t->u->v->w->x->y...。这样一来，从s开始的查找最后父辈就会经过一个很长的链条。因此，我们可以“压扁”整个路径：将所有路径上的节点的“父”节点都设置为最终的那个最终父辈节点。最后这一行return parents[s] = find(parents[s]);就是完成这个任务。