题目
分析
这道题是明确的:根据前序遍历和中序遍历,得到后续遍历。属于基本概念题。
假定有如下的一棵二叉树:
前序遍历
前序遍历按照“根-左-右”的顺序进行。以上图为例,遍历顺序就是1-2-3-4-5-6-7。
中序遍历
中序遍历按照“左-根-右”的顺序进行。以上图为例,遍历顺序就是4-3-5-2-6-1-7。
后序遍历
后序遍历按照“左-右-根”的顺序进行。以上图为例,遍历顺序就是4-5-3-6-2-7-1。
本题是根据中序+前序,要求出后序。
从前序定义得知:它最早访问的就是根节点;从中序定义来看,根节点分割了左右子树。
在中序中找到“根节点”的位置,可以将中序遍历分成“左-根-右”三个部分,然后按照后序遍历的顺序,递归构建“左-右-根”。
这就是本题的解题关键。
请见下表的说明。
| 步骤 | 前序序列 | 中序序列 | 后序构建过程 | 说明 |
|---|---|---|---|---|
| 1 | 1-2-3-4-5-6-7 | 4-3-5-2-6-1-7 | _ | 根节点是1,中序中1左边是(4-3-5-2-6),右边是(7) |
| 2 | 2-3-4-5-6 | 4-3-5-2-6 | _ | 处理左子树:根节点是2,左边是(4-3-5),右边是(6) |
| 3 | 3-4-5 | 4-3-5 | _ | 处理左子树:根节点是3,左边是(4),右边是(5) |
| 4 | 4 | 4 | 4 | 最左叶子节点,直接加入后序 |
| 5 | 5 | 5 | 4-5 | 处理3的右子树,加入后序 |
| 6 | - | - | 4-5-3 | 处理完3的左右子树,将3加入后序 |
| 7 | 6 | 6 | 4-5-3-6 | 处理2的右子树,将6加入后序 |
| 8 | - | - | 4-5-3-6-2 | 处理完2的左右子树,将2加入后序 |
| 9 | 7 | 7 | 4-5-3-6-2-7 | 处理1的右子树,将7加入后序 |
| 10 | - | - | 4-5-3-6-2-7-1 | 处理完1的左右子树,将1加入后序 |
最终得到后序遍历序列:4-5-3-6-2-7-1
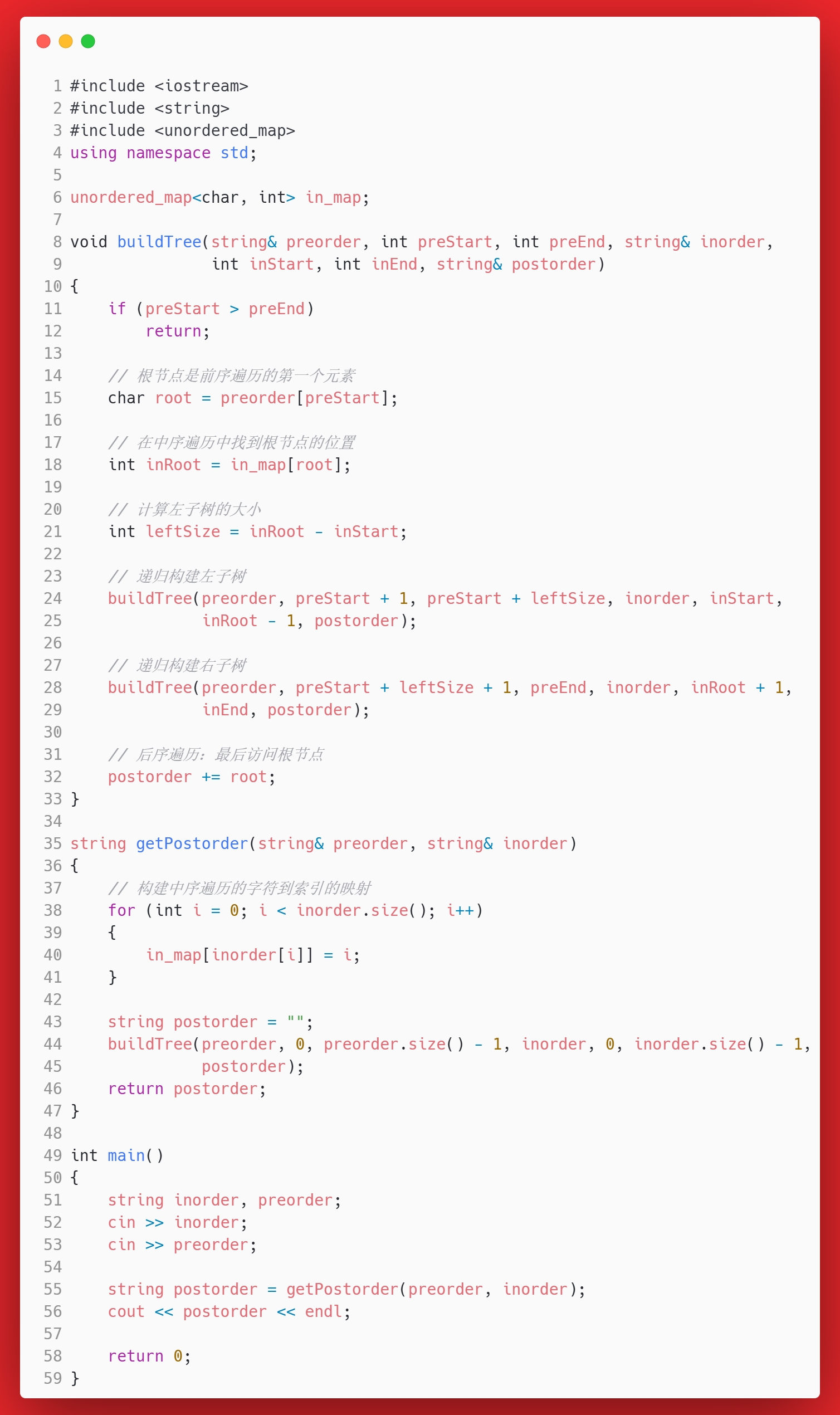
有了这个过程,就可以写出相应的代码:
void buildTree(string& preorder, int preStart, int preEnd, string& inorder, int inStart, int inEnd, string& postorder)
{
if (preStart > preEnd)
{
return;
}
// 根节点是前序遍历的第一个元素
char root = preorder[preStart];
// 在中序遍历中找到根节点的位置
int inRoot = in_map[root];
// 计算左子树的大小
int leftSize = inRoot - inStart;
// 递归构建左子树
buildTree(preorder, preStart + 1, preStart + leftSize, inorder, inStart, inRoot - 1, postorder);
// 递归构建右子树
buildTree(preorder, preStart + leftSize + 1, preEnd, inorder, inRoot + 1, inEnd, postorder);
// 后序遍历:最后访问根节点
postorder += root;
}这个递归函数的核心点就是:根据前序遍历的性质,找到根节点,分成左右两棵子树,然后分别计算大小。然后递归构建。注意构建的顺序要按照后序遍历的“左-右-根”顺序来,所以最后加上根节点。
这里有一个辅助数组,用来快速查找前序遍历中各个节点在中序遍历中的位置。
假定输入的内容是:
(前序):ABEDFCHG
(中序):CBADEFGH
那么构建的in_map数组内容如下(按前序遍历顺序排列):
| 前序中的字符(按访问顺序) | A | B | E | D | F | C | H | G |
|---|---|---|---|---|---|---|---|---|
| 该字符在前序中的位置 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 该字符在中序中的位置 | 2 | 1 | 4 | 3 | 5 | 0 | 7 | 6 |
这样,当我们需要在中序遍历中查找某个字符的位置时,可以直接通过in_map数组O(1)时间得到。例如:
in_map['A'] = 2表示根节点A在中序遍历中位于第2个位置,也就将中序分为左子树(0-1)和右子树(3-7)。in_map['C'] = 0表示C在中序遍历中位于第0个位置,是左子树的最左节点。
这棵树的完整构造应该是:
后续遍历正好是AEFDBHGC。
答案
思考
我们已经根据前序+中序,得到了后序。那么自然的问题就是:这三种遍历方式,是否都可以根据其中两个得到第三个呢?
回答是:
- 给出前序+后序,无法确定中序。
- 给出中序+后序,可以确定前序。
代码如下:1
#include <iostream>
#include <string>
#include <unordered_map>
using namespace std;
unordered_map<char, int> in_map;
void buildTree(string& postorder, int postStart, int postEnd, string& inorder,
int inStart, int inEnd, string& preorder)
{
if (postStart > postEnd)
return;
// 根节点是后序遍历的最后一个元素
char root = postorder[postEnd];
// 将根节点加入前序遍历
preorder += root;
// 在中序遍历中找到根节点的位置
int inRoot = in_map[root];
// 计算左子树的大小
int leftSize = inRoot - inStart;
// 递归构建左子树
buildTree(postorder, postStart, postStart + leftSize - 1, inorder, inStart,
inRoot - 1, preorder);
// 递归构建右子树
buildTree(postorder, postStart + leftSize, postEnd - 1, inorder, inRoot + 1,
inEnd, preorder);
}
string getPreorder(string& postorder, string& inorder)
{
// 构建中序遍历的字符到索引的映射
for (int i = 0; i < inorder.size(); i++)
{
in_map[inorder[i]] = i;
}
string preorder = "";
buildTree(postorder, 0, postorder.size() - 1, inorder, 0, inorder.size() - 1, preorder);
return preorder;
}
int main()
{
string inorder, postorder;
cin >> inorder >> postorder;
string preorder = getPreorder(postorder, inorder);
cout << preorder << endl;
return 0;
}可以发现,基本代码和例题差不多。但有两个重要的不同:
- 首先,后序遍历的最后一个节点是根节点。并由此在中序中进行分割。
- 其次,前序遍历的特点是先访问根节点,所以根节点的追加在递归之前。
书上的例题还有一道16-10,也明确地说明了只有前序和后序的话,中序遍历是不唯一确定的。并且给出了一个一个判定:
如果前序中出现
AB,而后序中出现BA,那么这个节点一定只有一个儿子。而一旦出现x个这样的节点,那么根据乘法原理,每个这样的节点可能有左节点或者右节点两种可能性,所以影响到最终的中序遍历有\(2^x\)种可能。这里不再赘述。
-
这个代码也是洛谷P1030:求先序排列的AC代码。 ↩
