题目
分析
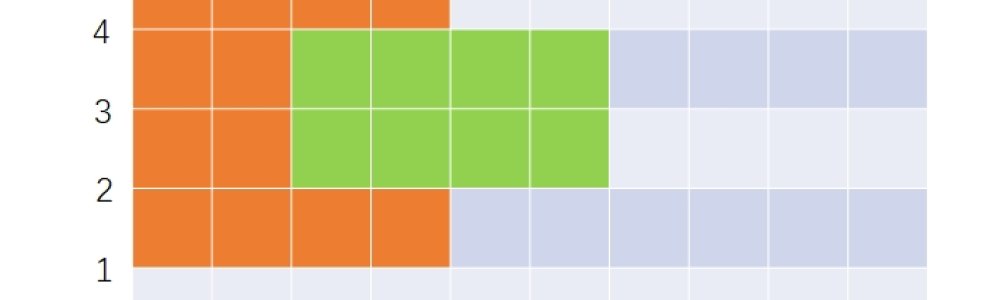
先分析样本数据。根据样本数据,可以画出两个矩形如下。
- 第一个矩形坐标:
(0, 5) - (4, 1)(橙色)。面积16。部分会被第二个矩形遮盖(重合)。 - 第二个矩形坐标:
(2, 4) - (6, 2)(绿色)。面积8。 - 重合部分面积为4。最终面积:
16+8-4=20。
但是,我们在真正计算的时候,不能这么算。重合的矩形计算很烦,何况还有多个矩形多重重合的情形。
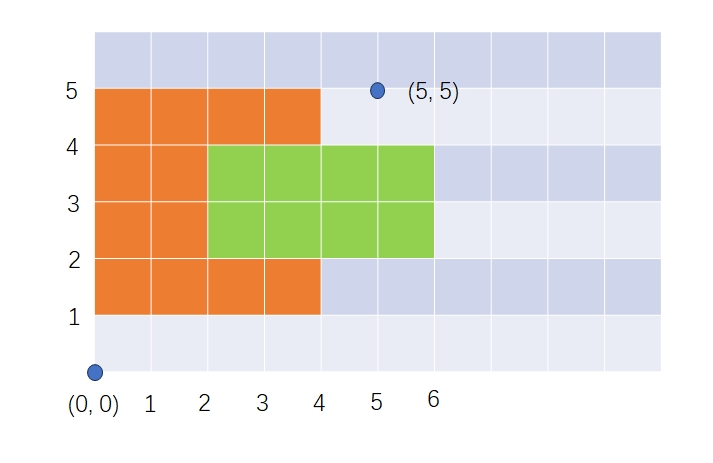
我们换一个思路:整理所有的x和y坐标并加以排序,得到:
x: 0 2 4 6
y: 1 2 4 5去重排序后x有k=4个端点,y有m=4个端点。相邻端点两两一组产生k-1=3个x段(\([0,2],[2,4],[4,6]\)),m-1=3个y段(\([1,2],[2,4],[4,5]\))。两个方向的段相乘得到9个小格。
每个小格的定义为\([x_i, x_{i+1}] × [y_j, y_{j+1}]\),面积为\((x_{i+1}-x_i) \times (y_{j+1}-y_j)\)。只要某个小格被任意一个原始矩形完全包含,就把该小格面积加到答案——按小格累加可以正确处理任意层数的重叠且不会重复计数。
下面列出全部9个小格,并说明是否被原矩形完全包含(R1 = (0,1)-(4,5),R2 = (2,2)-(6,4)):
| 编号 | 小格(左,下)-(右,上) | 宽×高 | 面积 | 是否被原矩形完整包含 |
|---|---|---|---|---|
| 1 | (0,1)-(2,2) | 2 × 1 | 2 | 是(被 R1) |
| 2 | (0,2)-(2,4) | 2 × 2 | 4 | 是(被 R1) |
| 3 | (0,4)-(2,5) | 2 × 1 | 2 | 是(被 R1) |
| 4 | (2,1)-(4,2) | 2 × 1 | 2 | 是(被 R1) |
| 5 | (2,2)-(4,4) | 2 × 2 | 4 | 是(被 R1 与 R2) |
| 6 | (2,4)-(4,5) | 2 × 1 | 2 | 是(被 R1) |
| 7 | (4,1)-(6,2) | 2 × 1 | 2 | 否 |
| 8 | (4,2)-(6,4) | 2 × 2 | 4 | 是(被 R2) |
| 9 | (4,4)-(6,5) | 2 × 1 | 2 | 否 |
把被包含的小格面积相加得到:\(2+4+2+2+4+2+4 = 20\),与样例结果一致。
剩下的问题就是如何判定这个某个小格子是否被完全覆盖在原来的某个矩形中。这个算法不难。
核心代码如下:
for (int i = 0; i < x_discrete.size() - 1; i++)
{
for (int j = 0; j < y_discrete.size() - 1; j++)
{
//两两配对,获得小格子左下(left, bottom)以及右上(right, top)的坐标
long long left = x_discrete[i];
long long right = x_discrete[i + 1];
long long bottom = y_discrete[j];
long long top = y_discrete[j + 1];
// 检查这个小矩形是否被任何输入矩形覆盖
bool covered = false;
for (const auto& rect : rectangles)
{
// 矩形覆盖条件:左上角(x1,y1),右下角(x2,y2)
// 小矩形在大矩形内部的条件
if (rect.x1 <= left && right <= rect.x2 && rect.y2 <= bottom &&
top <= rect.y1)
{
covered = true;
break;
}
}
if (covered)
{
total_area += (right - left) * (top - bottom);
}
}
}辅助函数
- 离散化函数
discretize
利用STL,我们可以非常快地排序、去重:
vector<long long> discretize(const vector<long long>& coords)
{
vector<long long> sorted_coords = coords;
sort(sorted_coords.begin(), sorted_coords.end());
// 去除重复元素:先用unique()将重复元素移到末尾,再用erase()删除
// 使用unique()函数将相邻的重复元素移动到容器末尾,返回指向第一个重复元素的迭代器
auto new_end = unique(sorted_coords.begin(), sorted_coords.end());
// 使用erase()函数删除从new_end到容器末尾的所有重复元素
sorted_coords.erase(new_end, sorted_coords.end());
return sorted_coords;
}答案

思考
这个代码可以通过洛谷的提交,但时间复杂度较高(\(O(n^3)\))。
改进方法一:不再遍历所有矩形,而是改用标记法。标记法前面几步和原来的方法一致:需要获得所有坐标的离散化数组(x_discrete和y_discrete)。
我们不再对坐标范围标记“覆盖”,而是对这个范围的位置进行标记。
// 标记矩形覆盖的所有网格
// 注意:y坐标系中y1 > y2(左上角到右下角)
for (int i = x1_idx; i < x2_idx; i++)
{
for (int j = y2_idx; j < y1_idx; j++)
{
covered[i][j] = true;
}
}这比标记数值范围要少很多操作。
在计算面积时,我们只加总被覆盖的区域:
long long total_area = 0;
for (int i = 0; i < x_size - 1; i++)
{
for (int j = 0; j < y_size - 1; j++)
{
if (covered[i][j])
{
long long width = x_discrete[i + 1] - x_discrete[i];
long long height = y_discrete[j + 1] - y_discrete[j];
total_area += width * height;
}
}
}我们不再重复判定某个小格子是否在原来的矩形覆盖范围内——这已经一次性由covered数组标记。