题目
分析
这道题目和P4147:玉蟾宫非常相像,不过后者是求面积,这里是求可以切割出的矩形的计数。这会造成一些小小的差异。
确定高度
我们设置一个全局变量heights[i][j]去存储:对于格子(i, j),它的高度。这个高度是后续单调栈找左右边界时的核心。
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (grid[i][j] == '*') // *表示用过了,或者说障碍
{
heights[i][j] = 0;
}
else
{
heights[i][j] = heights[i - 1][j] + 1;
}
}
}单调栈确定左右边界
用单调栈来确定格子(i, j)由于相应高度限制而能到达的左右边界。这里和P4147:玉蟾宫开始出现细微的差异,体现在左右边界的判定上。
先讨论两个例题中左边界的计算。
//4147中的计算
for (int j = 0; j < m; ++j)
{
while (!s.empty() && heights[i][s.top()] >= heights[i][j])
{
s.pop();
}
left[j] = s.empty() ? 0 : s.top() + 1;
s.push(j);
}其逻辑是:只要栈顶的高度不小于当前的高度,就表明可以继续往左拓展(也就是画出的矩形的左边界可以往左)。而一旦小于当前高度,j列的左边界拓展就戛然而止,因此此时的左边界是栈顶+1。
//1950中的计算
for (int j = 1; j <= m; j++)
{
while (!s.empty() && heights[i][s.top()] >= heights[i][j])
{
s.pop();
}
if (s.empty())
{
left_border[j] = 0;
}
else
{
left_border[j] = s.top();
}
s.push(j);
}它的额逻辑和4147基本类似,但是左边界不用+1。这体现在后续的面积计算上。
在计算右边界的时候:
//4147中的计算
for (int j = m - 1; j >= 0; --j)
{
while (!s.empty() && heights[i][s.top()] >= heights[i][j])
{
s.pop();
}
right[j] = s.empty() ? m : s.top();
s.push(j);
}右边界是最后一个不低于j列高度的单元格,和题目要求一致。
//1950中的计算
for (int j = m; j >= 1; j--)
{
while (!s2.empty() && heights[i][s2.top()] > heights[i][j])
{
s2.pop();
}
if (s2.empty())
{
right_border[j] = m + 1;
}
else
{
right_border[j] = s2.top();
}
s2.push(j);
}注意heights[i][s2.top()] > heights[i][j]这里用到了>而不是>=。
总结一下,在本题中:
- 左边界使用
>=确保相同高度的列只有最左边的那个会被计算。 - 右边界使用
>确保相同高度的列只有最右边的那个会被计算。
这种不对称处理确保了每个可能的矩形只被计算一次,避免了重复计算,对本题这种需要计算所有可能矩形数量的问题非常关键。
划分矩形数量
从(i, j)这个格子出发,高度有heights[i][j]中选择,向左有j-left_border[j]种选择,向右有right_border[j]-j种选择。所以总的方式是:\(ans+=heights[i][j]\times(right\_border[j]-j)\times(j-left\_border[j]);\)
答案
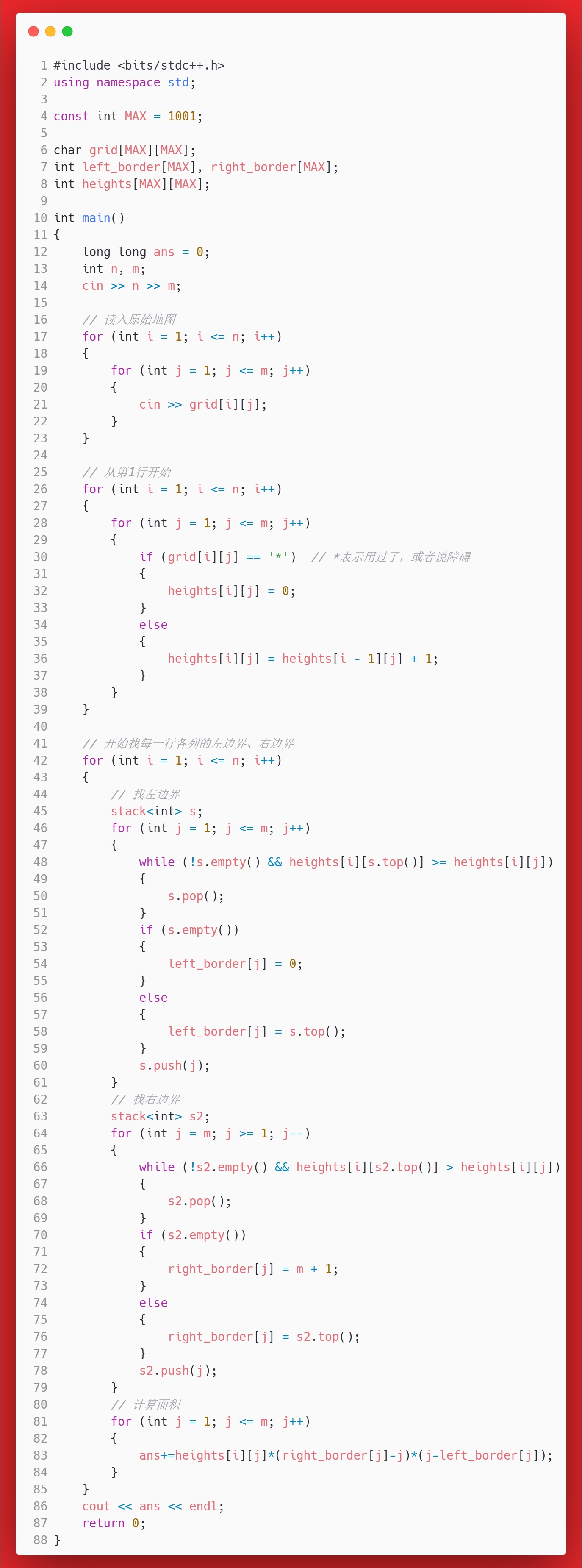
思考
(略)
