题目
分析
这道题不像描述中看起来的那么简单,因为虽然我们可以轻易看出这是一道DP的题目,但是状态转换非常繁琐。需要一一甄别。
首先,是合理的假定:对于2*N的墙壁,我们从左到右进行覆盖,在覆盖到i列的时候,前i-1列不会有没有未曾覆盖的地方,而i列之后的也不会有任何被覆盖的地方。
其次,因此,i列的状态是需要进行研究的。一共有四种可能的状态,分别记作0/1/2/3。而这几个状态,是可以从前一列的状态转移过来的。
第三,因此,我们应该根据上述转移方式来编写核心的DP状态转移方程。
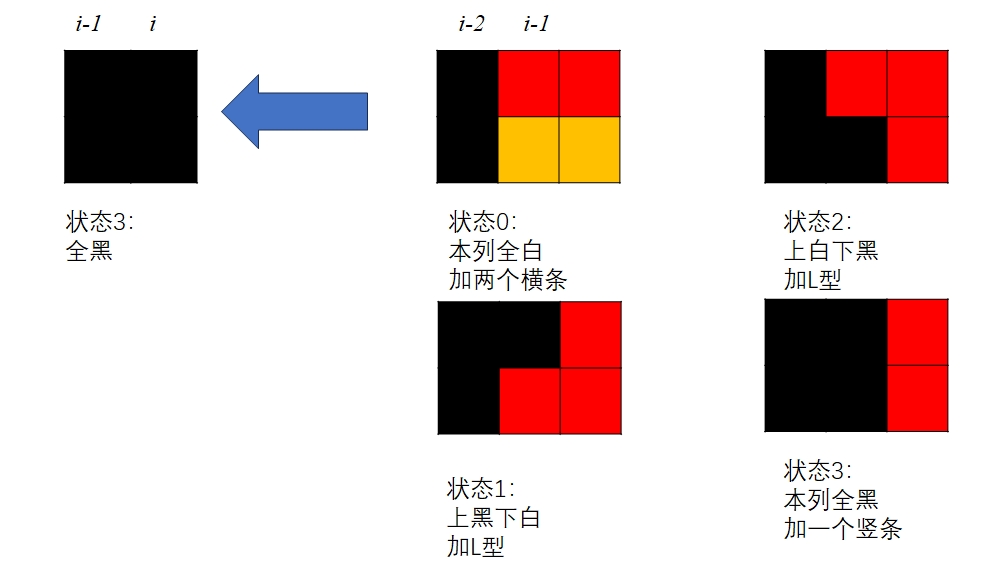
四种状态的定义
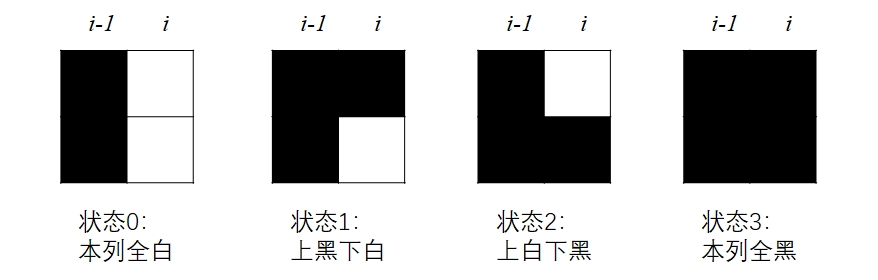
以及转移
我们定义dp[i][0/1/2/3]分别对应了i列与上面定义一一对应的4种状态。
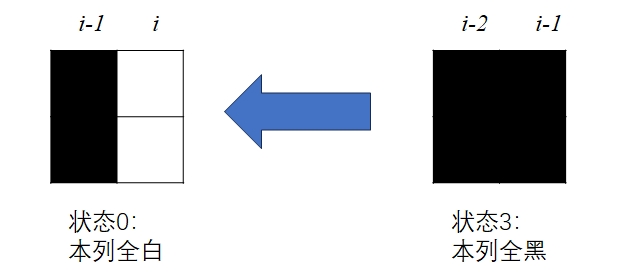
dp[i][0]实际上就是dp[i-1][3],亦即:\(dp[i][0]=dp[i-1][3]\)。
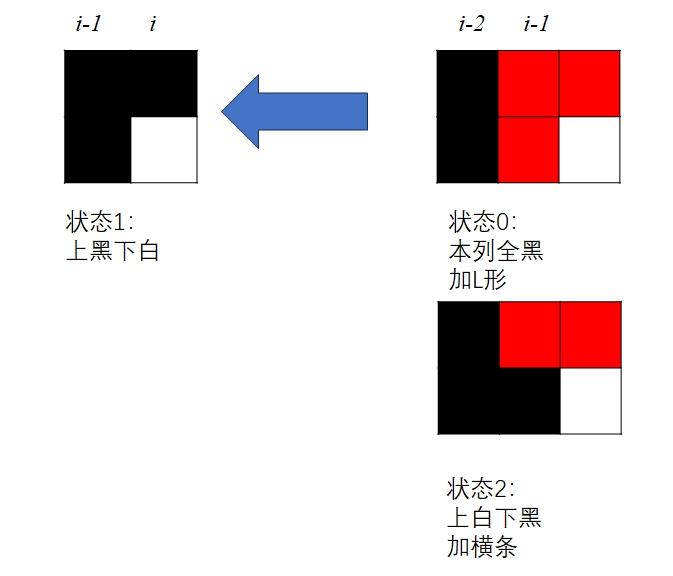
dp[i][1]可以来自两个状态:i-1处于0状态(全白),然后加一个L形;或者i-1处于2状态(上白下黑),然后加一个横条。因此:\(dp[i][1]=dp[i-1][0]+dp[i-1][2]\)。
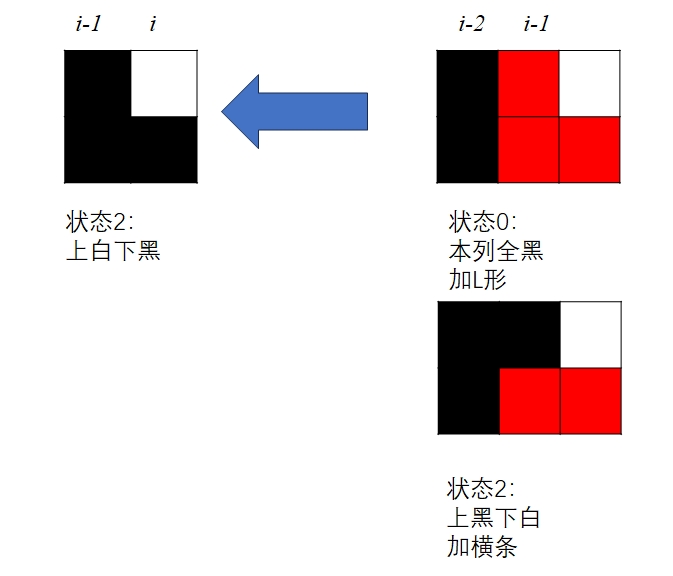
dp[i][2]可以来自两个状态:i-1处于0状态(全白),然后加一个L形;或者i-1处于1状态(上黑下白),然后加一个横条。因此:\(dp[i][2]=dp[i-1][0]+dp[i-1][1]\)。
-
dp[i][3]可以来自更多状态:i-1处于0状态(全白),那么要加两个横条。\(dp[i][3]=dp[i-1][0]\)。这里不用加竖条——想想为什么?i-1处于1状态(上黑下白),那么要加一个L形。\(dp[i][3]=dp[i-1][1]\)。i-1处于2状态(上白下黑),那么要加一个L形。\(dp[i][3]=dp[i-1][2]\)。i-1处于3状态(全黑),那么要加一个竖条。\(dp[i][3]=dp[i-1][3]\)。这里可以回答4.1中的问题,因为加两个竖条的情形归并到了这种情形。
最后到了第N列,因为必须全部铺满,所以必然处于3状态:\(dp[N][3]\)。
初始条件是什么呢?\(dp[0][3]=1\)。
其他的代码就很简单了。
答案

思考
这是一道有一定难度的DP题目,要点就在于分析清楚各列从前一列转移过来的不同情形。
