Table of Contents
题目
分析
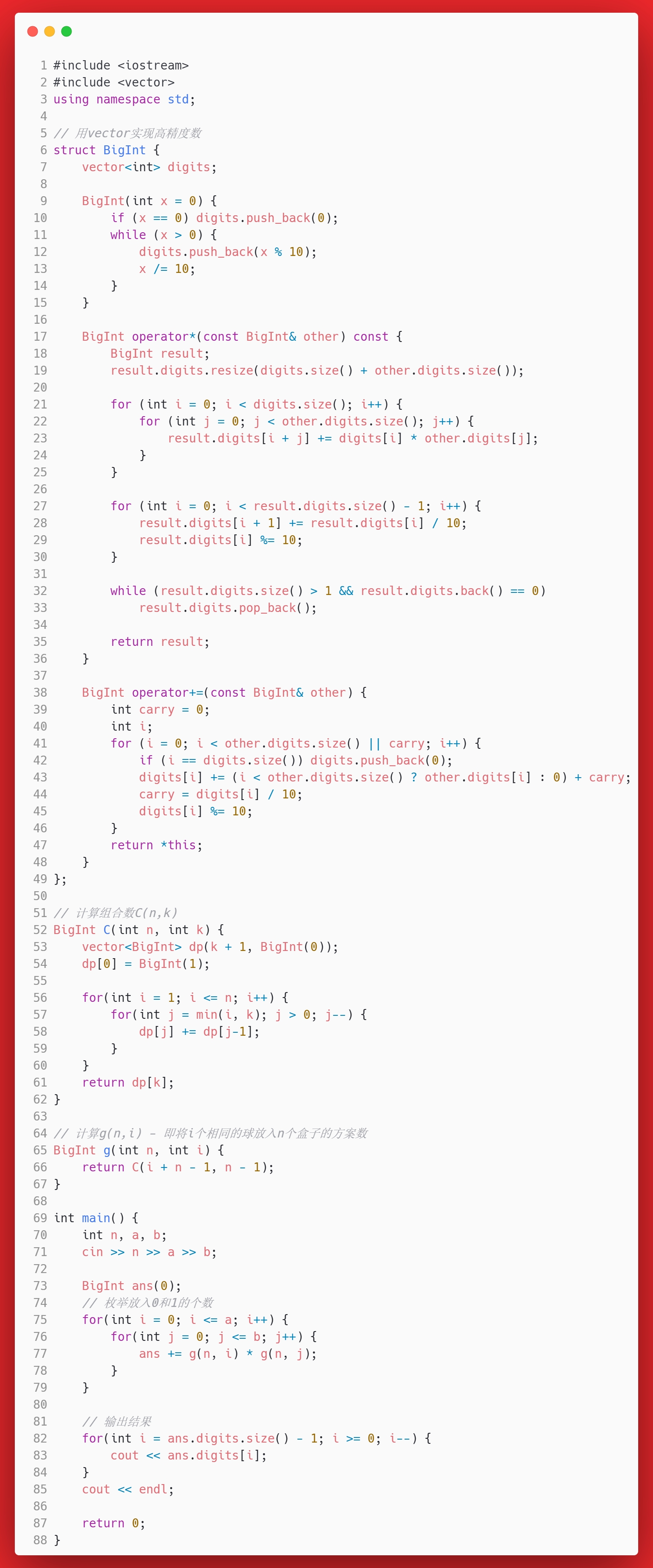
先剧透:这题需要用到高精度加法,否则最后的hack测试无法通过。
我们先暂时不考虑高精度的实现,而注重于算法。
我们假定,在n个盒子里放进去i个信号0以及j个信号1的计算公式是\(f(n, i, j)\)。显然,最终的答案是:\(ans=\sum_{i=0}^{a}\sum_{j=0}^{b}f(n, i, j)\)。
进一步分解,\(f(n, i, j)=g(n, i)\times g(n, j)\),也就是分别在n个盒子里放进去i个信号0的方案数乘上n个盒子里放进去j个信号1的方案数。
\(g(n, i)\)的算法
这是常见的所谓“隔板法”的应用:
先假定将k个球放进n个盒子,且每个盒子至少有一个球,那么,这k个球有k-1个间隔,我们要插入n-1个隔板(于是形成了n个独立“空间”),这样的组合数量是:\(C_{k-1}^{n-1}\)。
但现在出现有些盒子可以没有球,那么我们可以这么来:先在每个盒子里放一个球,然后按照上面的方法分配球,然后从每个盒子里拿走一个球就是了。此时球的数量变成了\(k+n\)个,但还是\(n\)个盒子,所以公式变为:\(C_{k+n-1}^{n-1}\)。
综合反推,公式变成:
\(ans=\sum_{i=0}^{a}\sum_{j=0}^{b}f(n, i, j)=\sum_{i=0}^{a}\sum_{j=0}^{b}g(n, i)\times g(n,j)=\sum_{i=0}^{a}\sum_{j=0}^{b}C_{i+n-1}^{n-1}\times C_{j+n-1}^{n-1}\)。
再结合高精度即可求解。
答案
思考
这道题还可以用DP来解。
这里我贴出核心代码:
dp[0][0][0].l = dp[0][0][0].a[1] = 1;
for(int i = 1;i <= n;i++)
for(int j = 0;j <= a;j++)
for(int k = 0;k <= b;k++)
for(int s1 = 0;s1 <= j;s1++)
for(int s2 = 0;s2 <= k;s2++)
dp[i][j][k] = dp[i][j][k] + dp[i - 1][s1][s2];
for(int i = 0;i <= a;i++) for(int j = 0;j <= b;j++) ans = ans + dp[n][i][j];这里DP的核心转换方程需要考虑第i个盒子放了s1个红球、s2个黑球的情形并转移。