洛谷：P2789：直线交点数

题目

P2789：直线交点数

分析

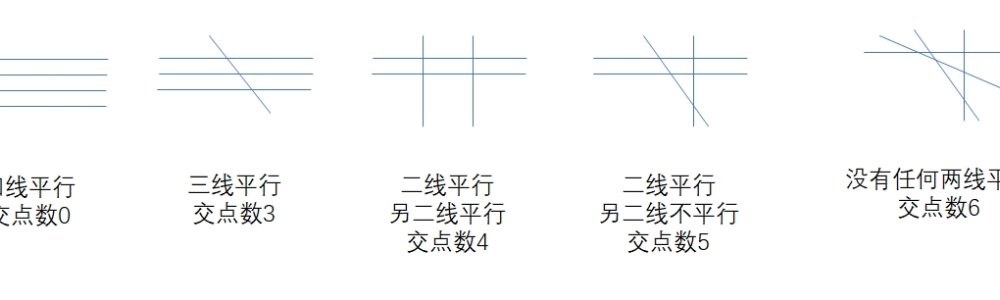
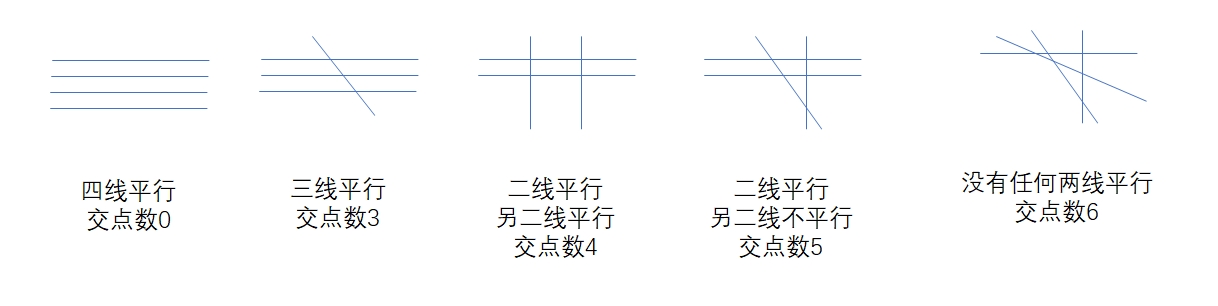
请注意，这道题不是求最多有几个交点（这个很简单：\(n(n-1)/2\)就是了），而是有几种不同的交点数量。

我们分析一下样本输入4而结果是5的情形。

当前状态	p (剩余直线)	m (当前交点)	循环 r (本组平行线数)	p-r (下次递归直线数)	r*(p-r) (本步新增交点)	下一调用	含义解释	抵达基准情形?	m 值, f[m] , ans
(4, 0)	4	0	4	0	0	(0, 0)	将所有4条线视为一个平行组。它们之间不产生交点。	-	-
(0, 0)	0	0	-	-	-	-	所有直线处理完毕。	是	m=0, ans=1
(4, 0) (继续)	4	0	3	1	3	(1, 3)	3条线平行，与剩下1条相交，产生3个交点。	-	-
(1, 3)	1	3	1	0	0	(0, 3)	处理剩下1条线。	-	-
(0, 3)	0	3	-	-	-	-	所有直线处理完毕。	是	m=3, ans=2
(4, 0) (继续)	4	0	2	2	4	(2, 4)	2条线平行(A组)，与剩下2条(B组)相交。	-	-
(2, 4)	2	4	2	0	0	(0, 4)	B组2条线平行。	-	-
(0, 4)	0	4	-	-	-	-	所有直线处理完毕。	是	m=4, ans=3
(2, 4) (继续)	2	4	1	1	1	(1, 5)	B组中1条与另1条相交。	-	-
(1, 5)	1	5	1	0	0	(0, 5)	处理最后1条线。	-	-
(0, 5)	0	5	-	-	-	-	所有直线处理完毕。	是	m=5, ans=4
(4, 0) (继续)	4	0	1	3	3	(3, 3)	1条线与剩下3条相交。	-	-
...	...	...	...	...	...	...	(中间过程略)	-	-
suv(0, 6)	0	6	-	-	-	-	所有线两两相交的情况	是	m=6, ans=5

最终ans的值为 5。

我们用类似递推/递归的方式，对4条线进行了分组：

1. 4条线为一组，剩下0条线，4*0=0，不产生交点（m=0）。所有直线处理完毕。
2. 3条线为一组，剩下1条线，3*1=3，增加了3个交点。所有直线处理完毕。
3. 2条线为一组，剩下2条线。
   1. 2条线为一组（也就是上面剩下的这2条线时平行的），剩下0条线，2*2=4，增加了4个交点。所有直线处理完毕。
   2. 上面剩下的2条线又分成两组，那么在3.1的基础上，增加了一个交点（因为这2条线不平行了），最终是5个交点。所有直线处理完毕。
4. …………

这个递归过程写成代码如下：

void suv(int p, int m)
{
    if (p == 0)
    {
        if (!f[m])
        {
            ans++;
        }
        f[m] = 1;
    }
    else
    {
        for (int r = p; r >= 1; r--)
        {
            suv(p - r, r * (p - r) + m);
        }
    }
}

答案

思考

为什么用递归而不是循环？

• 每次加入r条线会产生新的状态
• 需要遍历所有可能的r值
• 递归能自然处理这种组合问题