题目
分析
这道题目花了我很长、很长的时间!对AI的调教可谓一波三折!
当我看到能力值、可能重复(也就有了对应能力值的“频率”),然后在纸上做了几题后,发现有点像之前的那个“铺设道路”的题目。我能想到的类比,就是“将若干人员分成一组”类似于“找到一个连续的区间,放进石头,填高一米”的过程。如果非要说不同,那么“铺设道路”是填谷,我们现在是削峰。
另外,题目里出现了“最小分组的长度最大”这样的“最大最小”描述,可能会引发二分的思路,但不用这么麻烦。但是,这个提示还是告诉我们,在人数固定的情况下,分组越多,那么平均人数就越小。所以,一个合理的贪心策略,是尽可能多地拉人,少生成分组。
但这不意味着可以简单地从头跑到尾,因为每个数值的频率可能不同,所以前期太贪心的话,会造成某个数值的断层,而得不偿失:因为如此一来就会增加分组,而且这个分组的长度肯定比覆盖整个能力值的数字短。
必须说一句,网站里的样本数据没有代表性,因为它没有重复数据,也就不能洞察有了重复数据(因此各个能力值的频率不同)后的处理方式。
假定我们的输入数据是1 2 2 2 3 3。根据题目要求,合理的分组应该是:[1 2] + [2 3] + [2 3]。6人分为三组,每组最少也有两人。其他分法会出现一个人一组的情形,不符合题意。
看下图示,我们会找到算法的思路,并知道我们上文提到的类比是恰当的:
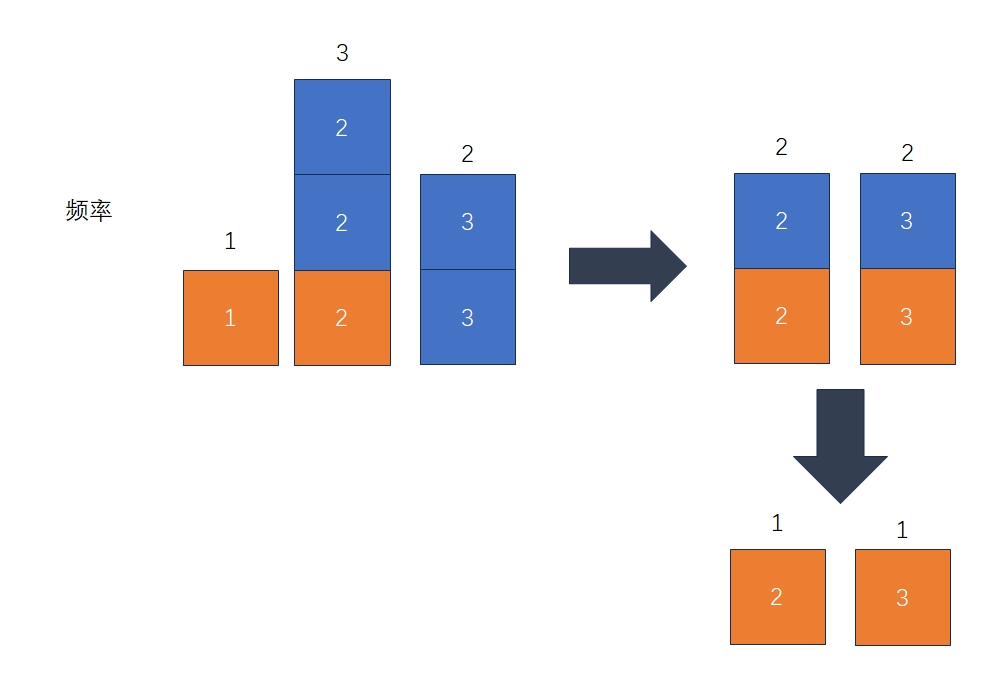
我们注意到,这里的能力值是必须排好序的,但其对应的频率值可能会出现“逆序对”。
如果用“逆序对”来判定拉人标准的话,就是不断向右拉人,直到出现一个逆序对为止。图中的第一步,就是从(频率)1到3(对应了能力值1和2),但不能到频率2,因为3>2,构成逆序对。
这么做的出发点(不是严格证明)在于:如果右边数字(也是较大的数字)的频率比较小,那不能太早拉进来——原因我们上面已经分析过了——我们要让他多为后续拉人做贡献。
所以核心算法就是(伪代码):
当然,过程中,要不断将频率降低,因为随着某个能力值的人被拉入,这个能力值出现次数就少了。
最后,频率如果已经变成了0,应该将这个数字拿走,不然我们每次拉人的时候,还要处理0这个特殊值——不处理的话,可能导致频率为负而死循环了。
答案

思考
这道题目还有一个“可恶”的点,上述代码,如果用标准的C++代码写,会造成最后一个测试用例超时。实在没办法了,只好将所有的输入、输出代码改成C中的用法——然后就通过了所有的测试。
这实在不应该是一个认真的题目应有的做法!