洛谷：P5076：普通二叉树（简化版）

题目

P5076：普通二叉树（简化版）

分析

这道题主要是考核二叉树中二叉搜索树的一些基本操作：插入、查询x的排名、查询排名k的元素、查询x的前驱和后继。

插入

二叉搜索树的插入必须保证一点：以某个根节点为边界，左子树所有节点的“值”小于根，右子树所有节点的“值”大于根。如果有相同的值，那么只增加计数。因此，节点的结构需要定义为：

struct Node
{
    int left;   // 左子节点索引
    int right;  // 右子节点索引
    int size;   // 子树大小
    int value;  // 节点值
    int count;  // 当前值的数量

    Node() : left(0), right(0), size(0), value(0), count(0) {}
    Node(int v) : left(0), right(0), size(1), value(v), count(1) {}
};

left/right/value是基本的、也是必须的。count用来保存本节点value出现了几次。而size是个“辅助”性的成员，保存了子树的大小。这样一来，可以方便地进行查询排名的任务。

插入有两个步骤：

1. 插入元素：当然需要判定插入到左边还是到右边——这是递归实现的。
2. 更新大小（size）：无论元素插入在哪里，都会影响对应诸多根节点的size：它应该等于左树的size+右树的size+本身的count。

// 更新节点的子树大小
void updateSize(int node)
{
    if (node == 0)
        return;
    tree[node].size = tree[tree[node].left].size + tree[tree[node].right].size + tree[node].count;
}

// 插入一个数
void insert(int &node, int value)
{
    if (node == 0)
    {
        node = ++nodeCount;
        tree[node] = Node(value);
        return;
    }

    if (value == tree[node].value)
    {
        tree[node].count++;
    }
    else if (value < tree[node].value)
    {
        insert(tree[node].left, value);
    }
    else
    {
        insert(tree[node].right, value);
    }

    updateSize(node);
}

查询x的排名

• 从根节点开始查询。
  • 如果\(x\le node.value\)，那么x在左树，只要返回它在左树的排名即可。
  • 反之，那么x在右树，需要返回左树的size+右树的排名+节点的count。
• 特别约定：根节点的排名是1。

代码略。

查询排名为k的值

• 同样判定在左还是在右，先得到左树的大小（leftSize）。
  • 如果\(k\le leftSize\)，那么必然在左树，继续递归找。
  • 如果\(k\le leftSize+node.count\)，表明它一定在节点上，返回节点的值（value）即可。
  • 否则，一定在右树，且它在右树的排名是\(k-leftSize-node.count\)。
• 特别约定，如果找不到，则返回-1。

代码略。

查询x的前驱（小于x且最大的数）

还是根据二叉搜索树的特性，分左右。

• 如果\(x\le node.value\)，表明在左树，递归找左树。
• 否则要在右树找。
• 特别约定，如果x是根节点，那么返回一个INT_MIN。

代码略。

查询x的后继（大于x且最小的数）

基本思路和找前驱类似，不赘述。

答案

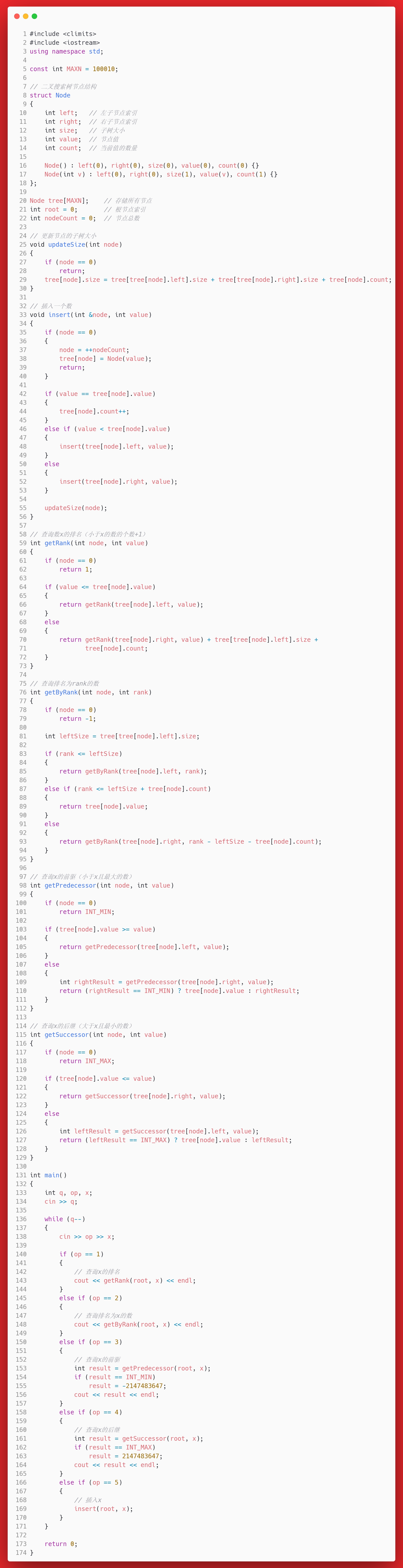
思考

想清楚二叉搜索树的结构后，这道题目也就很简单了。