题目
分析
AI提示我们,这是一道“谢尔宾斯基地毯问题”。
这道题不难。根据题意,直觉告诉我们,可以分而治之:每个区域(除了左上角区域),都可以再分四个区域;这四个新的小区域,除了左上角的其他三个区域,还可以继续分割……由于这个区间的长宽都是\(2^n\),可以保证不断均匀分割——直到边长为1为止——看!分割的终止条件也出来了!。
接下来就是分析一个正方形的设定。一般而言,在编程中,正方形由三个参数确定。本题中可以用左上角的坐标(x, y)以及边长size来决定。知道原始正方形的坐标后,新的四个区域正方形的坐标可以确定如下:
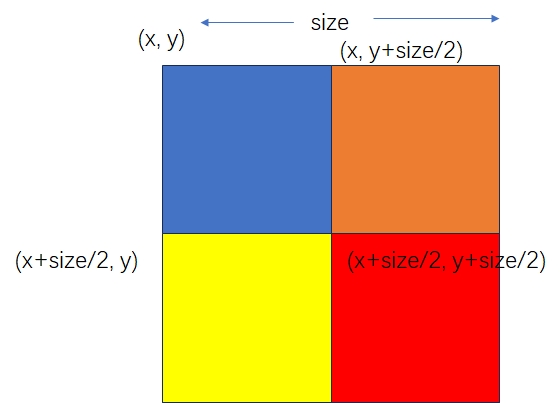
注意,这里的x和y坐标轴和方向和我们常用的不同。X轴是从上到下(和数组的行数对应),Y轴是从左到右(和数组的列数对应)。
基本的处理流程就是:
在我们的坐标设定中,因为我们是从左上角开始(\((x=0, y=0)\)),切分为四个方块后,左上不用操作,而右上、左下、右下三个方块的起点坐标可以很快得到:
- 右上:\((x, y+\frac{size}{2})\)
- 左下:\((x+\frac{size}{2}, y)\)
- 右下:\((x+\frac{size}{2}, y+\frac{size}{2})\)
同时,根据这个核心处理流程,我们一开始就应该将所有位置设置为0(全都赦免)。我们通过将数组设置为全局变量即可。
答案

思考
这是一道很好的理解递归和分治的入门题目。
洛谷配套书《深入浅出程序设计竞赛(基础篇)》在讲到本题时,用了一个稍微不同的解法,其solve函数的声明是:
void solve(int x, int y, int n)
{
if(n == 0) a[x][y]=1;
else {
solve(x + (1 << n - 1), y, n - 1); //左下
solve(x, y + (1 << n - 1), n - 1); //右上
solve(x + (1 << n - 1), y + (1 << n - 1), n - 1); //右下
}
}
它这里在传递第三个参数的时候,不是直接用分割后的小方块的大小,而是传递了新的n,如果之前的一个大格子的大小是\(2^n\),那么分割一次后,四个小格子的长宽都是原来的\(\frac{1}{2}\),也就是说\(2^{n-1}\)。也因此,递归终止条件是n==0了。这些细微的差别需要注意,因为这会直接影响初始调用以及其他代码,但都不是很大的变化。
另外也请注意,洛谷的代码是x + (1 << n - 1),更不容易混淆的写法是:x + (1 << (n - 1))。如果对运算符优先级没有把握,建议用括号来帮助自己明确。
