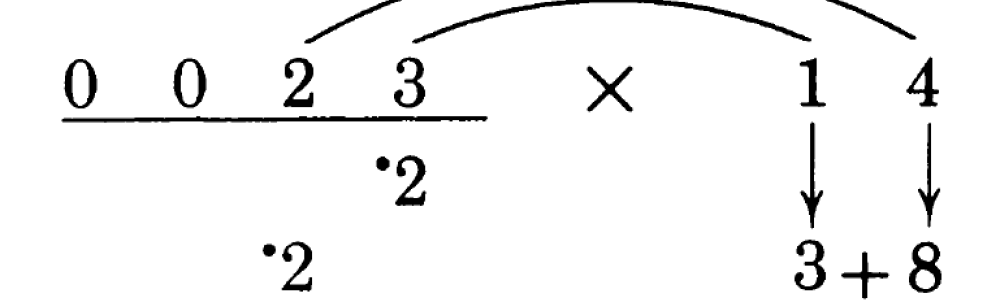本页面已浏览198次

用直接法进行快速乘法

在本章中我们学习如何进行任意位数乘以任意位数，而且是直接得到答案而不需任何中间步骤。比方说我们要计算625*346，那么计算步骤就会是这样：

\(\frac{000625}{216250} \times 346\)

不用额外写下任何东西。我们只会写下问题，然后立即写出答案。

有两种方法做到这点，它们各自在特定场合有各自的长处，但是总归能得到正确的答案。幸运的是，两者有有多地方类似，所以学起来也很容易。本章中我们要学习所谓的“直接”法：如果被乘数中包含小数字（如1,2,3等），这个方法就很合适。然后在下一章，我们会用一种所谓的“快速乘法”，它包含直接法，同时又有一个新的特性。这一新特性帮助我们处理包含大数字（比如987*688）时碰到的困难。

解决任何问题时，都可以使用随便哪种方法，而且都能得到正确答案。我们刚才提到了偏好的一个理由，但只是为了方便。在特定场合你应该根据自己的判断要做出选择。

顺便提一下，类似直接法这样的方式在本系统引入之前可能就已经由数学速算人员使用过。这些“数学奇才”以其惊人的心算能力让观众啧啧称奇，对他们用的技术一直保持神秘，但是看起来他们应该必定用到了与我们的直接法类似的方法——可能做了一些变更。

短乘法：两位数乘以两位数

假定我们要计算23乘以14。我们写成这样：

\(\frac {0023}{????} \times 14\)

乘以一个两位数时，我们总会在被乘数前加两个前导0。

第一步：被乘数最右一位（23中的3）乘以乘数最右一位（14中的4）。答案中写下2并记下进位1：

\(\frac {002\dot{3}}{???\dot{2}} \times 1\dot{4}\)

第二步：我们要获得23中2这个数字下的答案，需要找到两个数字（两个部分乘积）然后将其相加。第一个是8，来自2*4：

\(\frac {00\dot{2}3}{???\dot{2}} \times 1\dot{4}\)

第二个部分乘积来自另外两个数字的乘积（3*1）：

\(\frac {002\dot{3}}{???\dot{2}} \times \dot{1}4\)

然后我们将这两个部分乘积相加：8+3=11。这个是我们要的结果，不过还要加上进位1，所以得到12，我们写下2并进位1：

\(\frac {0023}{??\dot{2}\dot{2}} \times 14\)

最后一步：被乘数和乘数最左边的一位相乘（2*1）：

\(\frac {00\dot{2}3}{?3\dot{2}\dot{2}} \times \dot{1}4\)

本例中我们不需要用我们写在前面的最组边的那一位0。它只是为一旦出现进位预留一个数位空间。

第二步是新的一步。我们用两个数字来得到答案中的一个数字。我们将部分乘积8加上部分乘积3，得到答案中要用到的11。8和3来自两组数字的乘积，我们称其为“外对”和“内对”。

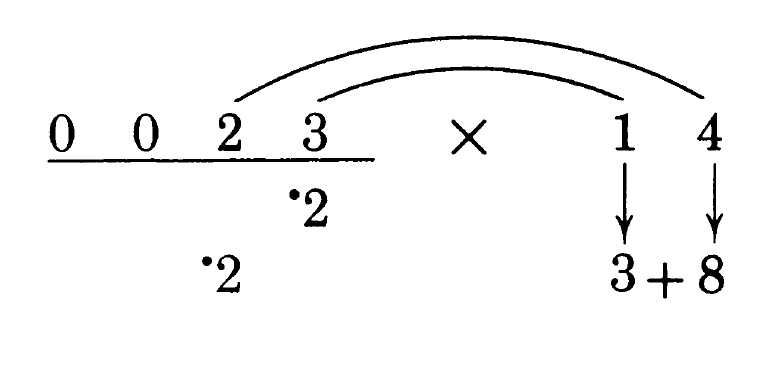
找到这些配对的规则如下：被乘数中我们目前要操作的那一位（也就是在答案中要找的那一位数的上边一位）就是“外对”之一，上例中就是23中的2。“外对”中另外一个数字是乘数的最右边一位，因为那是在外的一个数字（上例14中的4）。而另一对（“内对”）是刚指定的外对两个数字各自往“里面”找的那一个数字，在上例中就是23中的3和14中的1。

“外对”和“内对”会被经常使用，所以我们要搞清楚。下面举三个例子：

我们来计算38*14：

\(\frac {0038}{????} \times 14\)

第一步：首先我们要做的就是进行8乘以4，得到32。写下2并进位3。¹

\(\frac {003\dot{8}}{???\tilde{2}} \times 1\dot{4}\)

第二步：要找到下一个数字，我们需要使用外对和内对。38这个数字中我们现在开始处理3，这是因为3正在答案的下一个数字所在位置的上方。所以3是外对之一。外对的另一个数字是？应该是14中的一个数字，对，就是4，因为它是14这个数字中“外部”的那个数字。内对就是这两个数字里面的那两个（也就是8和1）。

现在计算：\(3\times 4=12，8 \times 1=8\)。这两个值加起来得到20，还要加上进位3，所以得到23。写下3并进位2：

\(\frac {0038}{??\ddot{3}\tilde{2}} \times 14\)

最后一步：将两个最左边的数字相乘，得到3，加上进位2就是5：

\(\frac {00\dot{3}8}{?5\ddot{3}\tilde{2}} \times \dot{1}4\)

下面有两个例子，但是以简约形式写出。划线下的是进位数字。看看你是不是能自己找出这些“中间”数字是从哪里又是怎样得来的：

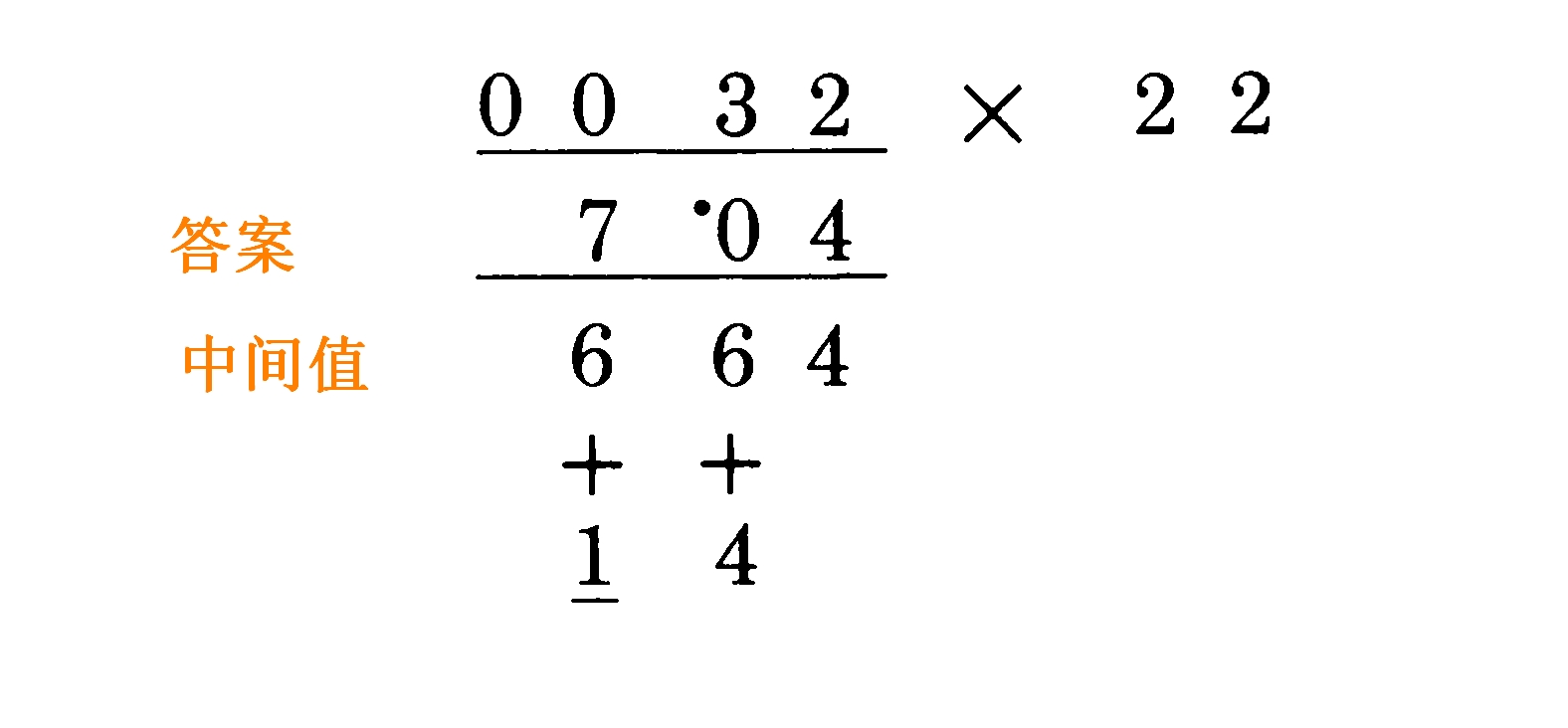
为了让你有信心已经掌握了这个方法，我们请你做一些习题：

• 0031 * 15
• 0017 * 24
• 0073 * 64
• 0034 * 21
• 0042 * 26
• 0048 * 52

（答案略）

如果回忆一下刚才的过程，你会发现这是很自然的过程。你一直是在将两个两位数进行相乘。为了做到这点，你将两个最右的数字相乘，得到答案最右的一位数字，比如在23*14时，你进行了3X4的运算。将两个最左的数字相乘，得到答案最左的一位数字，比如在23*14时，你进行了2X1的计算。为了得到答案的中间数字，你用到了内对和外对。每一对都有两个数字乘在一起，于是每一对都给出了一个数字，然后这两个数字加在一起得到中间的那位数字。

接下来我们还会用到内对和外对。事实上，我们要大量使用。当然，在你自己解决问题的时候，你不用画出连线标注出一对数字。前面我们这么做只是为了解释一下我们要做什么。实际运算中，可以这么来确定外对，因为事实上它包含的那个被乘数的位数正在下一个空位（也就是答案下一位出现的位置）的正上方。内对的数字就在外对的数字之内。

长被乘数

如果被乘数很长，我们要做的无非是重复第二步，直到被乘数各位都用完。比方说，我们要进行312*14。这只是三位数乘以两位数，但是很能说明我们要讲的点：

第一步：将312最右一位和14最右一位相乘：

\(\frac {0031\dot{2}}{????8} \times 1\dot{4}\)

第二步：现在开始使用外对和内对。下一个我们要处理的数字是312中的1，也就是答案中下一个数字的位置的正上方的那个数字，所以312中的1就是外对的一部分：

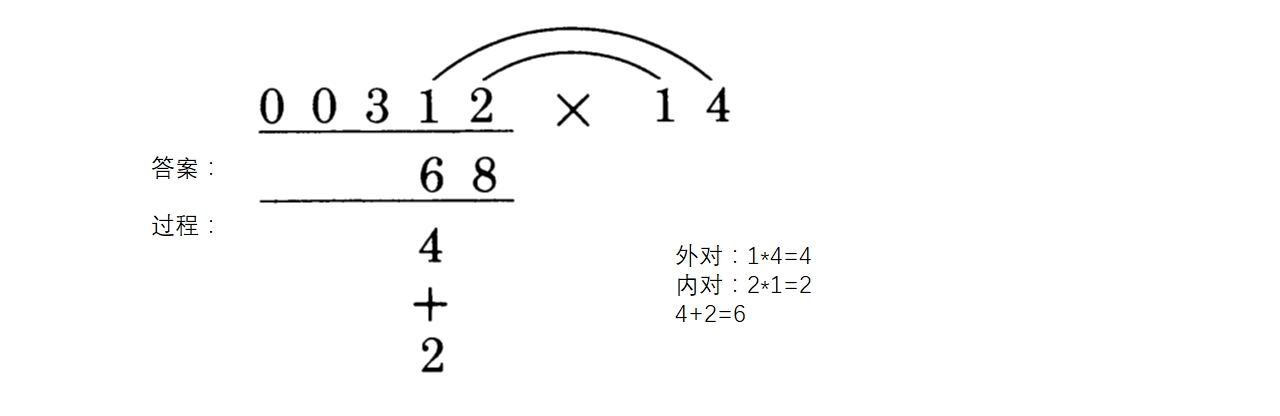
第三步：这就是再做一次第二步，但是我们要移动这些对的箭头。也就是说，我们会有不同数字得到的对。但是，312中我们要用到的下一个数字，也就是答案下一位正上方的那个数字，是外对的一部分。这点还是如此。本例中，3是我们新的外对的一部分。于是：

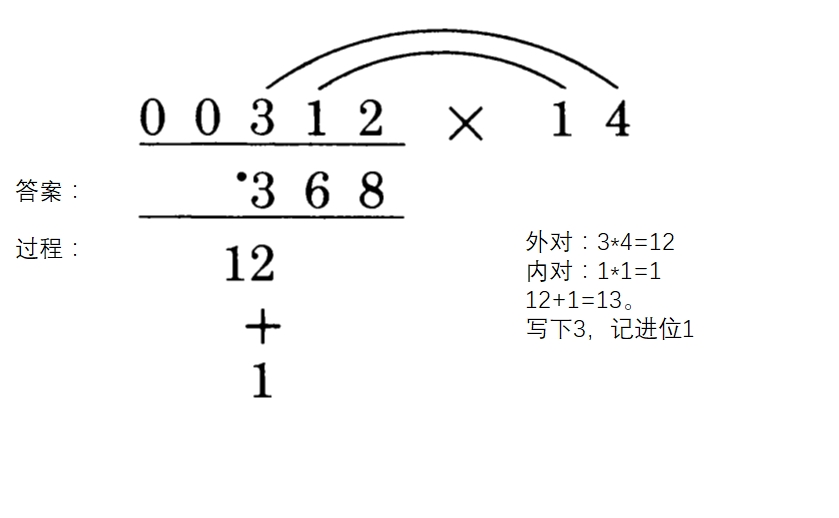
最后一步：要找到答案的最左边一位，将两个最左边的数字相乘，3*1加上进位1：

以后，我们需要将连线连到被乘数的前导0上。为了让大家知道是怎么回事，我们这里做个示范。记住：任何数字乘以0都等于0。

在乘法中，零消灭了所有其他的数字。100万乘以0还是等于0。利用这个事实，我们做最后一步的时候，就像它是一个中间步骤一样：

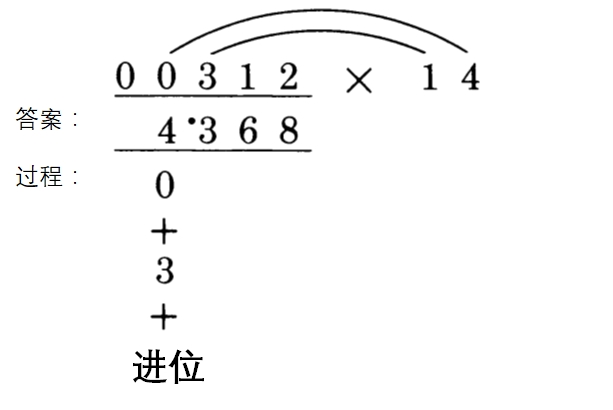
外对中\(0\times 4=0\)，内对中\(3\times 1=3\)。0+3=3，加上进位得到4，这和我们之前的答案是一样的——必须如此啊，因为刚才我们得到的是正确答案。这表明我们可以用第二步和第三步一样的方法来完成最后一步。也就是说，我们应该通过外对和内对，而不是用一个特殊的规则来进行最后一步。

每次我们连线一组数字并将其标记为“计算”，我们需要知道的是在实际工作中，这些都是在大脑中完成的。如上文的这些展示只是为了进行说明而已。你在进行处理时，应该只写下你要相乘的两个数以及答案。

我们刚才展示的例子再次表明外对是如何获得的。它总是由这个事实确定：它包含的被乘数中的数字在需要计算的下一位答案的正上方：

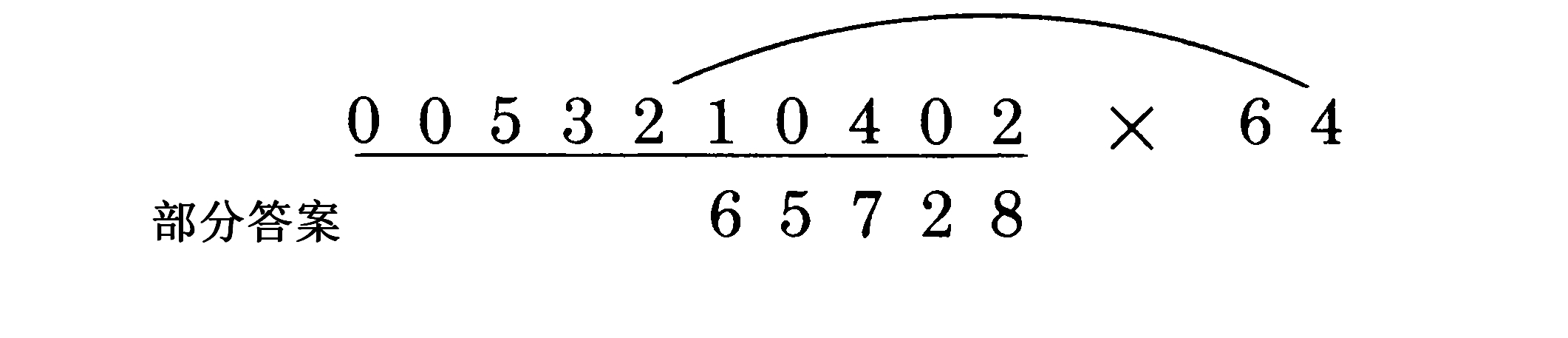
连线的另一端必须连到该二位数乘数的右边那位数字，因为那是外对的一部分。而内对就由这两个数字靠里的那两个数字构成。

实际应用中，你可能会发现用手指盖住数字来标记外对和内对数字的位置会是个不错的想法。这么做没有额外的麻烦，但是防止了在思想中忘记位置而产生的错误。在312*14这样的三位数乘以两位数计算中，失位的危险不是很大，但我们很快要计算更长的数字。不论如何，值得注意的是要清楚地写下数字并适当分开，并在答案所属的那个数字之下写下答数。整洁能帮我们避免不必要的错误。这不光适用于我们现在的工作，而且对常规的乘法、任何类型的除法以及加减法都有用。整洁是一个需要培养的好习惯。

有个方法来检查你对这个方法的了解有多么深。下面是311*23的完整例子。答案在311之下，以及一系列的中间步骤（应该在脑海中完成）列在了答案下面。现在用一张纸盖住答案和中间步骤，在大脑中计算答案的最右一位。把纸张移开一点，足以让你看到答案，你就知道你是不是做对了。然后计算下一位，得到下一位后，移开纸张看答案的下一位，确定你是否做对。如果没做对，将纸张移动而显示该数字的中间步骤，看看这个数字是怎么得到的。在每个答案的中间步骤中，这些数字是要加起来而得到答案：

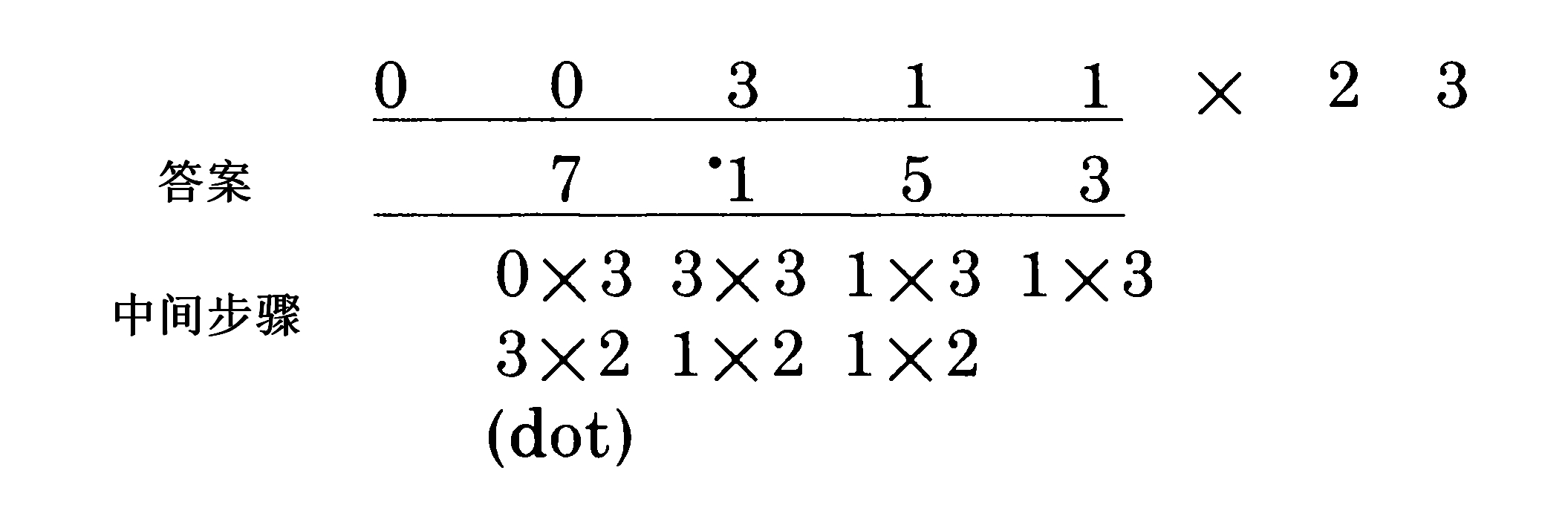
前导0

到目前为止我们看到的例子中，在被乘数之前都有两个前导0，但实际上一个0就够了。不过有时候我们需要两个前导0。考虑这个例子：

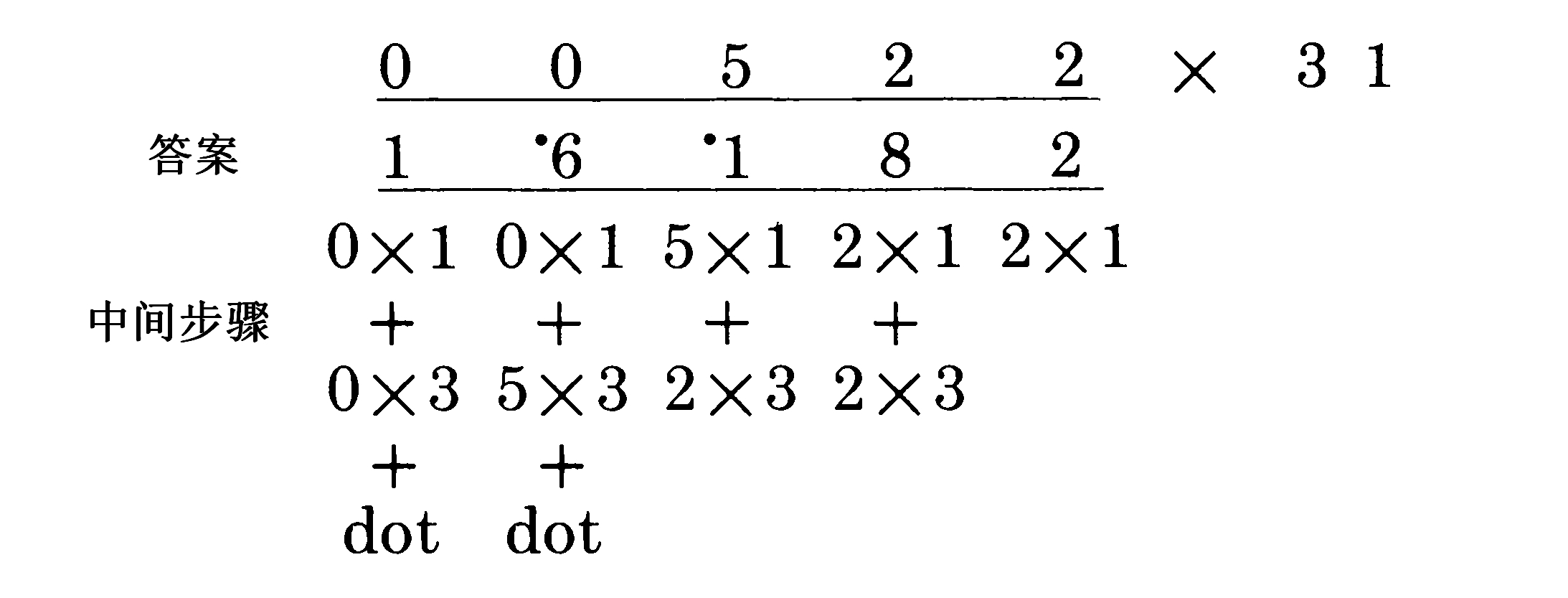
这时，我们在第二个0下面有了个数字，也就是最左边的那一位。需要注意的是，这个数字就是进位的1。31并没有给出任何数字，因为它们都和0相乘，所以只有进位保留了下来。

这也解释了为什么在我们之前的运算中不需要两个前导0。被乘数前有一个0就够了，因为在最后一步不需要进位。

一般规则：乘以任意长度的乘数时，在被乘数前加上和乘数位数一样多的前导0。

我们看到，有时我们不用那么多0，但是遵守这个规则没有任何坏处。如果实际只要一个0但是我们还是用了两个0，我们只会发现在最后一步我们不用写任何东西。

到目前位置我们只考虑了两位数或者三位数的被乘数，但是更长的数字（比如241304）也是一样的处理方法。我们只要不断重复乘以两对数字加上结果。假定你要计算241304*32：

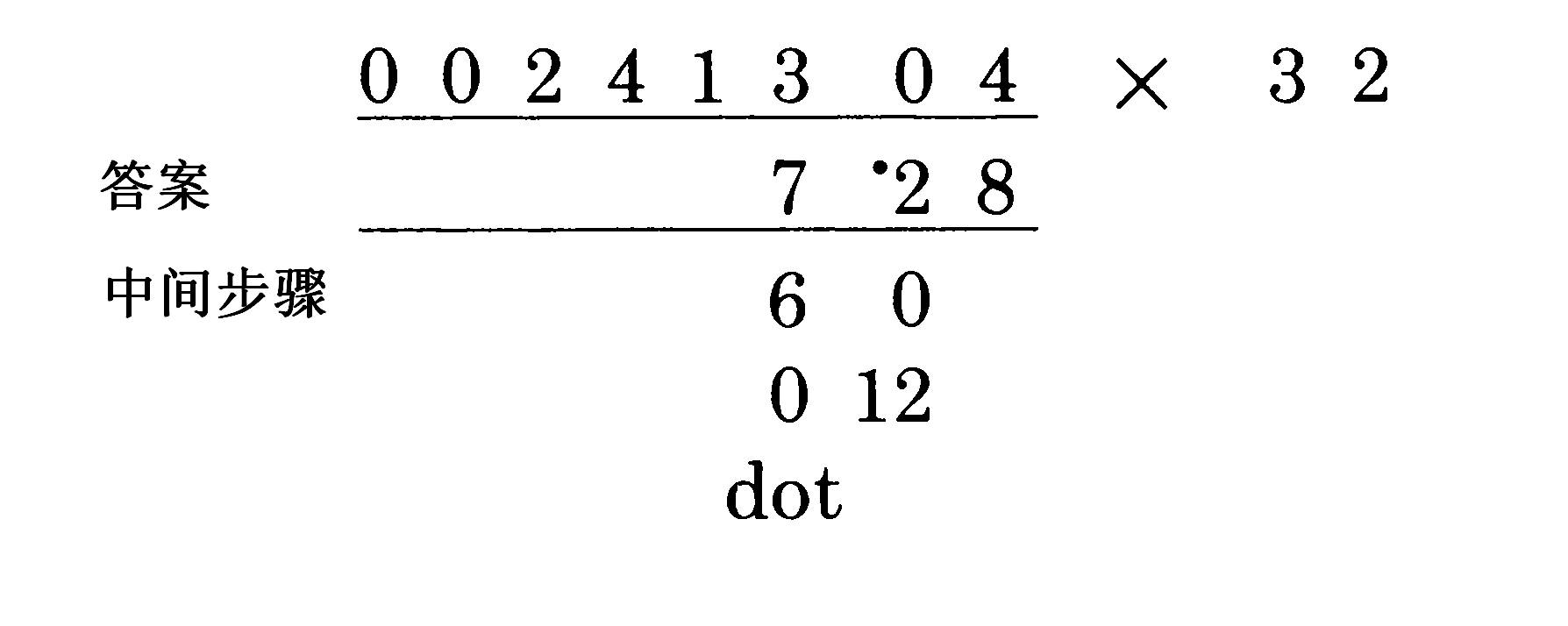
到此，就是我们之前所做的三位数乘以两位数。下一步也是同样的做法：

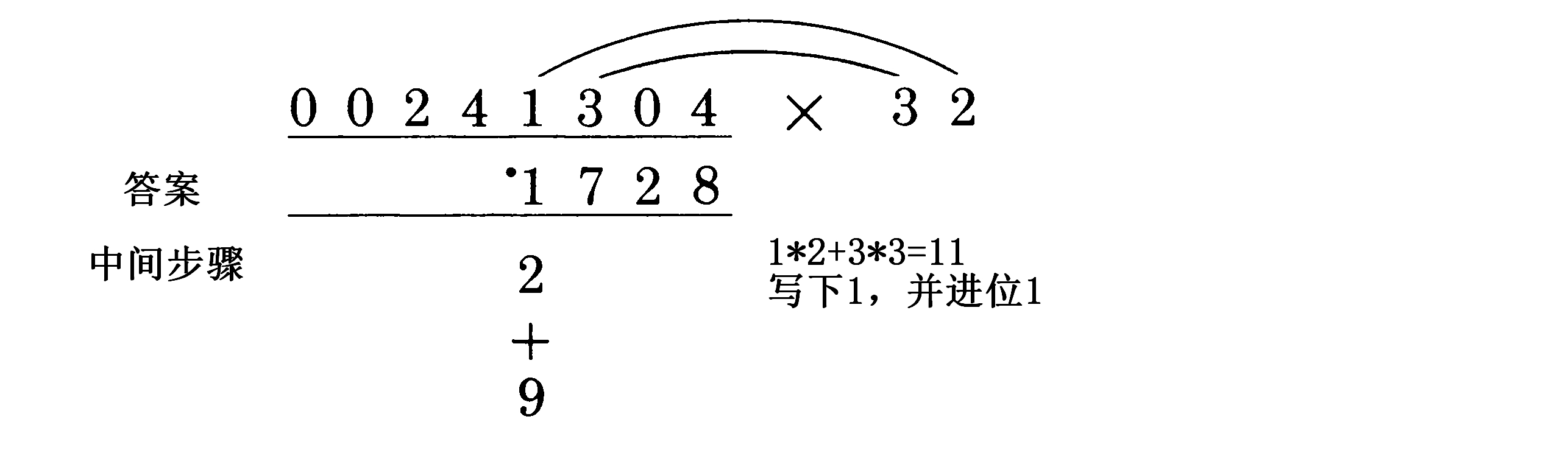
显然，我们加上2和9，得到11作为答案的下一个数字。我们写下1作为答案的一部分并记下进位1。我们继续往左移动。下一对是4/1和3/2，于是得到42+13。完整的答案如下：

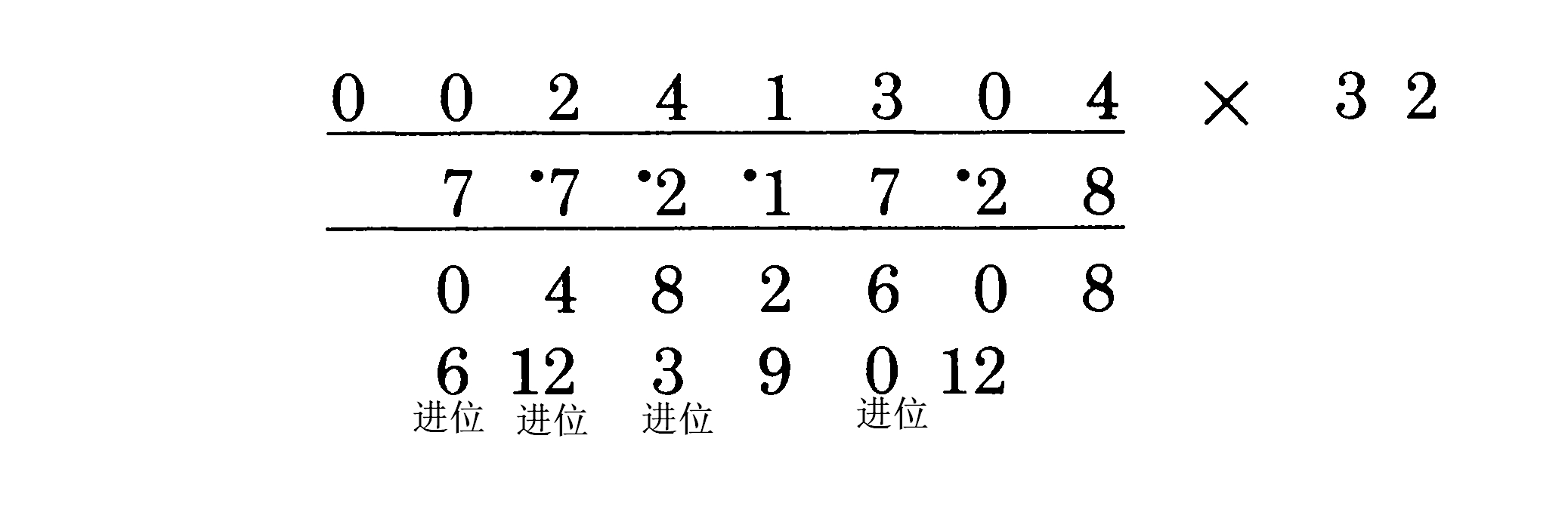
最左边的零并没有用到。这是在最后一步计算中没有进位的情形，因此在最后一个零下面不用写什么东西。我们写下这个零只是为了完整性的要求。规则要求在乘数有两个零的时候补两个前导零。有一个零被浪费了，但说来说去，一个零又能造成多大的代价呢？一点也没有！

我们来做个小小的“思想实验”：你不用进行任何直接的计算就可以得到答案。从上面的例子中你应该知道，311*23=7153，那么31100*23等于多少？唯一的不同是被乘数的结尾多了两个零。答案是多少？在阅读下节之前，先确定答案。

你毫不迟疑地对自己说，答案是715300。被乘数结尾多出来的两个0来到了答案中。这点总是如此。被乘数尾部不管放了多少个零，也不管这个被乘数是怎样的，这些零都要被直接带到答案中，并放在答案的尾部。

有四种可能的方法来做到这点，你用的是哪一种？也许你足够聪明，可以同时用到好几种方法。那么我们来看看这四种方式：

• 猜的。这个单词不好听，所以我们用一个更好听的同义词。非数学家通常称其为“常识”，数学家称其为“数学直觉”。不管名字如何，这个方法常常犯错，但也常常够用。
• 记忆。你想起你还在读书那会这些事情是怎么搞定的。如果记忆已经开始不清，那么可以称为一半记忆一半“常识”。
• 乘以零。我们知道零乘以任何数字都还是零。显然，如果我们将23乘以31100尾部的这两个零，我们还是会得到零——直到我们来到了31100中右边那个1的时候。两个零相加还是零。直到我们开始处理31100中的311部分之前，我们都只能得到0，然后就和311*23的结果一样了。
• 交换律。这是一个数学家会采用的方法。基本的想法是，我们进行两个以上的数字相乘时，这些数字如何分组是无所谓的，只要我们最终在做乘法时把这些数字都用上就对了。比方说，2*3*4。直接了当的做法是，23=6，64=24，答案是24。但是如果我们愿意，我们可以先做34，234=212，答案还是24。此外，我们还是重排：234和243或者8*3都是一样的。答案都是24。

现在将交换律应用到31100*23上。我们将其看做是311*100*23。进行交换：这等同于31123100。于是我们先进行311*23——这个是我们之前做过的题目，我们已经知道答案是7153。然后我们将其乘以100。一个数字乘以100只要在后面加两个零就可以了。因此我们在7153后面放两个0，得到715300，和之前一样。

第四个方法的好处是，它告诉我们在其他特定的情形中该如何处理。假定多出两个零在23的尾部。我们要计算311*2300，通过第四种方法的推理，我们知道这两个零必须出现在答案的尾部。我们还是得到715300。事实上，如果一个零在311后面而另一个在23后面，我们要计算3110*230，这两个零都还是出现在答案尾部，还是得到715300。

规则：将被乘数和乘数尾部的所有的零收集起来，放到答案的尾部。然后开始乘法运算而不用管这些零。

比方说，这是我们的第一个例子：

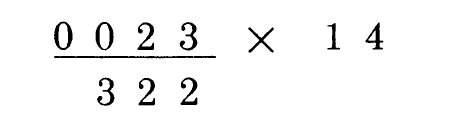
假定我们要计算230000*140，答案是多少呢？只要做上面这个简单的乘法，不要考虑零，然后将这总共5个尾部的0归并写道答案的尾部：

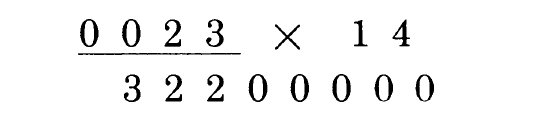
答案就是32200000。

三位数的乘数

到目前为止，我们一直在进行的乘法都是各种数字与两位数的乘数相乘。被乘数可以很长（比如241304），但乘数只有两位（比如32）。我们应该如何进行乘数为三位数的乘法？

我们先看一个例子：213*121。乘数有三位，于是我们在被乘数前补写三个零：

\(000213 \times 121\)

这个和我们之前提到的规则是吻合的，也就是要在被乘数的左边加上乘数位数那么多的0（我们知道，有时有些零会是多余的）。接下来我们分步来看过程，每一步找到答案中的一个数字。

第一步：\(\frac {000213}{000003} \times 121\)，3*1=3

第二步：

到目前为止，在前两步中，我们所做的不过是之前做过的东西。我们现在进行的计算就好像是在进行13*21，而不是213*121那样。

第三步：这一步是新的：为了获得下一个数字，我们要加上三组数字的乘积，而不是两组：

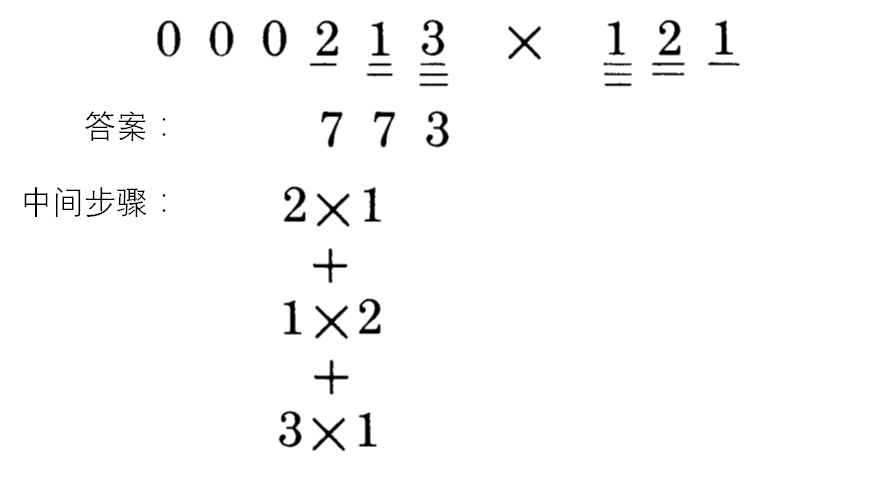
这个“步骤”怎么做，可以观察数字是如果得到的。为了更清楚地看到这点，我们可以和之前一样在“外对”和“内对”数字上画连线，但是此刻我们要加一个“中间对”：

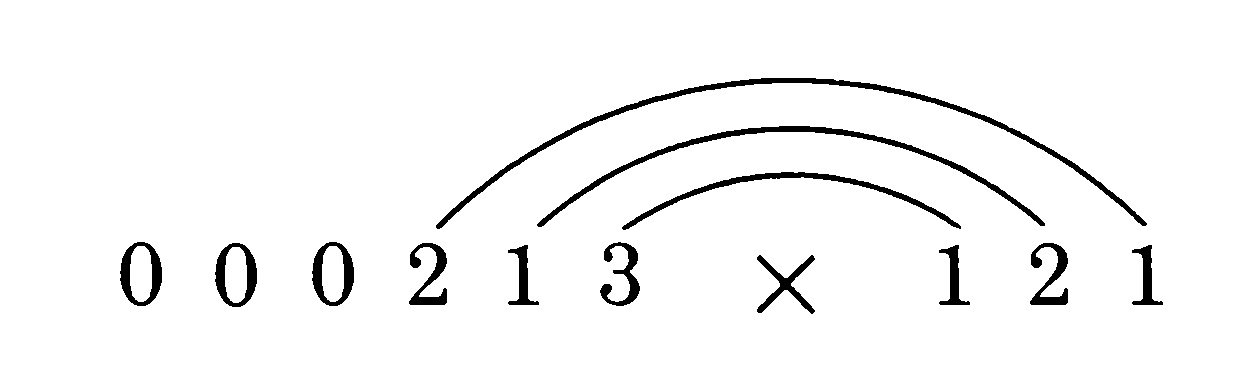
外对连接了213中的2和121中最右边的1。所以外对是21=2，这将答案的一部分。然后我们往里看。“中间对”连接了213中的1和121中的2，于是得到12=2。这是答案中的第二部分。第三部分也是最后一部分来自内对，3*1=3。将这三部分加起来：2+2+3=7，也就是答案的下一个数字。外对的2和1用和以前一样的方式确定：答案的下一位数字之上的被乘数中那位数字构成了外对的一部分。外对的另外一个数字来自121最右的一位。与这两个数字相邻的两个数字构成中间对，而最后的两个数字当然就构成内对。

剩下的工作就是用三根连线将这个步骤加以重复，但要不断地将连线往左移动。

第四步：

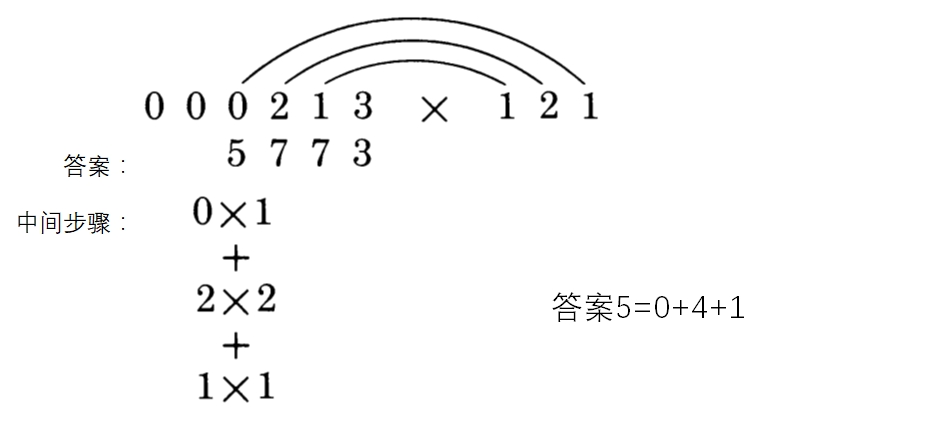
最后一步：

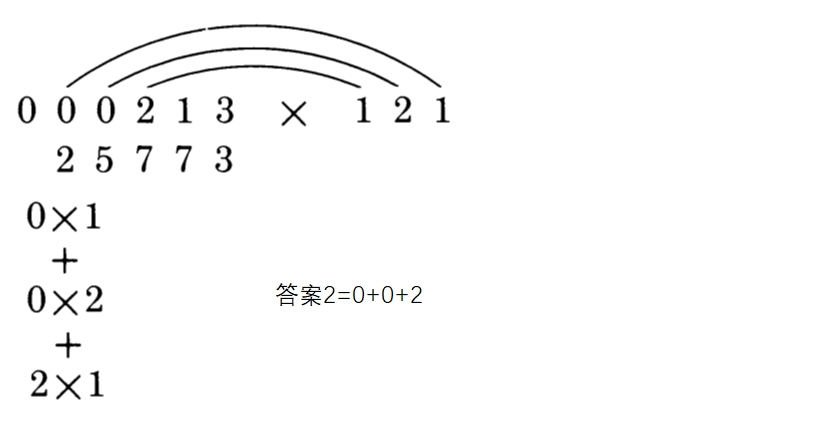
在本例中，这是最后一步，因为我们得到数字2而且没有进位。答案前有一个0，只是因为考虑到最后一步中可能有进位。既然现在没有进位，那么我们也就结束工作了。答案就是25773。

当然了，这个例子看上去很长，这只是因为有很详细的说明。在实际操作中，计算要迅速得多。下面这个例子是更接近实际运算的形式。在数字下划线取代了用手指指定数字然后“向里移动”来标记外对、内对的做法。单划线的两个数字要相乘，双划线的两个数字相乘，三划线的两个数字相乘：

第一步：

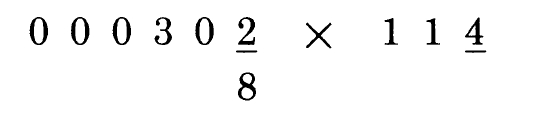
第二步：（当然了，在实际计算中，我们不会再写中间步骤的数字了！）

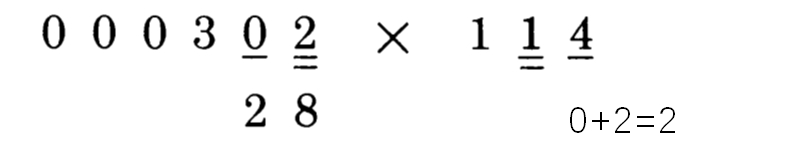
第三步：

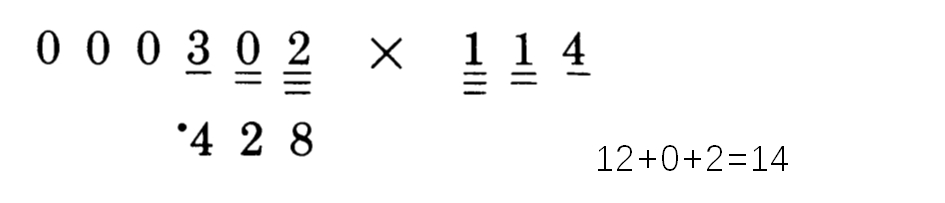
第四步：

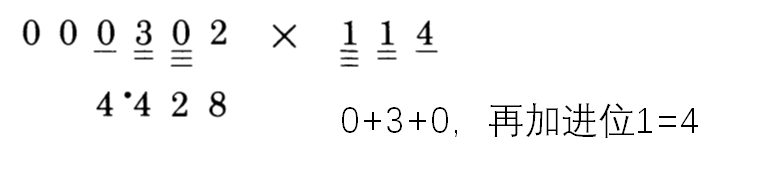
最后一步：

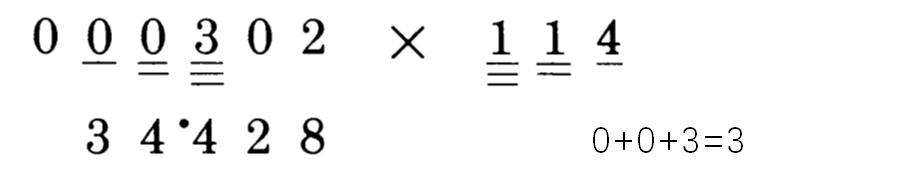
这就是最后一步，因为没有进位。如果有进位，我们需要在最左边的0下面写上1。如果有进位2，那么我们就写下2。但在本例来说，计算已经结束，答案是34428。

记住，0乘以任何数字都是0。

最后，我们自己做一个题目，看看实际操作中有多么简单：

\(000203 \times 221\)

一开始，是203中的3乘以221中的1——你肯定毫无疑问地这么做了。然后你用内对外对的形式将0 3乘以2 1，并将结果相加；以此类推。答案自然就是你得到的44863了。

如果你愿意的话，在实践中你可以创造新的例子然后开始运算。从两位数乘以两位数开始应该会简单一些，比如23*31，然后再到三位数。

这个方法可以应用在任意长度的被乘数。但是，如果有一个数字很长而且包含很大的数字（比如9869），我们就会发现使用本章的方法时，要“进位”很大的数字。这也是在我们的例子中我们偏好用比较小的数字（比如2或者3）。如果你试了一两个有很大数位的例子，你会对下一章我们要看的“快速乘法”感激不尽，因为它只要求我么进位1或者2。与此同时，本章的方法在数位比较小的时候会非常方便，而且它也是下一章不可或缺的一部分。

乘以任意长度的数字

如果乘数位数更长，我们也会使用同样的原则。四位数乘数（比如3214）是这样来进行操作的：答案的每一位数字都是通过四部分加起来的。这四部分数字的每个数字都是两个数字相乘的结果。是哪两个数字呢？：连线两端的两个数字；换句话说，就是内对和外对。我们举个例子看下\(2103\times3214\)：

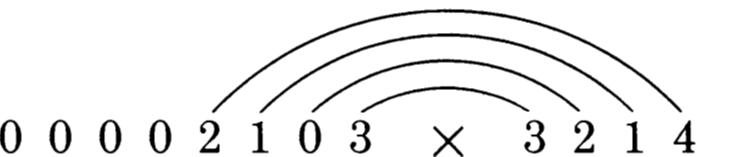
这张图显示了我们计算过程进行到一半时要用到的四对数字。在这一步，我们会说：2*4=8，加上1*1=9，加上0=0，加上9=18。被乘数前导有4个0因为3214有四位。最左边的0用不到，除非在最后一步有进位。我们写下这个数字只是为了可能有用。

请你写出详细的计算步骤吧。

小结

在本章中，我们学习了两位数乘以两位数；然后是大数乘以两位数；然后是被乘数与乘数都是任意长度。在所有这些场景中，我们得到答案最右边一位数字时都是通过两个数字最右边的数字相乘。在所有场景中，我们得到中间的数字都是通过外对和内对相乘然后相加。最后，我们得到答案最左边的数字是通过在被乘数前写上0，然后对这些0同样应用外对和内对连接。前导0的个数和乘数的位数相等。

你应该进行更多的练习，让这些步骤在你的脑海中越来越清晰。以下是一些试题：

• 31 * 23
• 33 * 41
• 63 * 52
• 413 * 24
• 224 * 32
• 705 * 25
• 511 * 61
• 341 * 63
• 4133 * 212
• 31522 * 3131

验算

下面这个验算方法不是特拉赫腾贝格教授发明的，但由于很简单也很方便就被嵌入了他的系统。数学家知道这个方法已经有上百年了，但是对于门外汉来说还比较陌生，也似乎很少在日常生活中使用。出于这个理由我们会将这个方法以“数位和方法”来进行讲述。精髓在于我们将各个数字的数位进行相加，详细解释在下一节。

一个数位是一位数字，从1-9，0也是一个数位。所以任何数字归根到底都是由特定的数位构成的。“数位和”就是我们将某个数字的数位加起来得到的，比如：

数位：4 1 3
数位和：4+1+3=8

但是，在后续的工作中，我们必须理解一点，数位和只有一位数字，如果有必要，我们对数位和再进行一次数位和操作。比如假定数字是6324。我们会得到：

数位：6 3 2 4
数位和：6+3+2+4=15
再做一次：1+5=6

所以，数字6324的数位和是6。换句话说，我们只对一位的数位和进行操作。这么做是因为这让我们的下一步更加简单一些。

乘法的验算中，我们需要找到三个数位和：被乘数的数位和，乘数的数位和，答案的数位和。比方说，我们进行了如下运算并希望进行验算：

\(\frac {00204}{06324} \times 31\)

我们先来找到所有三个数的数位和：

--	数位	数位和
被乘数	2 0 4	6
乘数	3 1	4
答案	6 3 2 4	6

验算原则如下：

答案的数位和应该等于被乘数数位和乘数数位和乘积的数位和。

如果不等，那么计算一定是出错了。在我们的例子中，答案的数位和是6。它应该等于另外两个数位和乘积的数位和。是不是这样呢？我们看一下：6*4=24，24的数位和是6。所以我们验算完毕，答案是对的。

这些数位和的乘法总是很简单的，因为都是一位数。验算可以和原来的计算并行：

\(数位：2\,0\,4 \times 3\,1 = \,\,\,\,6\,3\,2\,4\)

\(数位和：6\,\times4=24=6\)

快捷方式

在对一个数字的数位加和求数位和的时候，有办法省点时间的，特别是对一个很长的数字求数位和的时候。快捷方式如下：

• 在过程中就将中间数字和降到一位数而不要等到最后。比方说你在求252311的数位和。从左开始：2+5+2……自己只记住总和，而这是一个累加和：2，7，9，12……现在要“在过程中降到一位数”。将12变为3。从这个3开始，加上剩下的两位数字：3/4/5。数位和就是5。这要比2+5+2+3+1+1=14，然后从14得到5要简单多了。如果数字特别长，这个方法能节省很多的时间。比如：6889567的数位和是4。在计算过程中进行缩位会是这样的：6/14/5/13/4/13/4/4/15/6/13/4。最后得到数位和是4。不这样做的话，你会一路加到49才行。
• 不用管9这个数字。如果你要加的数字中有9，或者有好几个9，就不用管，不用进行加的操作，最后可以得到一样的结果。这看起来似乎有点古怪，但确实是对的。9399的数位和是3，我们忽略其中的9后可以直接得到。如果你进行加和会得到30，然后还是得到3。更进一步说，如果你正巧注意到两个数字加起来是9，也可以忽略这两个数字：81994的数位和是4，因为8+1=9，而另外两个9不参与计算。只有两个加起来为9的数字相邻或者至少很接近时这么做才是安全的。否则，你可能忘记要忽略某个数字而把这个数字加回去了。

这一验算方法在下一章中会非常有用。你自己想出来的例题中也可以用这样的方法。它也用于乘法以外的其它运算。