1. Word Processor
奶牛Bessie正在完成她的写作课的一篇作文。由于她写字很难看,她决定用一个文字处理器来输入这篇作文。
这篇作文共有N个单词(\(1\le N\le 100\)),用空格分隔。每个单词的长度在1到15之间,仅由大写和小写字母组成。根据作业的要求,这篇作文需要用一种特别的方式排版:每一行包含的字符不超过K个(\(1\le K\le 80\)),空格不计。幸好 Bessie 的文字处理器能够处理这样的要求,它会按照如下的方式:
如果Bessie输入了一个单词,这个单词能够放进当前行,就放在当前行。
否则,将这个单词放到下一行,然后继续向下一行添加单词。
当然,同一行中的单词之间仍然用一个空格分隔。每一行的结尾都不应当有空格。
很不幸,Bessie 的文字处理器刚好坏了。请帮助她正确地排版她的作文!
输入格式(文件名:word.in):
输入的第一行包含两个空格分隔的整数N和K。
下一行包含N个单词,单词之间用单个空格分隔。所有单词的长度都不超过一行中的字符上限数K。
输出格式(文件名:word.out):
输出正确排版的 Bessie 的作文。
输入样例:
10 7
hello my name is Bessie and this is my essay输出样例:
hello my
name is
Bessie
and this
is my
essay第一行包含 7 个非空格字符,包括"hello"以及"my"。再加入"name"会使得第一行包含11>7个非空格字符,所以这个单词会被放到下一行。
分析
这道题难度不大。基本判定如下:
- 读入一个单词,并得到长度。
- 加上目前的行长度。
- 如果不超长,可以在本行输出。
- 如果超长,那就要换行输出。
- 重复1-2的过程。
同时,需要注意的是,根据题设,两个单词之间用空格分割,而且行尾不能用空格。因此在输出时,需要判定是否是第一个单词。
- 如果是第一个单词,那么原样输出。
- 否则,需要输出“
(空格)单词”。
这样能保证题设要求。
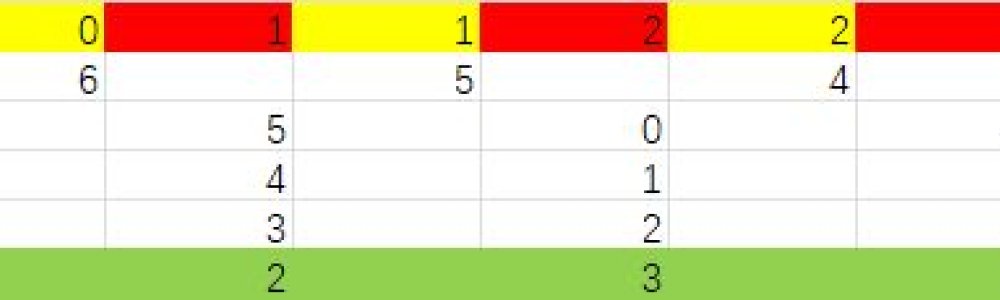
答案
思考
本题很简单。需要注意的点已经在分析中列出。
2. Photoshoot
Farmer John在给他编号为\(1...N\)的N头奶牛排队拍照(\(2\le N\le 10^3\))。FJ一开始计划从左向右数第i个位置排编号为\(a_i\)的奶牛,他在一张纸上写下了排列\(a_1, a_2, ..., a_N\)。不幸的是,这张纸刚刚被Farmer Nhoj偷走了!
幸好FJ仍然有机会恢复他之前写下的排列。在这张纸被偷走之前,Bessie记录了序列\(b_1, b_2, ..., b_{N-1}\),对于每一个\(1\le i\le N\) 满足\(b_i=a_i+a_{i+1}\)。
基于Bessie的信息,帮助FJ恢复可以产生序列b的“字典序最小”的排列a。排列x字典序小于排列y,如果对于某个j,对于所有i<j均有\(x_i=y_i\),且有\(x_j\lt y_j\)
(换句话说,这两个排列到某个位置之前都相同,在这个位置上x小于y)。保证存在至少一个满足条件的a。
测试点性质:
测试点2-4满足\(N\le 8\)。
测试点5-10没有额外限制。
输入格式(文件名:photo.in):
输入的第一行包含一个整数N。
第二行包含N−1个空格分隔的整数\(b_, b_2, ..., b_{N-1}\)。
输出格式(文件名:photo.out):
输出一行,包含N个空格分隔的整数\(a_1, a_2, ..., a_{N-1}\)。
输入样例:
5
4 6 7 6输出样例:
3 1 5 2 4a能够产生b,因为3+1=4,1+5=6,5+2=7,2+4=6。
分析
这道题也有两种做法。复杂度为\(O(N^2)\)的暴力法,以及复杂度为\(O(N)\)的分治法。
暴力法
暴力法的总体分析如下。
由题意可知,\(b[i-1]=a[i]+a[i-1] \to a[i]=a[i-1]+b[i-1]\),这是一个明确的递推关系,我们只要得到\(a[0]\),就可以得出所有的项。
那么我们不妨暴力搜索:\(a[0]\)从最小的值(1)开始,一个个地得到\(a[1], a[2]...\)。这是一个\(O(N)\)的过程。同时由于我们会不断地变动\(a[0]\)(从1到N),这也是一个\(O(N)\)的过程。总体的时间复杂度就达到了\(O(N^2)\)。
另外,对于每次得到的一个序列\(a_i\),我们还要判断是不是不重复地也不遗漏地用完了这N个数。这种查重的工作用集合来处理是最好的。
分治法
分治的思路比较复杂,但想通了以后也是很直白的。
考虑如下的样本输入数据:
6
6 5 4 7 11如果我们从\(a[0]=1\)开始试算,很快就会碰到问题:

第一次试算的时候,我们得到[1, 5, 0, 4, 3, 8]这样一个数列。直觉告诉我们,起步的1太小了,造成下一个数太大(但合理),再下一个数太小(而不合理)……如果我们能一次性调整好出发点,那么我们只要算一次(\(O(N)\))就能得到所有的值。这是我们后续算法的立足点。
一个重要的观察是:第0个数不会造成第1个数的问题,但可能造成第2个数的问题,以此类推;同样的,第1个数会造成3、5、7……这些数的问题。换句话说,偶数位只对偶数位传递着影响,奇数位只对奇数位传递着影响。这两种影响其实是一个,但影响的奇偶位数不会互相干扰。
另外,一个结论是:这些数中肯定会出现一个1。它可能出现在奇数位,也可能出现在偶数位,并都会传递影响。我们要避免的,是因为1的位置不恰当,而造成某些对应位置——如果1出现在奇数/偶数位,则某些奇数/偶数位——的数字出现问题(比如第i位的数字小于等于0)。我们要找出这些位置中最小的那个,让它至少等于1(加上一个正的“偏移量”)。这样一来,这些奇数/偶数位置(以及所有位置)的数字都是合理的了。有了这些数字,我们可以对应地求出其余偶数/奇数位的数字。
我们接下来就要看如何得到相隔为2的位置上,\(a[i-1]\)和\(a[i+1]\)的差值。这个不难。
根据题意,\(b[i-1]=a[i]+a[i-1]\),我们可以得到:
\(\begin{cases}b[i-1]=a[i]+a[i-1] \\b[i]\space\space\space\space\space\space\space=a[i+1]+a[i] \end{cases}\space\space\space\to\space\space\space b[i]-b[i-1]=a[i+1]-a[i-1]\)
也就是说,\(a[i-1]\)和\(a[i+1]\)的差值等于对应的\(b\)数组两个相邻值的差。(下图中的最后一行。)它规定了\(a\)中两两相邻的数字的差。

但是,这个差值不能帮我们决定偏移量。我们注意到,\(diff\)中求出的差值,在每次计算并影响相隔为2的过程中是累加的。所以我们可以用一个前缀和数组来记录累加的影响。注意,在求前缀和时,也要考虑奇偶位不干扰的特性。而这个数组中,对应的最小值就决定了“偏移量”。如果这个最小值是-1,那么我们知道,我们初始设定的1要至少等于2,才能保证这里至少为1(\(1-(-1)\))。

综合考虑上述情况,我们分两种情况:1出现在偶数位;以及1出现在奇数位。
以下我们只分析1在偶数位的情况。
- 计算所有的\(diff\)和\(pref\)数组。
- 找到最小的那个\(pref\)(
min)。 - 假设
1在偶数位(不妨设定在\(a[0]\)),将\(a[0]改为\)1-min$。 - \(a[1]\)可求。
- 递推得到所有后续的数字:$a[i]=a[i-2]+diff[i]。
如果1在奇数位,那么上述过程中的1和2是相同的,不用重复计算,但在做第2步的时候,需要考虑下标起始范围(从0开始还是从1开始)。而3-5中,我们改为先求\(a[1]\),再求\(a[0]\)即可。
这样,我们得到两个可能的排列,分别对应1在偶数位和在奇数位。
接下来,我们只要判定这两个排列的正确性:不能重复不能漏。题目和数据保证这样的排列只有一个。我们输出合理的那个就是了。
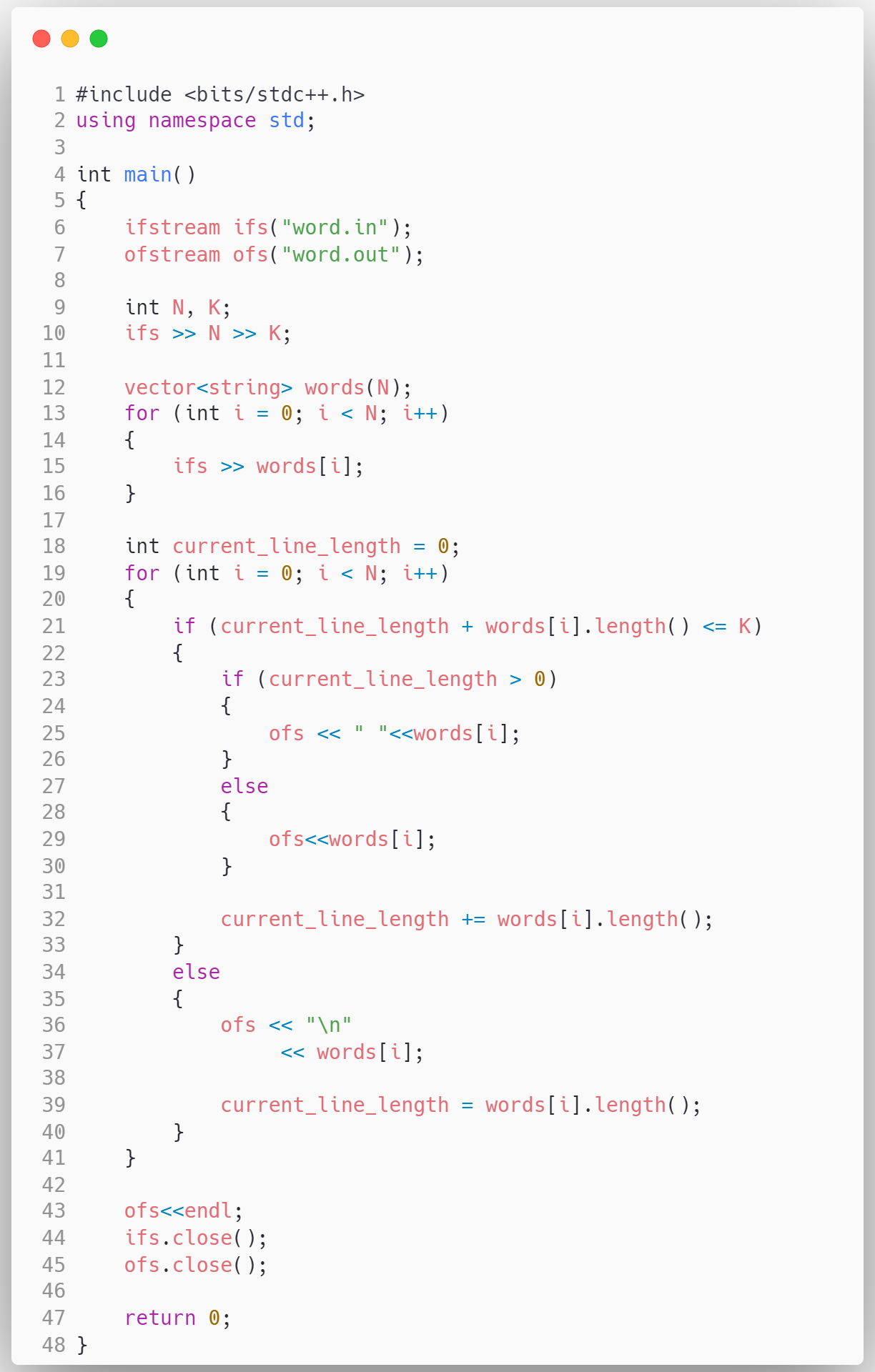
答案
暴力法

分治法

思考
看出暴力法和分治法的差异了么?
暴力法的思路简单,代价是时间长;分治法需要进行深入的分析,找到规律,甚至需要“灵光一现”。这也是两种不同的编程思路:暴力法用的是试错法,一个一个地测试可能的答案;而分治法在分析完毕后,用的是构造法,构造出符合条件的排列——而这正是分治法速度快的原因。
3. Race
Bessie正在参加一场K(\(1\le K\le 10^9\))米的跑步比赛。她从0米每秒的速度开始比赛。在每一秒中,她可以选择将她的速度增加1米每秒,保持速度不变,或者将她的速度减少1米每秒。例如,在第一秒中,她可以将她的速度增加到1米每秒,跑1米,或者保持她的速度0米每秒不变,跑0米。Bessie 的速度不会降低到小于零。
Bessie始终朝着终点线的方向跑,她想要花费整数秒的时间完成比赛(在最后一秒的时候正好跑到终点或者超过终点1)。此外,她不想在终点时跑得太快:在Bessie跑完K米的时刻,她希望她的速度不超过X(\(1\le X\le 10^5\))米每秒。Bessie想要对于N(\(1\le N\le 1000\))个不同的X值知道她多快可以完成比赛。
测试点性质:
- 测试点2-4满足\(N=X=1\)。
- 测试点5-10没有额外限制。
输入格式(文件名:race.in):
输入的第一行包含两个整数K和N。
以下N行每行包含一个整数X。
输出格式(文件名:race.out):
输出N行,每行包含一个整数,表示Bessie完成比赛时的速度小于或等于X的情况下跑完K米需要的最小时间。
输入样例:
10 5
1
2
3
4
5输出样例:
6
5
5
4
4当\(X=1\)时,一种最优方案为:
- 第1秒:将速度增加到1米/秒,跑1米
- 第2秒:将速度增加到2米/秒,跑2米,总计跑3米
- 第3秒:将速度保持在2米/秒,总计跑5米
- 第4秒:将速度保持在2米/秒,总计跑7米
- 第5秒:将速度保持在2米/秒,总计跑9米
- 第6秒:将速度降低到1米/秒,总计跑10米
当\(X=3\)时,一种最优方案为:
- 第1秒:将速度增加到1米/秒,跑1米
- 第2秒:将速度增加到2米/秒,总计跑3米
- 第3秒:将速度增加到3米/秒,总计跑6米
- 第4秒:将速度保持在3米/秒,总计跑9米
- 第5秒:将速度保持在3米/秒,总计跑12米
注意当\(X=3\)时,以下方案是不合法的:
- 第1秒:将速度增加到1米/秒,跑1米
- 第2秒:将速度增加到2米/秒,总计跑3米
- 第3秒:将速度增加到3米/秒,总计跑6米
- 第4秒:将速度增加到4米/秒,总计跑10米
这是因为在Bessie跑完10米的时刻,她的速度是4米/秒。
分析
我们换个思路来思考:题目求的是满足条件的最短完赛时间。如果换个角度会如何:给定一个时间T,以及冲线的速度约束X,Bessie最多能跑出去多少米?
一些直观的结论:
- 比较好的跑法,肯定是在最后一秒的时候以
X冲线。虽然可能多跑了一些距离,但减少了跑不到终点的风险。 - 一般而言,不断加速总是对的,甚至可以超过最终限速,这是为了在同样的时间里跑出更多的距离(反过来说,就是用更少的时间跑完固定的距离),但也因此,需要进行相应的减速。
- 引申一下:Bessie每有一秒钟“超速”,就有一秒“减速”。这样才能保证最终可以回到限速。这就有了一个“已经跑了的距离”和“还要跑的距离”的分别。
- 也因此:每次超速跑过一段距离,就要有另一次以相同的速度跑过同样的距离。
- 跑过的距离+没跑但必然要跑的距离,控制着总距离。如果这个距离超过了输入中规定的距离,就可以保证Bessie在这么多秒内完赛,并满足终点的限速条件。
用图来表示就是(以总共跑10米,终点限速1米/秒为例),Bessie需要6秒完赛:
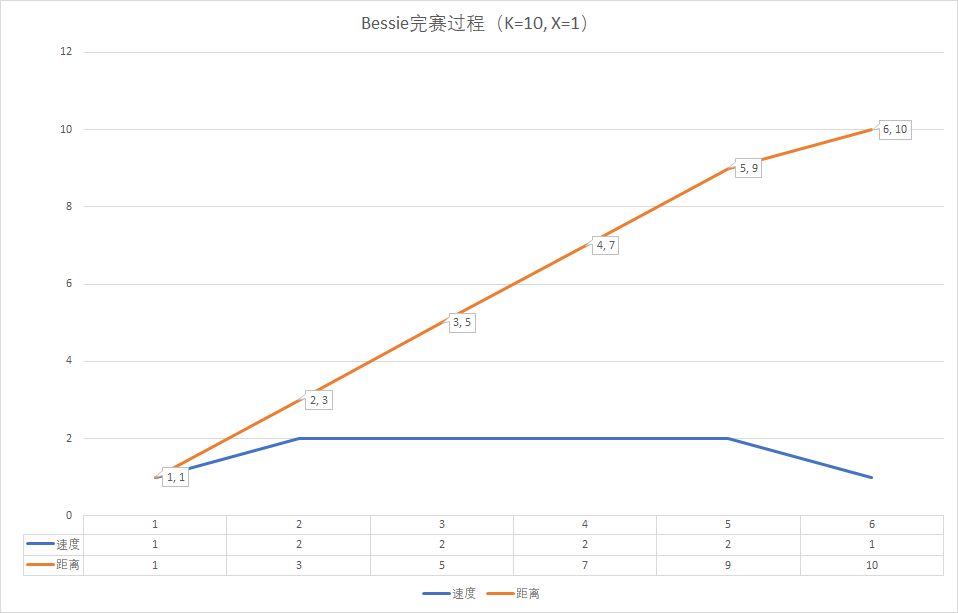
答案
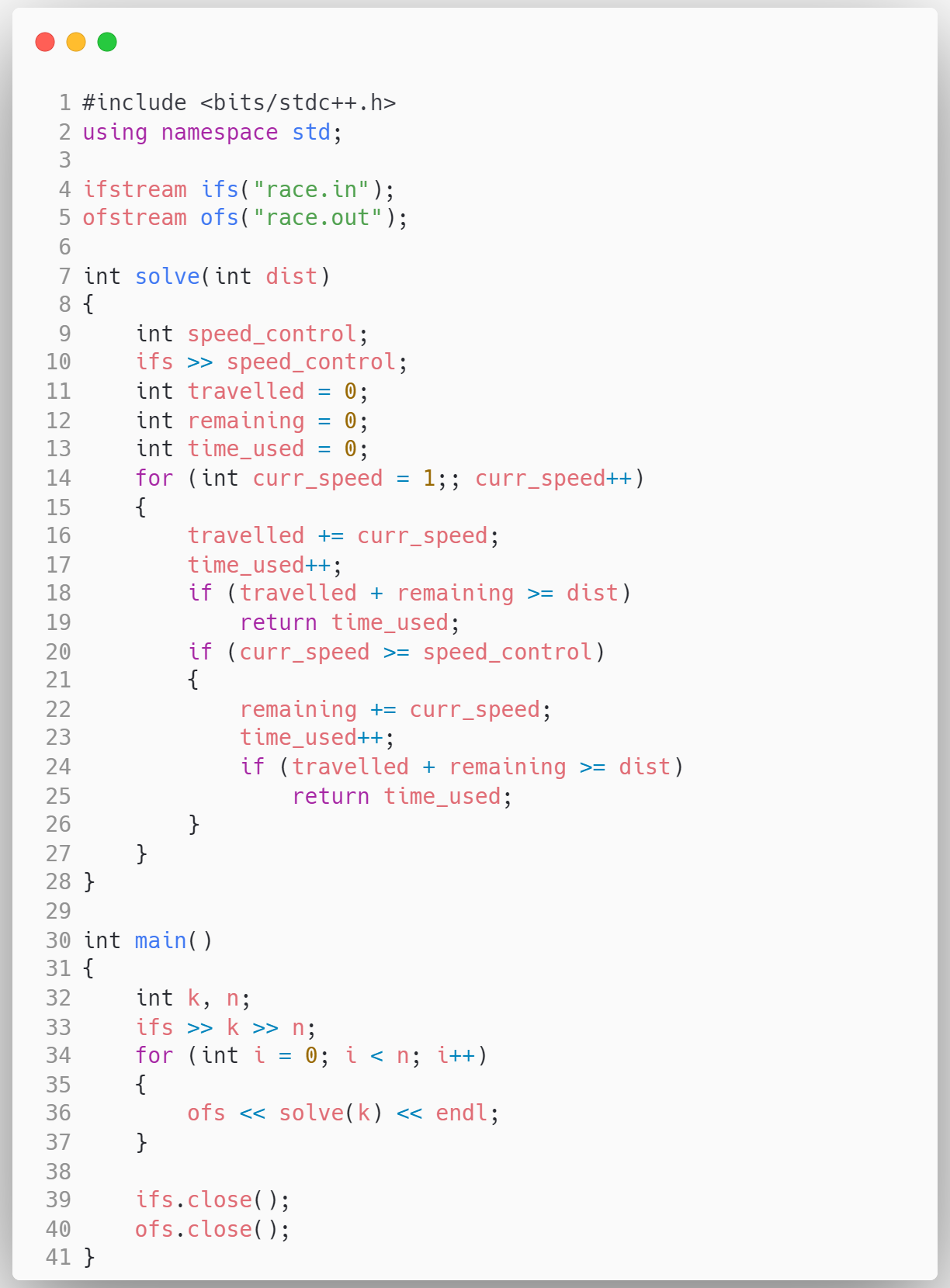
思考
这个解法充分利用了对称性:已经跑了的距离和还没跑的距离之间存在对称,也就是肯定有若干个这样的距离对,是用同样的速度跑完的。通过“同时”减去这些距离,可以很快地求出答案。
-
换句话说,Bessie在最后一秒结束后,总的距离可以超过\(K\)米。 ↩