本页面已浏览28次

1. Social Distancing I

一种新型疾病，COWVID-19，开始在全世界的奶牛之间传播。Farmer John正在采取尽可能多的预防措施来防止他的牛群被感染。

Farmer John的牛棚是一个狭长的建筑物，有一排共N个牛栏（\(2\le N\le 10^5\)）。有些牛栏里目前有奶牛，有些目前空着。得知“社交距离”的重要性，Farmer John希望使得D尽可能大，其中D为最近的两个有奶牛的牛栏的距离。例如，如果牛栏3和8是最近的有奶牛的牛栏，那么\(D=5\)。

最近两头奶牛新来到Farmer John的牛群，他需要决定将她们分配到哪两个之前空着的牛栏。请求出他如何放置这两头新来的奶牛，使得D仍然尽可能大。Farmer John不能移动任何已有的奶牛；他只想要给新来的奶牛分配牛栏。

输入格式（文件名：socdist1.in）：

输入的第一行包含N。下一行包含一个长为N的字符串，由0和1组成，描述牛棚里的牛栏。0表示空着的牛栏，1表示有奶牛的牛栏。字符串中包含至少两个0，所以有至少有足够的空间安置两头新来的奶牛。

输出格式（文件名：socdist1.out）：

输出 Farmer John以最优方案在加入两头新来的奶牛后可以达到的最大D值（最近的有奶牛的牛栏之间的距离）。

输入样例：

14
10001001000010

输出样例：

2

在这个例子中，Farmer John可以以这样的方式加入奶牛，使得牛栏分配变为10x010010x0010，其中x表示新来的奶牛。此时D=2。不可能在加入奶牛之后取到更大的D值。

分析

基于现有的牛栏分配情况（也就是输入），我们可以计算出当前的所有间距：\(l_1, l_2, ..., l_k\)。

直觉告诉我们：

• 第一头牛只有三种可能的位置：最左边、最右边、最大的间距的中间位置。
• 第一头牛就位后，第二头牛也有三个可能的位置：最左边、最右边、最大的间距的中间位置。

这个组合只有9种不同的可能，遍历是可行的。但这九种不是全部的放置方式。还有一种方式，是某个间距很大，可以让这两头牛“均匀”地分布在这个间距中。这样一来，一共有10种可能的放置方式。可以证明，可能的放置方式就是这10种。

我们需要一些辅助函数。

最大的间距以及起始位置

这个函数难度不大。需要注意的是，每个1都会被用到两次：一次作为终点，下次作为起点。

最小的间距

这个是我们的目标。我们的目标是这个值尽可能大。

在最大的间距中均匀地放牛

这个很简单。

只要最大间距大于等于2，就一定可以放一头牛，而保证这三头牛中还有两头的间距为1。因此，新的最大的最小间距只能为1了。而如果最大间距居然只有1，那我们不能放在这里。因为这意味着将最大的最小距离变为了0，而不放这里反而可以为1。

在最大间距中放一头，然后再在新的最大间距中放一头

这个是必须考虑的。

答案

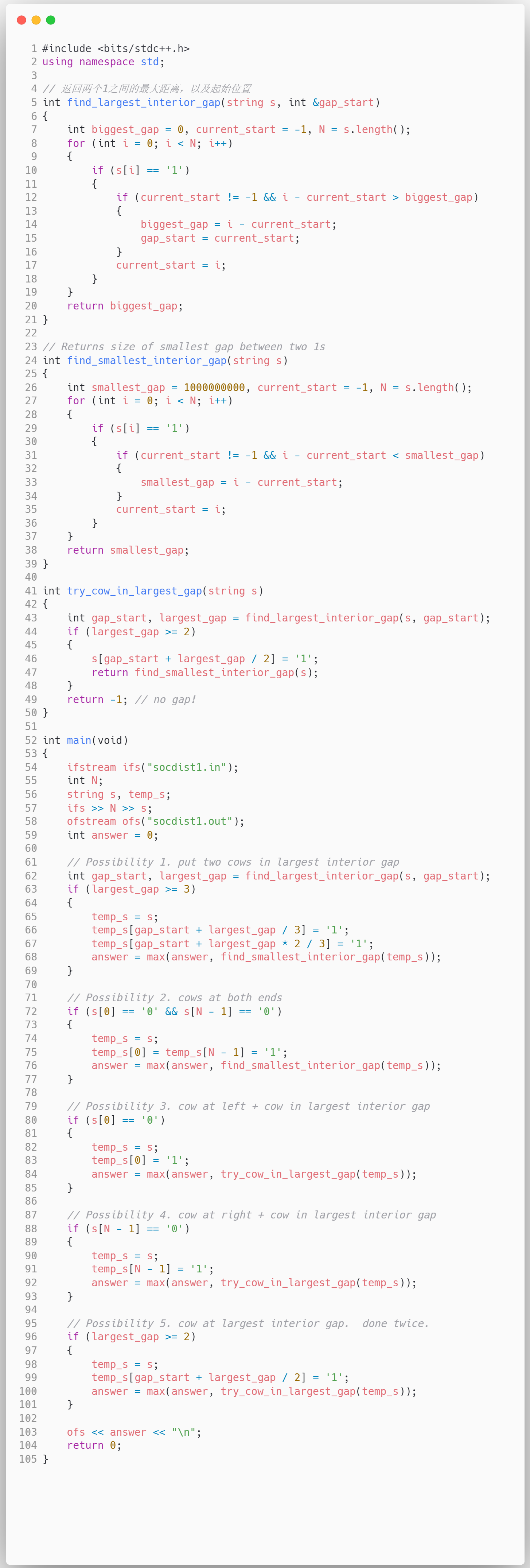
思考

这道题目的关键，是找到所有可能的放置方式。算法本身难度不大。

2. Social Distancing II

由于高传染性的牛传染病COWVID-19的爆发，Farmer John非常担忧他的奶牛们的健康。

尽管他尽了最大努力使他的N头奶牛们（\(1\le N\le 1000\)）践行“社交距离”，还是有许多奶牛不幸染上了疾病。编号为\(1 ... N\)的奶牛们分别位于一条长直道路上的不同位置（相当于一维数轴），奶牛i位于位置\(x_i\)。Farmer John知道存在一个半径R，任何与一头被感染的奶牛距离不超过R单位的奶牛也会被感染（然后会传染给与其距离R单位内的奶牛，以此类推）。

不幸的是，Farmer John并不确切知道R的值。他只知道他的哪些奶牛被感染了。给定这个数据，求出起初感染疾病的奶牛的最小数量。

输入格式（文件名：socdist2.in）：

输入的第一行包含N。以下N行每行用两个整数x和s描述一头奶牛，其中x为位置（\(0\le x\le 10^6\)），s为0表示健康的奶牛，1表示染病的奶牛，并且所有可能因传播而染病的奶牛均已染病。

输出格式（文件名：socdist2.out）：

输出在疾病开始传播之前已经得病的奶牛的最小数量。

输入样例：

6
7 1
1 1
15 1
3 1
10 0
6 1

输出样例：

3

在这个例子中，我们知道\(R\lt 3\)，否则位于位置7的奶牛会传染给位于位置10的奶牛。所以，至少3头奶牛初始时已被感染：位于位置1和3的两头奶牛中的一头，位于位置6和7的两头奶牛中的一头，以及位于位置15的奶牛。

分析

这个问题，R的判定很重要。一般来说，R越大，一开始被感染的牛的数量就越少。但是，基于给出的最终状态，这个R不会超过一头感染的牛和一头健康的牛之间的最小距离。例如，按照题目中给出的样例数据，这个R不超过3。

这也是我们需要编写的一个函数。

找到R之后，我们要找到连续一群感染牛的数量。“连续一群感染牛”指的是，这一组里全是感染牛（可以有没有牛的空牛栏），但这一组位置的前一个和后一个都是健康牛。在上图中，1-9和11-15是满足条件的两组。这些组中都至少要有一头牛一开始就被感染。

同时，这些组中，如果两头感染牛的距离超过了R，那就需要再多一头初始被感染的牛。上图中，就是3和6这样的情况。

这两种情况的感染牛的数量加起来就是答案。这是我们需要编写的另两个函数。

答案

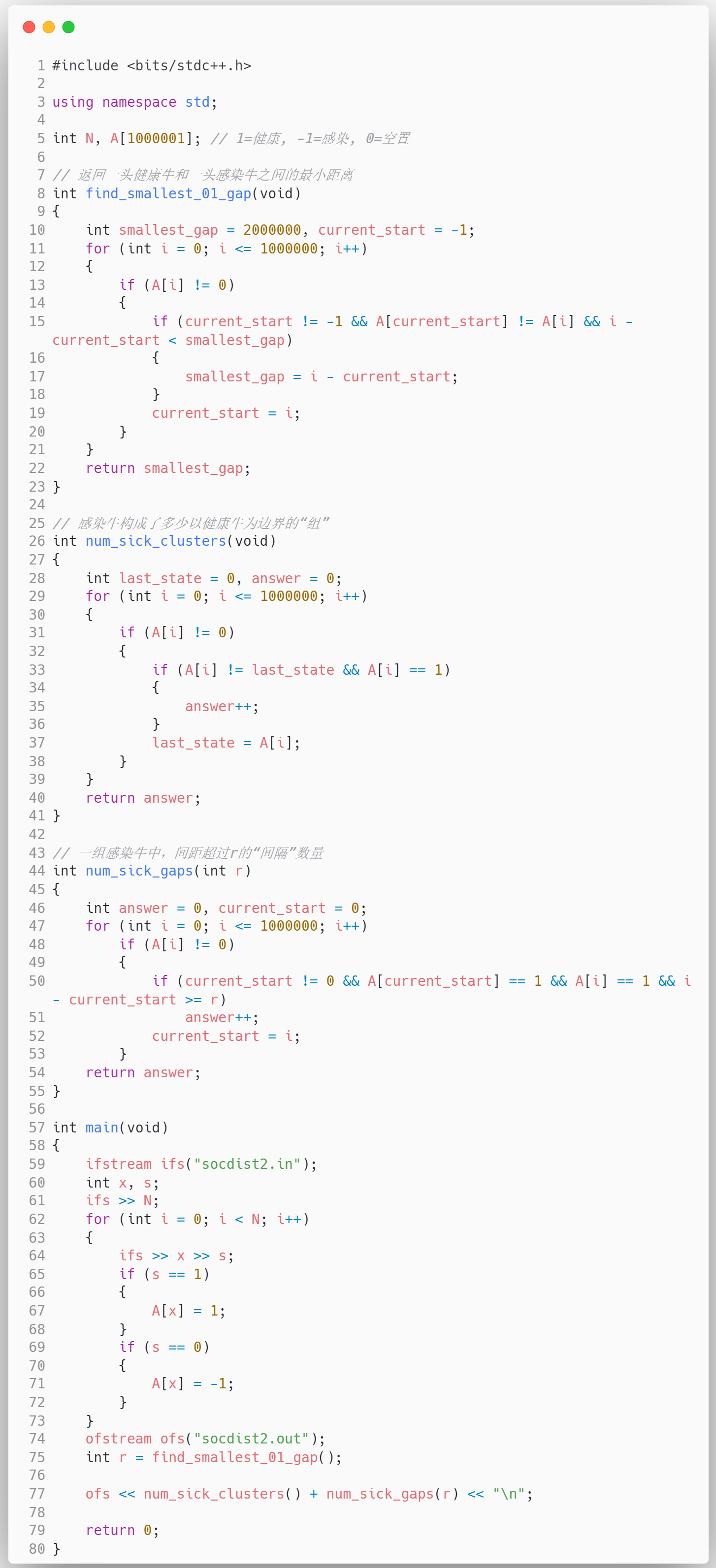
思考

试着在上述程序中打印出各个关键值，看看是不是和你的判断一样？

3. Cowntact Tracing

由于高传染性的牛传染病COWVID-19的爆发，Farmer John非常担忧他的奶牛们（编号为\(1 ... N\)）的健康。

最近，Farmer John对他的所有奶牛进行了检测，发现有一部分奶牛对该疾病的检测结果呈阳性。利用牛棚内的视频监控，他得以查看最近的奶牛之间的互动行为，结果发现奶牛们互相打招呼时，她们会握蹄，不幸的是这是一种会将疾病从一头奶牛传播给另一头奶牛的行为。Farmer John汇总了一个添加了时间戳的清单，每条数据的形式为(t, x, y)，表示在时间t，奶牛x与奶牛y握了蹄。Farmer John同时还知道以下信息：

• （一）他的农场上恰有一头奶牛最初带有携带疾病（我们将这头奶牛称为“零号病人”）。
• （二）一旦一头奶牛被感染，她会在接下来的K次握蹄中传染疾病（可能会与同一头奶牛握蹄多次）。握蹄K次后，她不再在此后的握蹄中传染疾病（因为此时她意识到了她会传染疾病，于是会仔细地洗蹄）。
• （三）一旦一头奶牛被感染，她会持续处于被感染状态。

不幸的是，Farmer John 不知道他的N头奶牛中的哪一头是零号病人，也不知道K的值！基于他的数据，请帮助他缩小这些未知量的范围。保证至少有一种可能的情况。

输入格式（文件名：tracing.in）：

输入的第一行包含N（\(2\le N \le 100\)）和T（\(1\le T\le 250\)）。下一行包含一个长为N的字符串，每个字符均为0或1，表述目前Farmer John的N头奶牛的状态：0表示一头健康的奶牛，1表示一头染病的奶牛。以下T行每行包含Farmer John的互动清单中的一条记录，由三个整数t、x和y组成，其中t为一次互动发生的正整数时间（\(t\le 250\)），x和y为范围\(1 ... N\)内的不同整数，表示时间t握蹄的两头奶牛。在每一时刻至多只有一次互动发生。

输出格式（文件名：tracing.out）：

输出一行，包含三个整数x、y和z，其中x为可能为零号病人的奶牛数量，y为与数据一致的最小可能K值，z为与数据一致的最大可能K值（如果通过数据无法推断K的上界，z输出Infinity）。注意可能有\(K=0\)。

输入样例：

4 3
1100
7 1 2
5 2 3
6 2 4

输出样例：

1 1 Infinity

唯一可能是零号病人的是奶牛1。对于所有的\(K\gt0\)，奶牛1在时刻7感染奶牛2，而奶牛3和奶牛4均不会被感染。

分析

这道题可以考虑暴力求解。我们看一下时间复杂度。一共有N头牛。而根据输入的T来找到K的话，需要遍历所有的T，并在每次遍历时都要从0开始到T地模拟传染过程。所以总的时间复杂度是\(O(NT^2)\)。代入上限，我们得到：\(100*250*250=6,250,000\)。这个数值还算可以。

模拟传染的过程也很简单：根据给出的社交关系以及假定的零号病牛，一次次地模拟传染过程，到最后，如果传染的牛和给出的结果一致，我们就可以认为这头牛就是零号病牛（计数加1）。同时，在这模拟过程中，根据每一次传播的时间，我们可以得到K的估算。这个也是核心过程。我们再深入分析一下，这个过程的伪代码如下：

function simulate_and_check_consistency(患者0, K)
    // 初始化数组
    用infected[101]保存本次模拟结果，初始化为false
    用num_handshakes[101]保存传染次数，初始化为0

    // 标记初始感染的牛
    infected[患者0] = TRUE

    // 模拟时间上的握手
    t从0到250的循环: 
        // 获取在时间 t 参与握手的牛
        x = cowx[t]
        y = cowy[t]

        // 检查握手是否有效
        如果 x > 0 则
            如果牛 x 感染，则增加握手计数
            如果牛 y 感染，则增加握手计数
            如果牛 x 感染且握手计数在限制内，则感染牛 y
            如果牛 y 感染且握手计数在限制内，则感染牛 x
        结束判定
    循环结束

    检查最终感染状态是否与预期状态匹配，如果有一个地方不匹配，返回false；
    全部匹配，返回true。
    //这表明，这一次的模拟是“成功”的，也就是说：
    //这个患者0在这个K值下，以给出的握手过程，可以达到最终的传染状态

这里判定的关键是：一头牛感染了，而且在传染次数（K）以内，才会传染给另一头牛。

答案

思考

本题难度不大，想清楚复杂度后，就可以发现暴力法是可行的。

模拟过程是本程序的核心，它的算法也很简单明了。看似“复杂”的问题，认真分析后，会发现也许不那么“复杂”。