本页面已浏览332次

笛卡尔（René Descartes，1598-1650）——生平与成就

热内·笛卡尔出身显赫，其家族为法国文化做出了卓越的贡献。他的父亲尤金出身于医生世家，而其父本人是布列塔尼行省议会议员。他的母亲珍妮（娘家姓布罗夏德）出身于一个富裕的家庭，在普瓦图有产业。两人于1589年成婚并已育有一子名叫皮埃尔，一女名叫珍妮。他们的三子热内生于1596年。为他取名热内是为了纪念其祖父热内，后者于1596年去世。

笛卡尔对他母亲没有什么印象，因为她在诞下他13个月后就因难产而去世了。他的父亲将孩子们留给一位叫做珍妮·尚的女士照料¹，而后者也因此成为他的养母，即使笛卡尔的父亲在1600年再婚后亦如是。

要说笛卡尔心目中的母亲形象是珍妮·尚，那么他心目中的父亲形象就应该是埃蒂安·沙莱神父，拉弗莱彻地区耶稣会学院的校长。笛卡尔在1606年入学该校并在该校学习了八年。该校开始招生也就是在两年前。

和当时法国那些由政府机构运作的大学——它们明确地基于人文主义构建——不同的是，诸如拉弗莱彻这样的教会大学仍然会基于传统教会思想和古代经典的坚实基础。和大多数法国大学一样，拉弗莱彻是中学和大学的结合体。在拉弗莱彻的第一年是预备课程，接下来三年是语法（拉丁语和希腊语），第五年是修辞学。所有课程均已拉丁语传授。虽说耶稣会的神父对学生的学业要求非常严格，但是也都有着慈悲心怀。由于少年笛卡尔身体不好，拉弗莱彻的神父也经常允许他整个早上可以卧床休息。

前五年结束后，很多学生会离开诸如拉弗莱彻这样的耶稣会学院，而申请进入另一所大学，而其修习的专业无非下列三种主要专业之一：法律，医学和神学。事实上，大部分所谓世俗学校会拒绝招收那些在耶稣会学校呆了超过5年的学生，他们担心的是这些学生被灌输了太多相对较新的也较激进的耶稣会教义。笛卡尔没有这么选择。他听闻其父亲希望他在拉弗莱彻再呆三年时，是很开心的。

接下来的四年，笛卡尔开始学习形而上学，伦理学，自然哲学以及辩证法。自然哲学的课程包括学习欧几里德，阿基米德以及丢番都，还有当代数学。在拉弗莱彻期间，笛卡尔和一个人建立了私人关系，这一关系已经被证明与他在学校里获得的数学基础一样有价值。笛卡尔后来与之通信的人中有一位梅森²，他也是拉弗莱彻的学生。1620到1640年期间，梅森就像法国科学界活动的中继站，他和所有哪怕只有一丝影响力的人保持通信。他的通信记录就超过1万页。

笛卡尔于1614年离开学院，并进入附近的普瓦捷大学学习法律。两年后他获得法学学位。但是，他对法律似乎兴趣寡然。虽然他父亲肯定希望他从事法律事务，但是笛卡尔从来没有这方面的任何记录。他在普瓦捷真正的兴趣是医学，并对解剖学产生了浓厚的兴趣。

在法国的同一个地方度过了生命中最早的20年后，笛卡尔必定是很想看看欧洲的其余地方。获得法学学位后，笛卡尔加入了拿骚的莫里斯亲王的部队，担任文职官员。在荷兰呆了两年半后，笛卡尔离开了莫里斯亲王，转而加入了巴伐利亚的马克西米兰的军队。不久，笛卡尔来到法兰克福，并见证了费迪南二世加冕为神圣罗马皇帝的准备工作。

笛卡尔继续其军旅生涯直到他30岁那年。三十年战争爆发时，他在17世纪20年代的前半段游历了欧洲。他的通信记录着这些年中，他访问了巴伐利亚，波西米亚，德国，意大利以及匈牙利，还有荷兰以及法国。尽管这几年他一直在旅行，笛卡尔还是抽出时间为其形而上学、认识论以及自然哲学的工作打下了基础。1618年，他在为奥朗热的莫里斯服役期间，认识了比他大7岁的荷兰人比克曼。和笛卡尔一样，比克曼也对哲学和数学感兴趣。

比克曼成为笛卡尔的另一个父亲似的形象，而笛卡尔也成为比克曼的知识学徒。最重要的是，比克曼成为笛卡尔的密友。1619年，笛卡尔23岁生日前不久，他在写给比克曼的一封信中列出了一种新数学的纲要：

我想呈现给大众的是……有着全新基础的科学，使得我们能回答所有能以任何类型——不论其连续或不连续——的数量表达的问题，而每个问题都是符合其本质的。在算术中，某些量可以用有理数解决，有些要靠无理数，而有些只能想象而不能解决。籍此，我希望证明，在连续量的情况下，某些问题可以仅用直线和圆来解决；有些可以仅用圆之外的曲线来解决，而这些曲线可以由单一行为产生，并用一种新的圆规画出。这种新的圆规，我不认为会比我们通常用来画圆的圆规更不精确，而且一样的几何化。而最终的那些问题的解决，要靠产生的曲线（但是他们的行为互相间不从属）——那些显然只能靠想象的曲线，比如割圆曲线就是为人熟知的。我不认为，我们可以想象出什么东西而不能用类似的轨迹去解决：事实上，我希望能表明，某些特定类型的问题能用某种方式解决而不能用另一种，从而在几何学方面将不几乎不再有什么可以发现的东西。只是一个无穷尽的任务，一个人无法完成。它令人难以置信且野心勃勃。但我既已得见此门科学之重重黑暗中之些许曙光，籍此必能拨开层层乌云。

这一段话可以认为是后来成为笛卡尔《思维指引之规则》这一著作中某一部分的首稿。

很明显，哪怕一个人只受到过最低限度的教育，他都会知道哪些可以归为数学，而哪些在任何情形下都不能归为数学。在我更进一步地研究这一问题后，我发现，数学唯一的着重点就是关于顺序或者量度的问题，而不论这一测量的问题牵涉到数、形状、星星、声音或者其它什么物体。我意识到，一定有一种通用的科学可以解释这一切——可以用顺序或者量度提出的一切而无关主体。这一种科学应以mathesis universalis（“普遍数学”）来表述。这个单词如此神圣却又含义明细，因为它包含了一切，因此其它的科学得以被成为数学的分支。在可用性和简单性方面，对比那些从属的科学来说，它是如此杰出，因为有着这一明显的事实：它包含了它们所处理的所有东西……一直以来，我将我所有的精力都投入到了普遍数学之中，以期我能在适当的时候处理更先进的科学。

等到笛卡尔真正有时间研究他的数学时，已经过去了将近二十年。笛卡尔的军旅生涯结束后，他于1625年到1628年间住在巴黎。他发现他所处的思想家圈子和他一样，都非常拒绝亚里士多德式的正统理论，这些理论在17世纪早期还是有着上升态势。时不时地，他和他的圈子会讨论哥白尼日心说的好处。但是他们需要用假想的属于来进行其讨论。1624年，位于巴黎的索邦神学院发布了一条法令，任何人如果散播那些与所传授的并经批准的古代作家之观点相悖的言论，将有被处死的危险。

笛卡尔一生都是一个热诚的天主教徒，但是他觉得巴黎的知识氛围已经处于教会影响之下，过于危险。于是在1628年他前往更自由的环境：新教徒治下的荷兰。他为了捍卫某位女士之清誉而要进行的一次决斗也应该是加快了他离开巴黎的决定。对于这位女士我们一无所知，只知道笛卡尔将她的美丽与真理之美相提并论！他离开巴黎的时候一定是很匆忙的。笛卡尔的书信中提到他什么都没有带，只带了圣经和圣托马斯·阿奎那的《神学大全》（Summa Theologica）。

笛卡尔定居在阿姆斯特丹并很快在当地的知识圈内确立了其卓越的地位。1634年冬到1635年冬，笛卡尔成为波西米亚女王，帕拉丁选帝后伊丽莎白·斯图亚特宫闱中的常客。她是波西米亚的腓特烈五世的遗孀。他的军队在1620年³的白山之战中被击溃，因此不得不流亡到了荷兰。腓特烈于1632年去世后，他的遗孀继续住在和朗，依靠其弟弟英格兰国王查理一世提供的年金生活。笛卡尔和伊丽莎白女王有很密切的知识上的交往，后来和她女儿波西米亚的伊丽莎白公主也是如此。

笛卡尔在阿姆斯特丹期间，与康斯坦丁·惠更斯成为朋友。惠更斯当时是奥朗热亲王腓特烈·昂利的秘书。惠更斯出生外交世家，并成为笛卡尔忠实的支持者。不过惠更斯家族最为人所知的是康斯坦丁的长子克里斯蒂安（1629-1695），一位与牛顿同时代的伟人。英国哲学家洛克将他称为“惠更思”⁴。笛卡尔对年经的克里斯蒂安·惠更斯的教育积极参与，而惠更斯则发展了笛卡尔的涡流理论。

17世纪30年代中，笛卡尔一生中唯一的一次罗曼蒂克的经历发生了，女方叫伊莲娜，是他所住屋子里用的女仆。1635年7月，她为笛卡尔生下一个女儿，他们将她取名为弗朗辛并将孩子受洗为新教徒。而在她短暂的一生中，孩子和他父亲也只有几次接触。1640年她过完五岁生日后不久，就被当时席卷整个荷兰的猩红热夺去了生命。她的死深深触动了笛卡尔。弗朗辛死了，而此时笛卡尔才意识到她对他意味着什么。按照当时的习俗，在孩子去世后，笛卡尔就再也没有和伊莲娜联络过。

荷兰还是笛卡尔最伟大的著作《方法论》、《第一哲学沉思集》、《哲学原理》、《几何》等的诞生地。这些书本篇都有节录。

通过他对两个非常基本的数学运算：确定积和平方根的阐述，我们可以很容易地看出笛卡尔数学方法的力量。回忆一下欧几里德以及他之后直到16世纪的数学家的做法，算术命题的表述通过集合形状（比如线段长度）进行，而这不是因为线段长度提供了一个很好的方法来表达数字，而是因为数字本来就是长度！于是，要确定两个抽象值X和Y的乘积就意味着构建一个边长为X和Y的长方形并求出以这个长方形面积来表示的两数的乘积！与此类似，古人求一个抽象值X的平方根的时候，会将X表示为一个两维的图形，并找到一个正方形与之面积相等。这个正方形的边长自然就是X的平方根。

无理数危机逼得希腊人求助于这些几何解释。笛卡尔可没有这些几何上的限制：

我们应该注意到，这些构成连续序列的比例，应该理解为用数字表示的关系。其它人试图用一些不同的维数和形状等常规的代数术语来表示这些比例。他们管第一个叫根，第二个叫平方，第三个叫立方，第四个叫双二次方，以此类推。我必须承认，这些表述长久以来都误导了我……这些名字都该被废止，因为它们必定会在我们的思维中引起混淆。理由是，尽管一个量可以用立方或者双二次方来表述，但绝不应该在想象中被表示为除了直线或者平面之外的形象……最要紧的是，我们需要注意，根、平方、立方等等都只是连续比例的量，也就永远蕴含着我们上一个原则中谈到的自由选取的单位。

因此，一个数量x的立方（表示为\(x^3\)），不是因为它代表了一个几何上的立方体（一个三维的形状），而是因为它代表了由三个关系构成的一系列比例：

\(1:x=x:x^2=x^2:x^3\)

笛卡尔没有为这些考虑的对象而要求去构建一个几何形体，他假定所有这些给定的对象是存在的，并证明如何借助线段来构造这些值。

在《几何》的开篇，他这样来确定两个数量的乘积。他假设单位量（1）已经由线段AB给出，然后来求由线段BD（和AB重合）和线段BC的乘积。他将点A和点C连接，然后过D点作AC的平行线，与BC交于E。

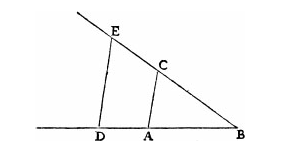
如此一来，笛卡尔创建了两个相似三角形ABC和DBE。因此它们的边是成比例的：

BE:BC=BD:BA

而既然BA=1，得到：

BE:BC=BD

也就是：

BE=BC*BD

这就是答案。

取平方根也一样简单。他令线段GH代表要求平方根的数值，将其从G延长到F，使得FG为单位量。之后，他等分线段FH，中点为K。以K为圆心，KH（=KF)为半径做一个半圆。从G点引出FH的垂线并与半圆交于I点。

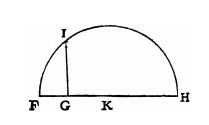
这一次，笛卡尔实际上构造了三个相似直角三角形IGF，HGI，HIF。（这三个都是直角三角形。）由于IGF和HGI相似，我们得到：

GH:GI=GI:FG

根据假设

FG=1

因此得到

GH=GI*GI

也就是说，GI是GH的平方根。

笛卡尔直到1648年都一直住在荷兰。此时，瑞典的克里斯蒂娜女王为笛卡尔提供了一个位于她斯德哥尔摩宫廷的一个职位，要他为学者们建立一所学院，并教授她伦理学和神学。笛卡尔接受了这个邀请，而女王派出了一艘战船将他接到了瑞典。笛卡尔从未受过如此皇家恩宠，他大概也想象着在瑞典宫廷中会受到同等礼遇。虽然他的周遭都是皇室成员，但笛卡尔从未屈尊到去打听一下他要遵守的时间表是怎样的。

笛卡尔一生孱弱，经常会在床上呆个一早上。令他懊恼不已的是，他终于得知这不是瑞典宫廷的生活方式。女王坚持早上5点上课，而不论天气如何。这就使得笛卡尔要在4点半离开寓所，鼓足勇气迎接那时暴雪肆虐的北方天气。1649到1650年间的冬天特别难捱，笛卡尔不久便患上了肺炎。笛卡尔不相信女王医生给出的治疗方法，而更偏好自己的那一套。他试着灌以酒和烟草的混合饮料来给自己治病，而这能让他咳出痰液。很快他的病情就恶化了，谵语连篇。两天后的1650年2月11日，他离开了人世。