本页面已浏览160次

勒贝格（Henri Lebesque，1875-1941）——生平与成就

我记得听过这么一个故事。有一位巴比伦天文学历史学家，有次他的同事请他帮忙解读一份古天文学手稿。他摸了一会胡子，开始仔细观看他同事放在他面前的手稿上的古老符号。突然，他将手稿转了90度，从竖直变成了横放，开始向同事解释手稿的意义。勒贝格在积分理论方面也做出了这样的一个改变。

1875年6月28日，勒贝格出生在巴黎以北约50英里的博威镇上的一个中产阶级家庭。他的家庭崇尚知识方面的追求。虽说他的父亲只是个排字工人，母亲是一个小学老师，但是家里却有一个了不起的图书馆，让勒贝格可以有宽广的阅读范围。当地政府很快意识到他的才华，并在他父亲死于肺结核后，安排一位当地的慈善家资助他的教育。

勒贝格学习成绩突出。他先是在当地的博威学院，然后进入巴黎的圣路易公立学院，再是路易大帝学院。1894年他19岁那年，他入学著名的巴黎高等师范学院。在学院里，勒贝格通常沉浸在数学中，而忽略那些他不那么感兴趣的学科。他的日记中表明，他在一次化学考试时，他不在黑板上写任何东西，只是对着考官——考官听力不好——用很低的声音说话，这样通过了考试！

1897年勒贝格从高等师范学院毕业。毕业后的两年，他在学院的图书馆工作并开始研究测量和积分的新理论，此时他在巴黎大学进行研究生学习。勒贝格获得了靠近德国边境南锡中心学校的一个教职。也正是在南锡，勒贝格完成了研究，其结果成了他的毕业论文，并于1902年获得巴黎大学博士学位。米兰的《数学年报》立即加以发表，并被称为具有革命性的突破。

在勒贝格之前，数学家认为黎曼已经将积分理论研究到了极致。在之前的章节中，我们已经看到，柯西和黎曼的积分理论基于这样的一个过程，即分割x轴，并在每个区间上的某处取函数\(f(x)\)的值。

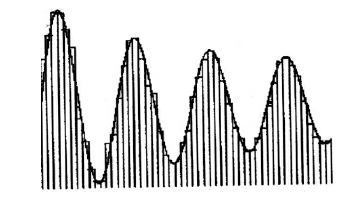
勒贝格的伟大创举在于他不分割x轴，而是分割y轴——分割方法和柯西及黎曼分割x轴的方法类似。

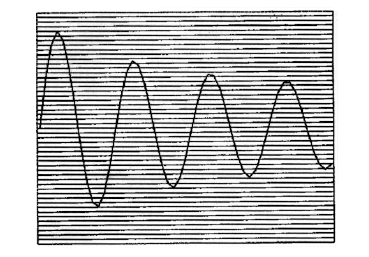
分割好y轴后，勒贝格于是考虑区间的每个元素，并进而处理x轴上待积分的函数映射到的区间的那个元素的量度。

举个例子。考虑区间\((y_n, y_{n+1})\)，这是y轴上的一个分区。

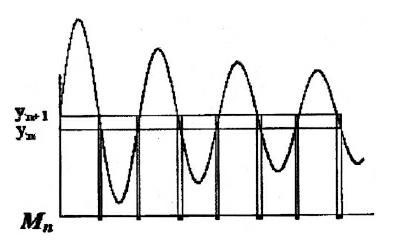
在本例中，x轴上取值在区间\((y_n, y_{n+1})\)的那些x值构成集合Mn。为了确定区间\((y_n, y_{n+1})\)对我们要计算的勒贝格积分的贡献，勒贝格将Mn的量度乘上区间\((y_n, y_{n+1})\)内的任意一个值。利用魏尔斯特拉斯严格的ε-δ方法，勒贝格说如果y轴上的区间“最宽”的元素尺寸趋向于0时，极限存在，那么该极限就是我们所讨论的勒贝格积分的值。

通过这样来定义积分，将积分理论约简为测量理论。如果我们从几何角度来看这个问题，我们就能看出勒贝格将确定一个二维对象面积的问题简化为确定一个点的集合的亮度问题，而这些点位于一条一维的实线上。在勒贝格富有创意的论文中（本文选录了其大部分），他先是讨论测量位于一条一维直线上的点的集合的问题，然后开始讨论他的积分理论。

勒贝格先是声明，为了满足我们的直觉一个量度必须具备的特性：

• 区间[a, b]（也就是所有满足\(a \leq x \leq b\)的实数x的集合）的量度就是\(b-a\)。
• 如果实数En的集合都不交（亦即，两个集合没有任何共同的点），那么En的并集的量度等于各个En的量度的和。
• 如果一个实数集En的量度为m，那么对E内每个实数加上一个常量a（记为E+a）得到的点集的量度还是m。

在定义集合的量度之前，勒贝格先定义它的外量度和内量度。如果一个集合有外量度和内量度，且两者相等，那么集合的量度也就等于这个值。

一个集合的外量度是这样定义的：它是构成要测量的集合的超集的区间覆盖的集合的量度，也就是说要测量的集合是构成覆盖的区间的并集的一个子集。每个覆盖中的区间都有一个量度，这些量度的和可能是有限的。因为一个有界的集合总能被整个包围它的区间覆盖，于是勒贝格意识到一个有界集合的覆盖量度之和总有一个有限的下限值。这个下限就是这个集合的外量度。

通过使用康托的证明（即，有理数可以枚举，而且可以将第n个有理数包围在一个闭区间中，所以量度为\(\epsilon ^n\)），勒贝格证明，有理数的外量度为0。将所有这些区间的量度相加得到ε，而ε可以无限小。因此，有理数的外量度为0，有理数就是一个量度为0的可测集。

对于由区间[a, b]包围的集合E的内量度，勒贝格是这样定义的，它等于包含在[a, b]区间内的点集减去包含在E中的点集得到的集合的外量度。也就是说，一个由[a, b]区间包围的集合E的内量度，等于区间[a, b]的量度，减去区间[a,b]内包含的点集减去集合E中包含的点集得到的集合的外量度。其公式是：

\(meas_i(E)=b-a-meas_e([a,b]-E)\)

其中，i下标表示内量度，e下标表示外量度。

按照勒贝格的定义，很明显的，位于单位区间[0, 1]之间的无理数集合的内量度为1，因为单位区间[0, 1]内有理数集合的外量度为0。立即可以得到的结果是：[0, 1]单位区间中无理数集合的量度为1，而有理数集合的量度为0。

利用这个截然不同的处理积分理论的方法，好多函数变成可积，并可以加以数学分析。最明显的一个勒贝格可积而黎曼不可积函数的例子是Χ(x)，即实数范围内数值有理性的特征函数。它取值如下：

• Χ(x)=1，如果x是有理数
• Χ(x)=0，如果x是无理数

这个函数是黎曼不可积的，因为x轴上的每个区间，无论有多么小，都包含无穷多个有理数和无穷多个无理数。因此，黎曼求和无法收敛。相反，区间内唯一对确定勒贝格积分有作用的元素是那些取值为0和1的元素。我们已经看到，Χ(x)取1的时候，那些映射到x轴上的点集的量度为0，而任何区间上无理数的量度是区间的宽度。因此Χ(x)在任意区间[a, b]上的勒贝格积分就是0。

随着这篇论文的发表，勒贝格很快收到众多学院的邀请。1902年到1903年间，他在雷恩大学任教。一年后他来到巴黎的法兰西学院。在那里他待了三年，然后接受了普瓦捷大学的职位。1910年，巴黎大学数学系任命他为首席讲师（mâitre de conferences）。法国参加一战后，勒贝格立即为国防部效力，并被指派分析确定运兵车应该以怎样的频率派往前线。战后，巴黎大学提升勒贝格为教授，他只在这个位置上待了三年，然后接受了法兰西学院的主任教授一职。在这个位置上，勒贝格度过了他其余的职业生涯。

虽然他的概念为数学分析带来了革命，勒贝格在数学界谈不上有个人影响。勒贝格对学院内外的政治都不感兴趣，他似乎满足于授课，写文章，孑然一身。虽然他的成果很了不起，但是他整个职业生涯中只监督了一篇博士论文。法国的数学界对其贡献的重要性赞许有加。勒贝格于1912年获得欧乐维格奖，1914年获彭色列奖，1917年或桑托奖，1919年获小德欧梅奖。1922年入选科学院，是他所获得的荣誉中的最高荣誉。

勒贝格的生活非常低调，以致于我们对他的家庭生活知之甚少。1903年在雷恩的时候，他和一位他高等师范学校同学的姐姐路易丝-玛格丽特·巴列结婚。他们育有一子雅各。12年婚姻后，他们于1916年离婚。勒贝格终其余生都是一个人生活，健康状况也不好。他对德国占领法国也一直不开心，生了一场病后，他死于1941年7月26日，终年66岁。