要不要乘法口诀表？

在前言中^1，我们已经讨论了特拉赫腾贝格系统((Trachtenberg system。以后在不引起歧义的情况下简称“系统”。 ))的目标。现在我们来看看方法本身。首先要说的是一种进行基本乘法的新方法：不用记忆乘法口诀来进行乘法运算。这有可能吗？这不但是可能的，而且还很容易。

不过还是要解释一句：我们不是说我们不同意用口诀表。大部分人都很了解这张表格——事实上，可以完美掌握，除了一些地方可能有疑问之外。8乘7，或者6乘9可能会让我们中很多人犹豫一下，但是小一些的数字，比如4乘5是每个人都能掌握的。^2我们赞成使用这一好不容易才获得的知识。我们现在想要做的，是将其进行汇总。本章稍后，我们会回到这一点来。现在我们希望不依靠口诀表来做乘法。

我们先来看乘以11的情形。为了解释起来方便，我们先将该方法以规则的形式加以阐述：

乘以11

• 被乘数的最后一位数字成为结果的最右一位数字。
• 被乘数的后续每一位数字与它右邻的数字相加。
• 被乘数的第一位数字成为结果的最左一位数字。而这也是最后一步。

在系统中，你每次从右向左写下答案的一个数字，就和你使用现在的系统时一样。举个简单的例子，633乘以11：\(\frac{633}{答案在这里} \times 11\)

结果会写在633之下，随着我们遵循规则，一个数字一个数字从右到左地出现。这也是我们今后进行操作的形式。在我们的例子中，被乘数上方的小点可以很快地表明在我们计算的每一步中，哪个数字正被用到。现在让我们来运用规则：

规则一：

写下633最后的一位数字，作为答案最右边的数字：^3

规则二：

633中的后续每个数字和它的右邻相加。3+3=6：\(\frac {6\dot{3}\dot{3}}{?63} \times 11\)

再次引用规则，6+3=9：\(\frac {\dot{6}\dot{3}3}{963} \times 11\)

规则三：

633的第一个数字6，成为答案最左边的数字：\(\frac {\; \dot{6}33}{6963} \times 11\)

答案就是6963。

数字再长也是用一样的处理方法。第二个规则：“被乘数的后续每一位数字与它右邻的数字相加”在上面这个例子中用了两次。如果数字更长，就会被多次使用。我们来看721324乘以11的例子：

\(\frac {721324}{答案在此书写} \times 11\)

规则一：

写下721324的最后一位数字，作为答案最右的一位数字：\(\frac {72132\dot{4}}{?????4} \times 11\)

规则二：

721324后续的每个数字与它的右邻相加。

2+4=6：\(\frac {7213\dot{2}\dot{4}}{????64} \times 11\)

3+2=5：\(\frac {721\dot{3}\dot{2}4}{???564} \times 11\)

1+3=4：\(\frac {72\dot{1}\dot{3}24}{??4564} \times 11\)

2+1=3：\(\frac {7\dot{2}\dot{1}324}{?34564} \times 11\)

7+2=9：\(\frac {\dot{7}\dot{2}1324}{934564} \times 11\)

规则三：

721324的第一个数字成为答案最左边的数字：\(\frac {\; \dot{7}21324}{7934564} \times 11\)

答案就是7934564。

如你所见，这一大数中的每个数字都用到了两次。一次是作为“数字”，然后在下一步，作为“右邻”。在上例中，被乘数中的1，在其为答数提供4这个数字时是作为“数字”，而在下一步，它为3这个答数作出贡献，成为“右邻”:

\(\frac {\;72\dot{1}\dot{3}24}{??4???} \times 11\) \(\frac {\;7\dot{2}\dot{1}324}{?3????} \times 11\)

我们可以不用三条规则。如果我们以一种自然且符合常理的方式来运用规则，就可以只用一条“加上右邻”的规则。不过我们首先需要在给出的数字前添一个0，至少想象那里有一个0。然后我们就可以对给出数字中的每个数位应用“加上右邻”这一条规则：

3没有邻居，所以什么都不用加：\(\frac {063\dot{3}}{???3} \times 11\)

然后像之前操作的那样：\(\frac {0633}{?963} \times 11\)

0+6=6：\(\frac {\dot{0}\dot{6}33}{6963} \times 11\)

这个例子展示了我们为什么需要在被乘数前加一个0。那是为了提醒我们不要太早结束计算。如果没有这个前导的0，我们可能会忘记书写最后的那个6，然后我们就可能认为答案是963。答案要比给出的数字长一位，而前导0就是为了提醒我们这一点。

请你自己做个练习：\(441362 \times 11\)。要以正确的形式书写：

0441362 X 11

如果我们从2（也是正确的开始位置）开始，然后向左开始运算，每次加上“右邻”，那一定能得到正确的答案：4854982。

有时，你在相加数字和它的右邻时，会得到两位数。比如\(5+8=13\)。此时，你要写下3，并“进位”1——这些都是你很熟悉的了。但是在本系统中，你永远没有必要进位大数字。就算有进位，也只能是1，或者是2（见以后的例子）。这让我们在处理复杂问题时，有了巨大的不同。

对进位的1，加个点就够了；对于更少见的进位2，可以加双点。

这里的\(\dot{2}\)是12，来自7+5：\(\frac {01754}{19\dot{2}94} \times 11\)

请自行做个测验：$715624\times 11`。可以这样写：

0715624 X 11

这一个大数字中，数字5要进位1。

该问题的正确答案是7871864。

在非常特殊的大数情况下，它第一位是9，然后又是一个大数字（比如8）。我们来看这样一个数字：98834。我们在最后一步可能得到10：

\(\frac {\;\;\;98834}{10\dot{8}\dot{7}\dot{1}74} \times 11\)

乘以12

任意数乘以12，可以这样做：

依次加倍一个数字并加上它的右邻。

这和乘以11一样，只有一点不同：我们先加倍“数字”再加上“右邻”。如果我们要计算413 X 12，应该这么做：

第一步：

将右边的数字加倍并写下来（它没有右邻）：\(\frac {041\dot{3}}{???6} \times 12\)

第二步：

将1加倍并加上3：\(\frac {04\dot{1}\dot{3}}{??56} \times 12\)

第三步：

将4加倍并加上1：\(\frac {0\dot{4}\dot{1}3}{?956} \times 12\)

最后一步：0加倍还是0，加上`4``：\(\frac {\dot{0}\dot{4}13}{4956} \times 12\)

答案是4956。如果你自己进行了计算，一定会发现计算非常快而且很简单。

你现在自己试一下计算\(63247\times 12\)。写下这个数字的时候，要将各位数字分开，将答案的每个数字对直写在63247中对应数字的正下方。这不光是能养成整洁的好习惯，更对防止出错有非常大的作用。特别是在本系统的乘法中，我们提及这一点是因为它能标识出“数字”和“右邻”。答案中的下一个空白，也就是答案的下一个数字要写入的地方，正好在这个“数字”的下方（本例中，你要加倍这个数字）。而右边的那个数字是“右邻”，要被加上。本例可以如此计算：

加倍7得14，进位1：\(\frac {06324\dot{7}}{?????\dot{4}} \times 12\)

加倍4得8，加7，加1，得16，进位1：\(\frac {0632\dot{4}\dot{7}}{????\dot{6}\dot{4}} \times 12\)

加倍2得4,加4，加1，得9：\(\frac {063\dot{2}\dot{4}7}{???9\dot{6}\dot{4}} \times 12\)

最后会得到：

\(\frac {063247}{7\dot{5}89\dot{6}\dot{4}} \times 12\)

乘以5，乘以6，乘以7

所有这些乘法（乘以5，6，7）都会用到对一个数字“取半”。我们将“取半”放在引号中是因为那是简化了的一半。我们取半时用了简易方法，扔掉了所有分数部分（如果有的话）。将5“取半”得2。那实际上是\(2\frac{1}{2}\)，但我们不会用到分数部分。所以，3“取半”是1，1“取半”是0。当然了，4“取半”是2，所有的偶数都是如此。

这一步应该瞬时完成。我们不要对自己喃喃自语“4的一半是2”或者其他类似的言语。我们看到4就说出2。试着用下面这些数字来做一下：

2, 6, 4, 5, 8, 7, 2, 9, 4, 3, 0, 7, 6, 8, 5, 9, 3, 6, 1

奇数（1, 3, 5, 7, 9）的特殊性在于“丢掉”分数部分。偶数（0, 2, 4, 6, 8）总会给出常规的结果。

乘以6

现在让我们在试试“取半”的把戏。乘以6的第一部分规则是：

每个数字加上它右邻的“取半”。

我们先假定，这就是乘以6需要知道的所有规则。然后来解决这个问题：

\(0622084 \times 6\)

第一步：4是这一长串数字的第一个“数字”，它没有“右邻”，所以不用加什么：

\(\frac{062208\dot{4}}{??????4} \times 6\)

第二步：第二个数字是8，它的右邻是4，所以我们取出8，加上4的“取半”（2），得到了10：

\(\frac{06220\dot{8}\dot{4}}{?????\dot{0}4} \times 6\)

第三步：下一个数字是0，我们将其加上它右邻8的“取半”4，得到4，然后加上进位来的1：

\(\frac{0622\dot{0}\dot{8}4}{????5\dot{0}4} \times 6\)

对剩下的数字（2, 2, 6和想象中的0）依次重复上述过程：

\(\frac{0622084}{37325\dot{0}4} \times 6\)

你要不要试试？看看有多简单？试着计算下面两个乘法：

\(04404 \times 6\)

\(028688424 \times 6\)

第一个的答案是26424，第二个的答案是172130544。

我们所进行的运算对这些问题都给出了正确答案。但是，乘以6的完整规则还有待补充。完整的规则是：

每个数字加上它右邻的“取半”；如果数字是奇数，则再加5

“如果是奇数”的意思是“数字”是奇数，和“右邻”是不是奇数没有关系。我们看这个“数字”，看它是奇数还是偶数。如果是偶数，那我们只要将它加上右邻的一半；如果是奇数，我们要将它加上5，再加上及右邻的一半（和刚才的做法一样）。比如：

\(0443052 \times 6\)

数字3和5是奇数。我们看到被乘数后就能发现这一点。我们开始处理3和5的时候，因为这两个数都是奇数，我们应该额外多加5。计算过程如下：

第一步：2是偶数也没有右邻，所以照抄下来：

\(\frac{044305\dot{2}}{\;??????2} \times 6\)

第二步：5是奇数！5加5，加上2的“一半”，得到11：

\(\frac{04430\dot{5}\dot{2}}{?????\dot{1}2} \times 6\)

第三步：5的一半是2，再加上进位：

\(\frac{0443\dot{0}\dot{5}2}{????3\dot{1}2} \times 6\)

第四步：3是奇数！3加5是8：

\(\frac{044\dot{3}\dot{0}52}{???83\dot{1}2} \times 6\)

第五步：4加上3的一半：

\(\frac{04\dot{4}\dot{3}052}{??583\dot{1}2} \times 6\)

第六步：4加上4的一半：

\(\frac{0\dot{4}\dot{4}3052}{?6583\dot{1}2} \times 6\)

最后一步：0加上4的一半：

\(\frac{\dot{0}\dot{4}43052}{26583\dot{1}2} \times 6\)

答案是2658212。当然，所有这些解释只是为了在我们第一次展示方法时做到尽可能的清晰明了。在实际应用中，因为加上右邻一半的步骤非常简单，所以整个过程进行得非常快。重要进行适当程度的联系，就会成为“自动”过程，而不是意识中的计算。

如果你自行进行如下两个运算，也许会更清楚地看到这点：

\(08234\times 6\)

\(06250188\times 6\)

第一式的答案是49404，第二式的答案是37501128。

我们用来乘以6的都是很长的数字。如果我们试图乘以一位数（比如8 X 6），这个方法还适用吗？当然还适用，而且事实上不用做任何修改。试试用相同的步骤来计算8X6：

8没有右邻，8加上右邻的一半还是8：

\(\frac{08}{?8} \times 6\)

0加上8的一半是4：

\(\frac{08}{48} \times 6\)

如果被乘数是奇数（比如是7），我们在第一步就要加上5。当然，我们不用在第二步加5，因为0被认为是一个偶数：

7加上5，加上什么都没有的“一半”：

\(\frac{07}{?\dot{2}} \times 6\)

0加上7的一半，再加上进位的1：

\(\frac{07}{4\dot{2}} \times 6\)

也许大多数人会觉得他们心中记得住6的乘法口诀。也许超过一半的非数学人员对它有信心——尽管这样的信心毫无来由。我们这里的要点不在这里。这个乘法方法中用到的技术在稍后更为复杂的情形中还会被使用，因此它们脱离任何记忆中的口诀表而需要存在。引入这些新步骤最好的方式是将其应用在相对熟悉的方面。这也是我们现在所做的。

另外——这一点比看上去更加重要——这也是开始培养正确的心算习惯的方式。我们都听到过对一般人阅读习惯的批评，也听过开发快速阅读能力的方法。批评中提到太多人有一个字母一个字母阅读，拼写出他们读到的东西的习惯，或者至少大部分情况下如此。我们被要求养成阅读习惯，每次识别一个单词或一个词组。其他要点也被提及。它们都会归结到一点：大部分人阅读糟糕，到了养成无效阅读习惯的程度。

算术中，同样的一般原则也是适用的。某人在进行算术的时候有着一些坏习惯，结果就是他浪费了一些时间和精力。只有将他们大部分的时间用在处理数字上的那些人（比如会计），才会最终给自己找到正确的步骤。而我们其他人，尽管可能不会将计算作为我们的生计，只要通过些许努力和时间也能学到这些方法。这些资料中有一些在本章和下章中得以标出。

这些思维步骤中的一个，也是很简单的一个，已经被提及了——就是我们提到对“右邻”进行“取半”的时候。我们通过看一个个位数（比如2或者8）立即说出是1或者4，而不要经过任何思维步骤而进行了一些练习。我们一看到2或者8，答案应该立刻出现在我们的脑海中，就像是反射作用那样。读者回头拿我们给出的那些供练习的数字再做一次，应该能做得很好。

另外一个正确的思维步骤是只对我们说出加上右邻或者右邻一半的结果。比如这样：

\(\frac{02\dot{6}\dot{4}}{??84} \times 6\)

8是6加上4的一半。而不是说：“4的一半是2，而6加2等于8”。反之，看着6和4，看到4的一半是2，然后对自己说“6, 8”。一开始这会比较难，所以也许更好的做法是对自己说：“6, 2, 8”。

另外一个需要锻炼的地方是这一步：如果数字（不是右邻）是奇数要加5。比如这个例子：

\(\frac{06\dot{3}\dot{4}}{??\dot{0}4} \times 6\)

0是10的个位0，我们已经标记了。而10是3加上5（因为3是奇数）加上2（4的一半）。一开始，正确的步骤是说“5, 8, 2, 10”。经过一段时间练习后，应该最终被约简为“8, 10”。因为3是奇数而要加的5应该先被加，否则我们可能会忘记的。

同样的，如果有标记进位1的小点，也应该在加右邻（乘以11）或者右邻一半（乘以6）之前先加。如果等到加了右邻后再处理进位1，有时会忘记这么做的。在上例中，答案的下一位是类似这样得出的：

\(\frac{0\dot{6}\dot{3}4}{?8\dot{0}4} \times 6\)

我们看着6，说出7（加上进位1），然后我们说8（加上3的一半）。一开始，更好的方法是，看着6，（加上进位）说出7，然后说3的一半1，然后说出8。最后写下8。

如果又有进位，又要加5（因为数字是奇数），那么说出6而不是说出5，然后加上数字本身。这样可以少一步，而且也很容易习惯。

请拿出纸和笔，试着只用正确的思维步骤来计算下面这些习题（答案在后面）：

乘以11（加右邻）：

04232 047492

乘以12（加倍再加右邻）：

04232 047492

乘以6（如果奇数就加5，再加右邻）：

02222 02004 04232 04748 02906 05244 03865 04111

答案为：（略）

乘以7

乘以7的规则和乘以6的规则非常相似：

数字加倍，加上右邻的取半；如果数字为奇数，再加5。

假定我们要计算4242 X 7。4242中没有奇数，所以我们不需要额外加5。在本例中，过程和乘以6类似，只是我们现在要加倍：

第一步：加倍数字2：

\(\frac {0424\dot{2}}{????4} \times 7\)

第二步：加倍4再加上右邻的一半：

\(\frac {042\dot{4}\dot{2}}{???94} \times 7\)

第三步：加倍2再加上右邻的一半：

\(\frac {04\dot{2}\dot{4}2}{??694} \times 7\)

第四步：

\(\frac {0\dot{4}\dot{2}42}{?9694} \times 7\)

最后一步：0加倍还是0，但要加上右邻的一半：

\(\frac {\dot{0}\dot{4}242}{29694} \times 7\)

下面这个例子中包含奇数。3和1都是奇数：

第一步：2加倍，没有右邻：

\(\frac {0341\dot{2}}{????4} \times 7\)

第二步：1加倍，加上5（因为1是奇数）得7，加上2的一半：

\(\frac {034\dot{1}\dot{2}}{???84} \times 7\)

*第三步：4不是奇数，加倍再加1的一半：

\(\frac {03\dot{4}\dot{1}2}{??884} \times 7\)

第四步：

\(\frac {0\dot{3}\dot{4}12}{?\dot{3}884} \times 7\)

**最后一步：0加倍还是0，但要加上3的一半和进位1：

\(\frac {\dot{0}\dot{3}412}{2\dot{3}884} \times 7\)

在脑中，正确的步骤应该是：

• 如果有进位1，那么看到点要说“1”。
• 看看下一个要处理的数字，注意它是否为奇数。如果是，在进位1上加5，说“6”；如果没有进位，就说“5”。
• 看这个数字，在脑子中将其加倍，说出5和这个加倍后数字的和。比如说，这个数字是3，我们说“5”，然后说“11”。这是因为3加倍得到6再加上5可以在一步内完成。
• 看右邻（比如说是6），我们在已经有的数字上再加它的一半。我们刚说了，我们现在得到的是11。如果右邻是6，我们接着说“14”。

让我们一次一小步地来处理这个流程。做这些练习的思维训练非常有价值，因为它能培养集中度，而集中度基本上就是成功的秘诀。但是，不能一蹴而就，我们可以帮助自己采用下面几个独立的阶段。

首先，观察下列数字并立即说出这个数的两倍（不要经过任何中间步骤）。看到3，立即说出6而根本不说出3：

2, 4, 1, 6, 0, 3, 5, 1, 4, 3, 8, 2, 6, 3, 7, 5, 9, 2, 1, 0, 6, 3, 5, 2, 6, 8, 7, 4

第二步，在下面每一对数字中，看左边的数字，高声说出它的倍数（看到3说出6），然后加上它的右邻（比如对于“3 4”这一对数，说出“6 10”）。这是计算乘以12最快的方法：

数字对	数字对	数字对	数字对	数字对	数字对
2 1	3 4	2 0	1 1	2 2	0 2
2 7	1 5	6 0	7 1	4 5	0 9
3 2	3 8	7 4	5 2	8 2	4 1

第三步，在下面每一对数字中，看左边的数字，高声说出它的倍数，然后加上右邻的一半（比如对于“2 6”，说出“4 7”。这是偶数乘以7的做法）：

数字对	数字对	数字对	数字对	数字对	数字对
2 6	2 7	4 0	6 1	2 6	4 4
0 4	2 2	2 9	8 1	8 8	8 9
6 6	4 3	6 7	4 9	8 1	0 7

第四步，在下面每个数字中，看到数字就说“5”，然后说出5加上该数字加倍（比如看到3，就说“5，11”）：

7, 5, 3, 1, 9, 3, 7, 5, 1

//然后再从头做一次！//

第五步，在下面每一对数字中，看左边的数字，说出“5”，然后说出5加上这个数字的加倍（就是我们刚做的），然后立刻加上右邻的一半，并说出加上这个一半后的结果（比如对于“3 4”，说出“5 11 13”）。这是奇数乘以7的做法：

数字对	数字对	数字对	数字对
1 0	1 2	1 6	1 8
3 0	3 2	3 8	3 4
5 0	5 6	7 0	7 2

现在来看看你能多快地计算乘以7。先试试这些偶数，因此不需要加5，只要加倍数字再加上右邻的一半：

• 0202
• 0222
• 0602
• 0444
• 0642
• 0846

然后我们用一些包含奇数位的数字来收尾（这时要加5）：

• 0223
• 0302
• 0254
• 0274
• 0618
• 0134

乘以5

乘以5的规则和乘以6、乘以7的规则类似，但更简单。不用加“数字”（乘以6）也不用加倍数字（乘以7），我们只用到该“数字”。我们看这个数字，判断它的奇偶。如果是奇数，就和以前一样加5：

右邻取半，如果是奇数则再加5。

假定我们要计算426 X 5：

看到6，为偶数，不用加5，也没有右邻： \(\frac {042\dot{6}}{???0} \times 5\)

看到2，为偶数，取6的一半： \(\frac {04\dot{2}\dot{6}}{??30} \times 5\)

看到4，为偶数，取2的一半： \(\frac {0\dot{4}\dot{2}6}{?130} \times 5\)

看到0，为偶数，取4的一半： \(\frac {\dot{0}\dot{4}26}{2130} \times 5\)

如果被乘数中有奇数位，我们要加5。

同前： \(\frac {043\dot{6}}{???0} \times 5\)

3是奇数，说出5加3： \(\frac {04\dot{3}\dot{6}}{??80} \times 5\)

最后： \(\frac {0436}{2180} \times 5\)

这很简单。这里很少涉及数字。但是一开始看会非常奇怪，因为你必须要做的有点绕脑子：你用的是右邻而不是你要计算答案的那位上的数字。事实上，各就各位是良好的做法。稍后在进行两个多位数相乘的计算时，我们会发现需要略微留意一下，记住我们在要进行乘法的数字中的位置。这个乘以5的方法是一些初步的练习。

试试如下乘以5的计算：

• 0444
• 0428
• 0424882
• 0434
• 0647
• 0256413
• 0142847

（答案略）

乘以8和乘以9

要乘以8和乘以9，需要一个新的思路步骤，也就需要进一步的思维训练。这个新步骤牵涉到将“数字”与9或者10相减。假定我们要计算4567乘以8或者乘以9。在这两种情况下，第一步是将被乘数最右一位的数字（7）与10相减。我们开始做的时候，看到4567最右边的数字，说出“3”。我们不要经过说出“10减7为3”的步骤。这应该是一个瞬时反应。我们看到7然后说出“3”。看看你的反应有多快：看看下列每个数字，然后立即说出它与10相减后的结果：

7, 6, 9, 2, 8, 1, 7, 4, 2, 3, 9, 6, 5, 3, 1, 9

现在你可以轻松快速地进行乘以9的计算而不需要使用乘法口诀表。要使大家清楚，最好的方法是表述规则，但不用你去记忆——因为经过一些训练，它会在你的脑海中生根。规则是这样的：

乘以9

• 被乘数最右一位与10相减。这将是答案的最右一位数字。
• 依次一个数字一个数字开始，将其与9相减，并加上右邻。
• 最后一步，来到被乘数前导0的位置，右邻减1并作为答案的最左的数字。

当然了，在所有这些步骤中，需要知道的是：如果有进位1，需要和平时一样加起来。

下面是一个演示，表明8769*9是怎么计算的：

\(\frac {08769}{789\dot{2}1} \times 9\)

第一步：将8769的9与10相减，，于是得到答案中的1。

第二步：将6与9相减（得到3）并加上右邻9。得到12，于是记下进位和2。

第三步：7与9相减是2，加上右邻6得到8，加上进位得到9。

第四步：8与9相减是1，加上右邻得到8。

第五步：这是最后一步。我们来到最左边的0位。于是将8769最左边的数字减去1，而7就是答案最左边的数字。

请自己试试：8888乘以9

\(08888 \times 9\)

答案的最后一位是2，因为8与10相减是2。该计算中没有进位，最左边的数字是7，也就是最后一个8减去1。正确答案是79992。

下面有一些练习。一开始的比较简单，然后稍微难一些。

• 033
• 098654
• 086733
• 0626
• 0805
• 07754965

乘以8

• 第一位：与10相减并加倍。
• 中间的数字：与9相减并加倍，加上右邻。
• 最左一位：被乘数最左一位减去2。

乘以8和乘以9是一样的，但是要加倍，最后一步要从被乘数最左一位减去2而不是减去1。其计算如下：

\(\frac {078\dot{9}}{???2} \times 8\)

这个2来自9与10相减然后加倍。789中的8是属于“中间的数字”，于是将8与9相减，加倍，再加上右邻：

\(\frac {07\dot{8}\dot{9}}{??\dot{1}2} \times 8\)

7也是“中间数字”。我们要做到789前面的那个0的时候才是到了最左一位。于是对于7，我们要对2（7和9相减是2）加倍，得到4，再加上右邻8：

\(\frac {0\dot{7}\dot{8}9}{?\dot{3}\dot{1}2} \times 8\)

最后，左边的7减去2得到而得到5，当然要再加上进位的1：

\(\frac {\dot{0}\dot{7}89}{6\dot{3}\dot{1}2} \times 8\)

请注意，相比传统的乘法，这确实更加简单更加容易——只要熟悉这个方法。通过传统方法，我们必须不光要熟悉乘法表（而很多人对我们这里需要的8乘以7，8乘以8和8乘以9不是很有把握），我们必须进7，再进7，增加了犯错的可能。反之，不用乘法表格的方式只需要进位1。

当然，除非使用这个方法时不用考虑任何“规则”，那么就还没有掌握这个方法。只要略加练习，就足以自动完成这个步骤。半个小时或者一个小时的练习，与学校里的孩子花费很多很多小时专门进行乘法口诀表练习相比，确实不算什么。

试试如下的练习，将每个数字乘以8：

• 073
• 049
• 069
• 098
• 07777
• 08586
• 06288
• 03669

即使做一位数乘法，同样的步骤也能工作得很好。假定我们要乘以9（不用加倍）而要被乘的数字是7。没有中间数字，于是我们从10中减去7作为我们通常的第一步，然后将7减去1作为我们常规的最后一步。看起来像这样：

\(\frac {07}{63} \times 9\)

这些个位数形成一个简单的模式，如下：

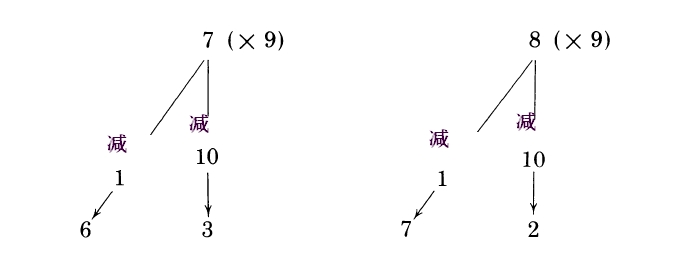
在考虑乘以8的时候，与此类似，只是变成“从10减并加倍”和“减2”：

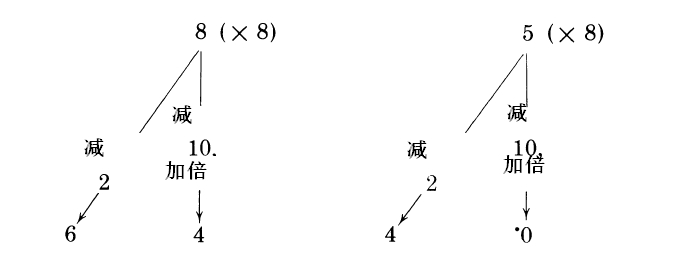
乘以8的时候，如果乘的数字比较小（1到5），我们可能需要进1。但通常这没有必要，因为我们都知道小数字的乘法表。人们只是对比较大的数字（7乘以8）才可能有点小问题。对这些数字来说，8的计算不用进位。对9来说，永远不需要进位。

（略过说明）

乘以4

• 从10中减去右手第一位的数字，如果是奇数则加5。
• 从9中减去其它各位数字，如果是奇数，加上右邻的一半。
• 在给出数字的前导0下，写下右邻数字一半并减1。

例子1：20684乘以4

第一步：将20684中的4与10相减：

\(\frac {02068\dot{4}}{?????6} \times 4\)

第二步：8与9相减，加上4的一半得3：

\(\frac {0206\dot{8}\dot{4}}{????36} \times 4\)

第三步：6与9相减，加上8的一半得7：

\(\frac {020\dot{6}\dot{8}4}{???736} \times 4\)

第四步：0与9相减，加上6的一半得2：

\(\frac {02\dot{0}\dot{6}84}{??\dot{2}736} \times 4\)

第五步：2与9相减，加上0一半及进位得8：

\(\frac {0\dot{2}\dot{0}684}{?8\dot{2}736} \times 4\)

最后一步：2的一半减去1得0：

\(\frac {\dot{0}\dot{2}0684}{08\dot{2}736} \times 4\)

例子二：例子一中我们不用“加5”，因为20684的各位数字都是偶数。下面一个例子中的数字有一些位是奇数。365187乘以4：

第一步：10减7是3，再加5（因为7是奇数）得8：

\(\frac {036518\dot{7}}{??????8} \times 4\)

第二步：9减8是1，加上7的一半得4：

\(\frac {03651\dot{8}\dot{7}}{?????48} \times 4\)

第三步：9减1是8，加上5加上8的一半得7：

\(\frac {0365\dot{1}\dot{8}7}{????\dot{7}48} \times 4\)

第四、第五、第六步：我们重复以前的步骤。要记得3和5是奇数，所以需要加5：

\(\frac {0365187}{?\dot{4}6\dot{0}\dot{7}48} \times 4\)

最后一步：3的一半是1，减1加进位1得1：

\(\frac {0365187}{1\dot{4}6\dot{0}\dot{7}48} \times 4\)

作为必要的练习，我们进行如下计算：

• 02688
• 0247847
• 0860442
• 054618

乘以其他数字

3

乘以3和乘以8类似，但有几个特别之处。乘以8的时候，我们是加上右邻，但乘以3时是加上右邻的一半。当然，如果该数字是奇数，也要再加5。我们来看看2588乘以3：

第一个数字：从10中减去这个数字并加倍。如果这个数字是奇数那么加5。

中间的数字：从9中减去各位数字并加倍，加上右邻的一半。如果数字是奇数，那么加5。

最左边的数字：该数字取半，然后减去2。

第一步：10减去8再加倍，没有右邻，又是偶数：

\(\frac{0258\dot{8}}{????4} \times 3\)

第二步：9减去8再加倍，加上右邻8的一半：

\(\frac{025\dot{8}\dot{8}}{???64} \times 3\)

第三步：9减5再加倍，加上右邻8的一半，再加5：

\(\frac{02\dot{5}\dot{8}8}{??\dot{7}64} \times 3\)

第四步：9减2加倍，加上右邻5的一半：

\(\frac{0\dot{2}\dot{5}88}{?\dot{7}\dot{7}64} \times 3\)

最后一步：2的一半加上进位1，减去2：

\(\frac{\dot{0}\dot{2}588}{0\dot{7}\dot{7}64} \times 3\)

乘以2

乘以2很简单。我们只要每一位乘以2，记住进位，不用考虑右邻。

乘以1

乘以1不会改变数字。

这最后几个乘以小数字的规则之所以出现在这里，是为了保持完整性。

注意，所有情形下，运算只要牵涉几个数字，而且都很简单。