罗巴切夫斯基(Nikolai Ivanovich Lobachevsky,1792-1856)——生平与成就

福尔摩斯故事《四签名》中,柯南道尔让这位大侦探做出了如下声明:
排除所有不可能后,剩下的——不管它如何地不可能——就必然是事实。
19世纪初的几何学就是如此。花费了两个世纪试图证明欧几里德的平行公设而无果后,是时候让几何学家来证明其不可证,而且别种类型的几何是可能的——不管它有多么不可能。两位数学家:来自俄罗斯的罗巴切夫斯基和来自匈牙利的鲍耶几乎同时做出了这一成就。他们的生平与成就在本章和下一章中分别讲述。
罗巴切夫斯基于1792年12月1日生于马卡利夫镇,距离下诺夫哥罗德市(坐落于贯穿俄罗斯心脏的伏尔加河之上)以北40英里。他是三兄弟中的老二。他的父母是亿万·马克西莫维奇和普拉斯科娃·亚历山大洛夫娜,几年前从波兰移民而来。对罗巴的父亲,我们知之甚少,只知道他是政府土地测绘部门的官员,收入不多,勉强能维持家用。罗巴七岁的时候,他父亲去世了。新寡的普拉斯科娃搬家到喀山市以东200英里的地方,差不多已经在西伯利亚边境,希望能靠教小孩子谋生。罗巴终其余生都将在这个新家乡度过。
普拉斯科娃的三个儿子是她的第一批学生,而且是好学生。每人都获得了政府奖学金以支付他们进入喀山一所当地学校的费用。罗巴于1802年入学,五年后以最高荣誉毕业,并获得政府奖学金进入当地大学。喀山大学于1805年才开始招生,是沙皇亚历山大一世早年统治期间所进行的众多教育改革成果之一。
大学是如此的新,又是如此的远,意味着它没有一个固定的师资队伍。于是它从整个东欧和中欧招聘其年轻的教师团队。确实,在罗巴就学期间,喀山大学能自夸说有着最好的学者,比所有大学——除了几所最好的德国大学之外——所拥有的都好。这些年轻学者带来了数学、物理、天文、哲学、教育学方面最新的理念。
这些学者中对罗巴最重要的是巴特尔斯(1769-1833)。他刚刚在德国谋到了在一所学校中教授数学的职位。不过他很幸运,因为伟大的高斯是他的学生之一。他们多年以来一直保持着通信联络。
巴特尔斯的讲课很快说服罗巴放弃了学习医药的计划。巴特尔斯教授了欧拉对微分和积分的处理,拉格朗日的分析力学,高斯的《算术论辩》,蒙热关于几何中数学分析的应用的工作,以及蒙托克莱四卷本的数学史。蒙托克莱详细的讲述了试图证明欧几里德平行公设的历史,这可能就是罗巴对该问题感兴趣的原因。
从多方面看,罗巴都没有表现初作为学生应有的模范行为。时不时地,大学行政官员会批评他“顽固”、“过于自我为中心”,还有无神论倾向。1811年8月,喀山地区学监向校董会建议,后者应该向罗巴这位“坏行为的典型”表明“我们对其不得体的行为深感遗憾。他的超凡能力会被此等行为笼罩上乌云。”幸运的是,巴特尔斯和其它教授对罗巴的了解要比那些官员们深得多。他们建议出于其“在数学和物理方面非凡的才能”,而授予他硕士学位。那年末,他获得了该学位。
那年头,在喀山要找到一个教书的工作很不容易。罗巴一定觉得是运气到了家,因为他的哥哥阿历克谢请了病假,不能为那些需要一个大学文凭以谋求提升的那些政府雇员们教授初等数学。大学里的权威们一定是被这位以前的刺儿头的教书能力打动了。1814年,他们提升他为讲师,两年后又擢升他为副教授,1822年又成为教授。整个在校教书期间,罗巴除了教授数学,也教授物理和天文学。但是,他最喜欢的永远是教授平面和立体三角学。
罗巴讲课时用的是自己的笔记,希望有朝一日能成为教科书出版并有些额外的收入。这些笔记的手稿表明,直到19世纪20年代初,罗巴和他之前的很多人一样,都试图证明欧几里德的平行公设。手稿中包括证明该公设的三个尝试,但在笔记的其他地方,罗巴承认没有一个是确定性的。
我们不知道是什么原因促使罗巴放弃证明平行公设的努力。他的同事巴特尔斯可能向他传递了来自高斯的一些提示。或者,他也可能受到哲学家卢布金的启发。后者1812年来到喀山任教,传授的是严格的经验主义,而反对康德认为空间是合成的、先验的范畴,并组成了我们的经验。他认为空间是从其中得出的体验。罗巴后来写道:
自从欧几里德以来这差不多2000年,种种尝试均告无果。这让我怀疑真理——而真理是值得被证明的——不包含在这些数据本身之中。要证明之,需要实验的帮助,需要天文的观察,这正是自然法则。
以下是罗巴1840年的论文《平行理论的几何研究》的简要回顾。这也是他最成熟的作品,本书也有选入。
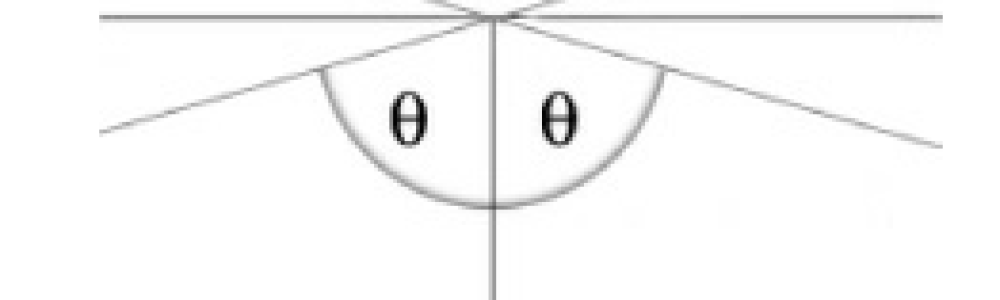
他一开始先考虑一个点P,一条直线l和P在一个平面但不包含P。然后他考虑经过P而垂直于垂线PB的线。在欧式几何中,这是唯一一条经过P而不与直线l相交的直线,而这也是罗巴在构建非欧几何中要放弃的假设。他假定还有别的经过P的线而不与l相交。这些不相交的直线与那些经过P但和直线l相交的直线,由两条线x和y(如下图所示)分开。直线x和y也不和直线l相交。罗巴将这些线定义为直线l的平行线。每条线都有一个确定的平行方向:x向右平行,而y向左平行。
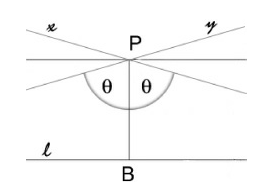
角度θ是垂线PB和这两条平行线所成的角度,被称为线段PB的平行角。常规欧式几何中,θ = 90°。而罗氏几何中,θ是P到B的距离的函数。如果距离无限大,那么该角度趋向于0°,如果距离无限小,则趋向90°。
做出这一替换公设后,罗巴继续证明了,在这另一种几何中:
- 给定直线l1上的一点,如果l1平行于l2,那么对于l1上的每一点,l1都平行于l2。(这一特性被称为“持续性”)。
- 如果l1平行于l2,那么l2平行于l1。(反射性)
- 如果l1平行于l0,而l2也在同一方向平行于l0,那么l1平行于l2。(传递性)
到目前为止,这些结论都还算中规中矩。每个结论在欧式几何中都能找到直接的对应。但是下一个结论就怪异了,找不到欧式几何中的对应。
- 如果l1平行于l2,那么l1渐近于l2,也就是说,l1和l2可以互相无限的靠近。
欧式几何中正相反,两条平行线之间互相保持相同的距离。
罗巴在1823年的手稿中完成了他对非欧几何处理的第一波。手稿的标题是《几何》,但这一手稿直到1909年才得以发表。在手稿中,罗巴经常使用的一个词儿是“虚几何”来描述他发明的新几何。手稿明确表明,他将欧式几何认为是这一更广义的“虚几何”的一个特例,就像实数是虚数(复数)的一个特例一样。
不知出于什么原因,罗巴在两年的时间里选择不发表他的结果,直到1826年2月,他向其喀山的同事宣读了一篇论文(该篇论文已经散佚),标题为《几何基础的简明纲要》。受到同事们接受程度的鼓励,罗巴将他的成果汇编于他的系列讲座《几何原理》,并在1829-1830学年的《喀山通讯》上分批发表。
19世纪第一个25年见证了俄罗斯数学家做出的第一个重要贡献。受到俄罗斯宫廷法兰西风尚的影响,大部分位于圣彼得堡和莫斯科数学家们用法语发表文章,少数会用德语发表。而远在喀山的罗巴切夫斯基并不这么看。他将《几何原理》提交给圣彼得堡科学院,以期发表在他们发行的某个期刊中。审稿人是奥斯特罗格拉茨基,他坚决支持这样的观点,即复杂的数学论证就是无法用俄语来表述。他认为这一成果根本不值得学院加以发表。
但是在圣彼得堡的某些人——很可能就是奥斯特罗格拉茨基,还是注意到了罗巴切夫斯基。论文被拒后不久,圣彼得堡的期刊《祖国之子》发表了一篇严厉地、未署名地针对《几何原理》的评论。该评论严厉批评了罗巴切夫斯基,认为他没有足够努力地去清楚地表达他的观点。从那些认为俄语太原始而不能用于数学的人那里发出如此的批评当然一点也不奇怪。
要是喀山大学还能留住它那些伟大的教员们的话,罗巴也许还能期望他的成果能得到更好的第一反应,因为他们非常可能是支持罗巴的。不幸的是,在新沙皇尼古拉一世的统治下,1826年大学被迫解聘了众多外国教员,特别是其中就包括巴特尔斯。罗巴重写了他的工作,题为《几何新原理》之后,他选择不与圣彼得堡的学院进行交流,而只是在1835年到1838年期间发表在《喀山大学科学期刊》上。
罗巴绕开圣彼得堡的学院,同时提交了一篇以法文写成题为《虚几何》的短论文给《纯数学及应用数学期刊》,简述了他的成果。这个期刊由位于柏林的克雷勒发行,自1826年创刊以来,很快确立了其欧洲领先数学期刊的地位。这篇论文无疑读者甚众,但只有伟大的高斯留了意。天文学家斯特鲁维说,他于1834年拜访了高斯,他发现这位伟人正在读罗巴的某篇论文,而且以俄文原文阅读。要知道高斯直到六十多岁后才熟练掌握了俄语。也许是出于高斯的建议,罗巴在1840年发表了他论文的德文版本,论文题目是《平行理论的几何研究》。
除了几何方面的伟大成果,罗巴也为他的大学做了了不起的工作。1825年他被委任负责图书馆,1827年成为校长。他一共当了19年的校长。在这一职位上,他监督实施了大学在科学教育上的扩展——建了新楼,设了新课程。1828年,他发表了关于科学在教育中之角色的著名演说。受到18世纪启蒙运动精神的激励,他指出教育——而不是占据俄罗斯多数的贵族血统——应该是俄罗斯社会走向“荣光”的主要道路。
罗巴对大学的关注通常以出人意料的方式展现。1830年,喀山爆发了传染性霍乱。罗巴邀请教员,学生和他们的家人搬来大学校园。他关起校门,只对医生开放,并实施了严格的卫生条例。这有助于挽救了大学社区中大批人的生命。1842年,城市起了一场灾难性的大火,毁坏了半座城。大学很多建筑被毁,包括新近完工的图书馆。幸运的是,罗巴有着清晰的头脑,抢救了图书馆里的设备和书籍。两年后,多亏他的努力,它们有了新家。
1837年,沙皇尼古拉一世擢升罗巴为波维尔——一名世袭贵族成员,用以表彰他在高等教育方面做出的众多贡献。这一荣耀不到十年后就几乎就不被人铭记了。1846年,他患上了动脉硬化,因为新来的当地长官贸然剥夺了罗巴的教授资格和校长资格,认为他人老了又有病。此时罗巴才53岁。他退休回到自己的产业,过起了家庭生活。
罗巴直到快40岁才结婚。1832年,他与莫赛耶娃女士成婚。她年龄比他小很多,来自喀山当地一个富足家庭。他们一共有七个孩子。大儿子成为罗巴的骄傲和幸福。不幸的是,大儿子在他父亲“被退休”后不久死去,让罗巴陷入深深的悲哀。不久,罗巴的病情加重,还失去了视力。他于1856年2月24日去世。
罗巴切夫斯基死了,他只对为数不多的几个同时代人产生了显著的影响。高斯是其中之一,罗巴确实影响到了高斯。1842年,高斯说服哥廷根的皇家科学院授予罗巴切夫斯基通信会员的资格。几乎与此同时,他也成为莫斯科大学的名誉教授。
在喀山之外对罗巴的认同要等到他去世之后。首先是法国数学家于埃尔在1865年发表了《平行理论》的法文版。三年后,意大利数学家贝尔特拉米证明罗氏几何可以作为欧式空间中一个伪球体的表面而实现。
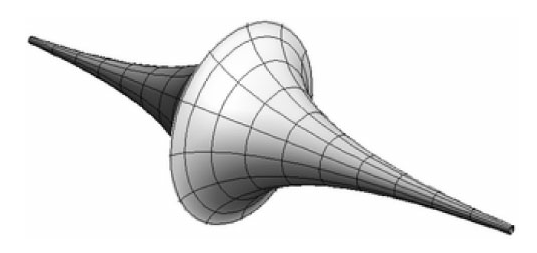
贝尔特拉米证明,在罗氏几何中,三角形内角之和小于两个直角。更重要的是,贝尔特拉米的方法证明了,违背罗氏几何将意味着违背欧式几何。
在1870年,著名的德国数学家魏尔斯特拉斯在久负盛名的柏林大学进行了罗氏几何的讲座。几年后,英国几何学家克利福德将罗巴切夫斯基比拟为“几何学界的哥白尼”。还有什么比这更贴切的赞誉呢?