本页面已浏览459次

柯西（Augustin-Louis Cauchy，1789-1857）——生平与成就

欧几里德的收入来自教学。他的学生中包括埃及国王托勒密一世。托勒密王有一次问他的老师，几何知识中是否有捷径，欧几里德的回答是：“陛下，几何之路上没有皇家大道。”也许，一般而言的数学——尤其是几何学——道路上真的是没有皇家大道。但是，要说有哪位数学家和皇室有着关联，那就是柯西。

奥古斯丁-路易·柯西生于1789年8月21日，那正是法国大革命刚萌芽的时候。他的父亲是路易·弗朗索瓦·柯西，母亲是玛丽-玛德琳·柯西（娘家姓德赛斯特），他们以他出生的月份和他父亲的名字为他起名。老柯西于1760年生于鲁昂的金属匠家里，而他母亲于1767年生于巴黎的一个官员家庭。他们于1787年成婚。

老柯西受过律师的培训，并在皇朝中担任巴黎警察局局长。随着巴士底狱的攻陷，他丢掉了这份工作而不得不在慈善局供职而继续谋生。1792年，随着恐怖统治在巴黎的降临，老柯西担心他与皇室的联系可能会让他丢了脑袋，于是他和家人一起逃到位于阿尔克伊的乡间住宅，而此时他们已经有了第二个儿子。对柯西而言，这是他逃离政治风暴之行中的第一次。

柯西在阿尔克伊的避难也许在当时看来是极为困难的，但“塞翁失马，焉知非福”？最大的好处可能就是，他们在阿尔克伊的邻居中包括伟大的数学家拉普拉斯和拉格朗日。据说后者遇见到这个小男孩的科学天赋，并警告他的父亲在他17岁之前一定不要让他看数学课本。也许是由于他自己在经典方面的教育，也许是受到拉格朗日警告的影响，老柯西利用他在阿尔克伊充足的闲暇时光开始他大儿子的教育，并为柯西打下坚实的希腊语和拉丁文的基础。后来，罗伯斯比尔倒了台，恐怖统治结束，一家人于1794年7月终于能重新回到巴黎，而老柯西也继续着他对柯西的教育。

随着拿破仑于1800年1月1日成为第一执政官，老柯西的运气也随之而来。他当选为新成立的参议院的秘书长，参议院里还有拉普拉斯和拉格朗日。在拉格朗日的建议下，老柯西让他儿子在13周岁生日后不久进入巴黎的万神殿中央理工学院学习。年轻的柯西在学院花了两年时间学习古代语言，绘画和自然历史。他对古代语言非常精通，赢得了拉丁作文以及希腊诗的一等奖。虽说他在学习古代语言方面展示了了不起的成就，柯西的心思是前往理工学院学习工程学。1805年，在所有申请入学理工学院的学生中，柯西排名第二。秋季入学时，柯西不得不选定将来他毕业后要进入的公共服务领域。他选择了土木工程，对高速公路和桥梁特别感兴趣。柯西很快就在班上领先，并于1807年以荣誉生身份毕业。然后他申请进入高速公路及桥梁学院进行进一步的学习。在这个学校里，学生只有12月到3月是在课堂中，而其他时间进行实地工作。

1810年，柯西再次以班上顶尖的成绩毕业，成为瑟堡高速公路及桥梁局的一名现场工程师，其工作是建立一个海军基地——拿破仑计划通过这个基地入侵英格兰。在一封写给老柯西的信中，柯西说他前往瑟堡的时候，只带了四本书：维吉尔诗歌全集，肯皮斯的《效仿基督》，拉普拉斯的《天体力学》以及拉格朗日的《解析函数论》。柯西在瑟堡期间的事迹我们知之甚少，只知道拿破仑于1811年5月巡视瑟堡时，柯西曾被介绍给拿破仑。

1812年，柯西回到巴黎，试图寻求一个教学职位以便有收入、有时间去追求其数学理想。这一尝试失败了，而很大部分原因是他一直有病。最后他只好满足于受聘成为一名技术人员参与乌尔克运河的建造。他之前的导师拉格朗日于1813年去世后，柯西申请接替拉格朗日在法兰西学院中数学部门的位置。他没有能赢得此次竞选，而且第一轮就被刷了下来。接下来的两年里，柯西申请了每一个学院中空出来的位置，但都不成功。最终到了1814年末，聊可安慰的是，他获选进入巴黎学者社团。三个月后，正当柯西准备开始教学的时候，随着拿破仑从艾尔巴岛的流放中回到巴黎，法国再次陷入了分崩离析的境地。

1814年，随着波旁王朝的复辟，很多法国的顶尖学院开始开除拿破仑的狂热支持者。柯西试图竞选原来由泊松担任的力学主任一职也没有成功。最后他获得了一个在理工学院教书的职位，一开始作为数学家溥安硕所教授的分析课的“替补”教授。溥安硕身体欠安，三年不能上课。后来柯西获得了分析及力学教授的职位。这是当之无愧的。

柯西最终获得了一个永久职位，他的父母催促他可以结婚了。实际上，他们所做的不止是催促他成家，而且他的父亲还为他挑选了新娘。他的妻子闺名爱洛伊斯·德·比尔，是一位出版社社长的女儿。她带来了丰厚的嫁妆，而他们的婚礼也与他们的社会地位相配。路易十八和所有的皇室成员在他们的结婚证书上签字。

所有迹象表明，柯西对待妻子和女儿们的态度不比对待工艺品强多少，也就是说，必要的时候可以放在一边。他之所以结婚可能只是为了满足他父母布尔乔亚式的要求。他和爱洛伊斯有两个女儿，阿里茜亚生于1819年，玛蒂尔德生于1823年。长大后她们都嫁入豪门。

接受委任后，柯西开始重构理工大学的数学课程，将更多的重点放在纯数学上。他先是集中在微积分（他这方面的工作本书也有节选）。牛顿和莱布尼茨发明了微积分用以解决特定的数学问题。拿牛顿来说，他需要解决的是天体动力学中牵涉到椭圆和抛物线的问题。而微积分在18世纪的发展建立在不稳固的基础上。一个函数的导数被认为是表述该曲线上某一点P的切线的公式的方法。

而一个函数的积分被理解为无穷多个无限小的长方形的面积的和，其中长方形的高是函数值，而宽是以dx表示的一个无穷小量。确实，莱布尼茨引入积分符号：\(\int_a^b f(x)dx\)时，就是因为这个符号很像字母S，也是“求和”单词的首字母。所以，如果我们考虑特定的良构的函数（比如\(f(x)=x^2\)），那么求一个函数的积分的问题就被约简为找到一个特定级数的极限。对于函数\(f(x)=x^2\)来说，其积分就是高为\(x^2\)而宽度为\(dx\)的长方形面积之和。

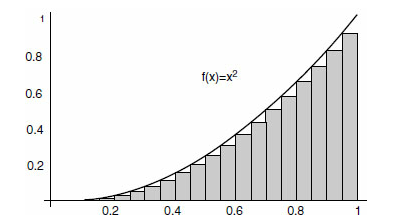
因此，求函数\(f(x)=x^2\)在0到1区间上的积分就是找到下列级数的极限：

\(\frac{(\frac{1}{N})^2+(\frac{2}{N})^2+(\frac{3}{N})^2+...+(\frac{N-1}{N})^2}{N},\,n\rightarrow \infty\)

（其中N趋向无穷。）也就是：

\($\frac{2N^3-3N^2+N}{6N^3}=\frac{1}{3},\, N\rightarrow \infty\)$

当N趋向无穷时的极限。

18世纪早期的数学家们很快发现，积分和求导是互逆的。到18世纪中叶，欧拉和伯努利认为积分无非就是求导的逆运算。实际上，欧拉利用莱布尼茨认为积分是求和的概念只是用来进行积分的近似估计。找到一个函数f(x)的积分公式需要找到另一个函数g(x)使得其导数在任何一点都等于f(x)。因此函数\(f(x)=x^2\)的积分公式就是\(g(x)=x^3/3\)，因为\(f(x)=x^2\)就是\(g(x)=x^3/3\)导数。

柯西于1818年开始在理工学院教书的时候，微积分所赖以建立的基础就是如此。对于良构函数的积分有方法，但是没有积分的理论。也许是受到傅立叶证明任意函数都可以表示为无穷三角函数级数的激励，柯西研究出积分第一定理，不依赖于特定函数，不依赖于微分——他也为之奠定了新的基础，也不依赖于几何直觉。在1821年《分析课程》的引言中，柯西说，他希望带入数学分析的精确度应该能媲美欧几里德在《原本》中所带入的那样。他特别注重于取消所谓的无穷小量，需要对连续性有新的定义。柯西为单变量实函数的连续性做出了如下的定义：

令f(x)为变量x的函数，并假定对于任意给定区间内的每个x值，该函数永远取一个有限值。如果对于该区间内的某个x，将其值增加一个无穷小的增量，函数本身也会得到一个增量，其增值f(x+a)-f(x)同时取决于新变量的值和x的值。如果这点确定，当对于每个区间内的x值，f(x+a)-f(x)的差值会无限地变小，那么函数f(x)在给定区间内对变量x连续。换句话说，如果在该区间内，变量的一个无穷小的增值总是引起函数值本身的无穷小增值，则在该区间函数f(x)对x是连续的。

柯西1823年的《无穷小分析教程概论》的第一部分集中于y=f(x)函数导数的微分。他使用的术语“导数”和符号f'(x)来自他的导师拉格朗日。但是，拉格朗日通常还会继续说导数是一条曲线的切线，必要时去找到某个特定导数的公式。柯西远远超越了拉格朗日，他定义f在x的导数是下式这个差分商在i趋向于0时的极限：\(\Delta y/\Delta x=\frac{f(x+i)-f(x)}{i}\)。

这就是我们现代对于导数的定义，它不依赖于几何。

《概论》的第二部分，柯西集中于积分的概念。

\(\int_a^b f(x)dx\)

其中函数f(x)在a/b之间连续。柯西将区间[a, b]在n点\((x_1, x_2, ..., x_n)\)上加以分割，使得\(a\lt x_1\lt x_2\lt ...\lt x_n\lt b\)。他称：\(x_i-x_{i-1}\)的最大值为区间范值，并考虑如下的求和：

\(S=(x_1-a)f(a)+(x_2-x_1)f(x_1)+...+(x_n-x_{n-1})f(x_{n-1})+(b-x_n)f(x_n)\)

（这一求和现在被称为区间的柯西求和。）利用他自己的连续性定义，柯西证明，对于固定区间[a, b]上连续的函数f(x)，S和S'必定可以任意相近，只要P和P'的范值足够小。这一结论使得柯西可以将积分\(\int_a^bf(x)dx\)定义为当范值P趋向于0时，S的极限。

再次利用他的连续性定义，柯西证明对于任意两个区间P和P'，其对应的求和S和S'可以无限接近，只要P和P'的范值足够小。

定义了积分理论后，柯西就可以继续证明积分和微分之间的内在关系。这在如今作为微积分基本法则为我们所知。它表明，如果G(x)=f(t)从a到x(<=b)的积分，那么G(x)的导数等于f(x)，也就是说G'(x)=f(x)。

虽说柯西能够激励他那些最聪明的学生，他从未学会如何调整课程来适应中等生。这类学生来到学院只是追求增加他们的基础数学知识，来满足——比方说工程学位的需要。由于要在指定的时间内完成柯西的课程实在太野心勃勃了，他们经常会逃课。1821年4月，就在一堂已经拖得不象话的课程的尾声，几个学生喝着倒彩，对着柯西吹起口哨，大摇大摆地走出了课堂。

柯西的《概论》根本没能取悦学院的教师团队，反而激起了他们的恼怒——因为太理论了，太不切实际了。事实上在1823年末，内务部部长指派了一个委员会（其中包括拉普拉斯和泊松）来确保数学教育与工程学学子的需要相协调。这10年剩下的时间里，学院的行政部一直监督着柯西的教学，确保其对工程学生来说是合适的。

路易十八统治时期，法国迎来了相对和平与稳定的时光。路易十八于1824年去世后，他的弟弟查理十世继位并试图恢复君主权力到革命之前的那个样子。随着对共和的同情席卷了法国，政府试图对其加以控制，并呼呼来自那些保皇组织的支持。作为铁杆保皇派和天主教徒，柯西是其中一个组织—天主教义保护协会—的发起人之一。

1830年的7月革命推翻了查理十世，改推其表弟奥尔良公爵路易-菲利普为皇帝。和所有政府官员一样，学者们被要求宣誓效忠。柯西拒绝如此做，而且他还流放了自己——也许是担心新政权会迫害像他这样的忠诚的天主教徒。柯西毫无悬念地丢了工作。

柯西把老婆孩子留在了法国，他先是和一群耶稣会士住在瑞士边境的弗里堡。会士们很快将他推荐给撒丁王——他们的恩主之一，而撒丁王向他提供了都灵大学的教授职位。但是柯西只在那里待了三年多一点时间，就受邀前往布拉格，与被流放的查理十会合，并教授王太子。直到此时柯西才将他的家人接来团聚，他们已经分别四年了。

查理十世褒奖柯西的方式是将他擢升为男爵。1838年，查理十世去世，而王太子也在他18岁那天完成了他的教育。为皇室效力完毕后，柯西回到了巴黎，这肯定是受到他母亲健康状况日渐恶化的迫使。流放后的柯西失去了教学职位，他唯一能重新开始的职位是作为科学院的成员。幸运的是，他以前的老师普罗尼在柯西回来后不到一年就去世了，而柯西获选继任他老师曾担任的经度局几何教授一职。

此时政治局势也趋缓和，学者们不用再宣誓效忠。柯西对新政权的冷淡虽然说不至于要了他的命，但肯定影响了他的事业，让他丢了几个在政府资助的机构中任美差的机会。1843年，法兰西大学的数学系主任职位空缺，柯西是三个候选人之一。虽然说他肯定是最出色的候选人，但柯西特别保皇的态度以及他对耶稣会的同情使得很多投票者头了反对票。最终，在24名成员的委员会中，他只得到3票。柯西为此结果而感到受辱，宣布只要有任何可能他会落选，他不再允许他被提名竞选任何职位。

1838年到1848年期间，他没有担任任何教职。他唯一的在科学院的职务为他提供了一个平台呈现他的工作。他也恪尽职守，在这10年间总共向院里提交了240篇文章和研究。1848年的2月革命推翻了路易-菲利普。柯西盼望他以前的学生波尔多公爵，如今的尚博尔伯爵可以继承王位。但实际情形并非如此。第二共和国替代了路易-菲利普。虽说称不上是个共和党人，柯西还是从共和国废除宣誓效忠的做法中得益。很快他赢得竞选，担任了巴黎大学的校长。1852年拿破仑三世登基，他免除了柯西的宣誓义务。

柯西一生都辛勤工作，发表了789篇数学和科学论文。他的全集于1882年开始发表，直到1970年发表的第27卷（也是最后一卷）才结束。他才华横溢的贡献直到他于1857年5月23日逝世才告终结，他死于风湿病急性发作。