魏尔斯特拉斯(Karl Weierstrass,1815-1897)——生平与成就

设想一下,成为一名数学家,你的名字注定万世流芳。这当然不错。再设想一下,假定你职业生涯的前12年不得不在高中教书,不只教数学,还要教书法甚至体育。魏尔斯特拉斯的自传中就有这么一部分,甚至他本人在回忆的时候也只能用“无尽的凄凉和厌倦”的时光来描述。每个ε都有一个δ!
魏尔斯特拉斯于1815年10月31日生于威斯特伐利亚的奥斯滕菲尔德(现在属于德国),此时距威灵顿在滑铁卢击败拿破仑刚过四个半月。魏尔的祖先没有什么知识方面的成就,更不用说数学方面的伟业了。他是维尔海姆和西奥朵拉(娘家姓冯德福斯特)的长子。对他母亲的家庭我们所知甚少,只知道和魏尔斯特拉斯家一样,是温和的天主教徒。我们知道他父亲在艺术和科学方面受过良好的教育。维尔海姆的职业是当时普鲁士政府中威斯特伐利亚的一名小职员。他八岁的时候,开始做税务工作并不断转行。魏尔的家庭生活已然杂乱,却又转向更糟糕更严重的一面:他的母亲突然于1827年逝世。此时他又有了两个妹妹和一个弟弟。老魏尔两年后再婚,给小魏尔的生活又带来了一个新的烦恼。
1828年,魏尔进入隶属威斯特伐利亚的帕德伯恩镇上的天主教高中学习。因为他的父亲来到此地从事一份新的工作:助理税务官,所以必须将新家设在这里。魏尔家的经济情况一定很艰难。在14岁那年,小魏尔为一个当地商人之妻工作,作为图书管理员。他的父亲认为这样能给小魏尔一个机会,发挥他的数学本领!老魏尔怎么也想不到,这给了小魏尔一个机会,用闲暇时光读了学校发行的《纯数学和应用数学期刊》的拷贝。这可是全欧洲最顶尖的数学期刊啊!读完这些文章后,小魏尔立志要成为一名数学家。
但老魏尔有别的打算。尽管1834年小魏尔高中毕业时已经赢得了很多数学奖项,老魏尔坚持让小魏尔在附近的玻恩大学就读一个公共财经和行政专业。小魏尔很不情愿的答应了。在玻恩的四年,沉重的生理和心理压力围绕。小魏尔经常以酗酒来放纵自己,用击剑作为反叛的表示。有好几次,在击剑对抗中,他都差点受伤。
长长的四年过去了,魏尔甚至没有等到学位考试就离开了玻恩。他的父亲为此狂怒不已。在大学待了四年,小魏尔离小职员的位置还是那么遥远。不到一年,一位家族朋友建议了一个合理的让步方案:小魏尔可以就读附近明斯特上的神学及哲学学院,并只要用一年时间就可以进行教职考试。
一年后的1840年,魏尔确实进行了考试,并在数学考试上要求用特别困难的问题来考他。魏尔不知道他回到这个问题有多么的出色。校方只是告诉他通过了数学考试,其它考试也通过了。他们甚至懒得告诉他,数学考试的校外审阅人是数学家古德曼——他曾是伟大的高斯的学生。古德曼意识到魏尔在考试中给出的答案为椭圆函数理论这一数学分支做出了重要的进步。但是有将近十年,魏尔都没能知道对他的赞誉。
于是,魏尔开始了他为期十五年的教授数学的职业生涯,面对的是毫无兴趣的学生,同事水平也不高,根本无人拥有哪怕只是他一丁点的才华。好笑的是,魏尔第一篇研究论文发表在学校的招生说明书上,本意是让那些为孩子们找地方读书的父亲们感兴趣。我们只能想象这些父亲的反应会是怎样。他们读到的数学对他们而言根本无法理解,因为它们是如此的有开创性!
为了在沉闷单调的大学生活中保持他的清醒,魏尔专注于研究他能找到的任何当代数学。常年这样的压力是有代价的。到1850年,魏尔开始患上持续的眩晕,时间可以长达一个小时,只有剧烈呕吐后才会停止。
但是他离成功也不远了。1854年,魏尔终于向《纯数学和应用数学期刊》提交了他的论文《论阿贝尔函数理论》。这一时间是他生命中的分水岭。魏尔终于获得了他应得的注意。柯尼斯堡大学(现但泽大学)授予他名誉博士学位。为了留住他,布劳恩斯贝格大学在1855年提拔他为高级讲师,还提供了为期一年的休假。但是魏尔期望更多——一个真正的大学职位。1855年,他以年届不惑之身第一次申请大学教职,希望成为东普鲁士布雷斯劳(现波兰弗罗茨瓦夫)大学的数学教授。他没能成功,不过各种要约随之如潮水般涌来。
1856年他又发表了一篇关于阿贝尔函数的论文。不久,他参加了在维也纳的一个会议,并且让他挑选任何一所奥地利大学教授职位。当时,奥地利数学停滞不前,因此魏尔犹豫不决。然后柏林工业学院为他提供了一个教授职位。魏尔知道那不是最出名的学院,但是总强过奥地利啊!
但是,毕竟还不如著名的柏林大学好。也许是命运使然,就在他接受工业学院的要约后不久,柏林大学为他提供了一个副教授的职位。他虽然很想接受柏林大学的要约,魏尔知道他必须先完成他对工业大学做出的为期七年的承诺。虽然工业学院还算不上德国高等教育学院中最著名的,学院最终还是为魏尔提供了一个机会,来进行研究并向那些求知若渴的学生们讲授。
魏尔的研究中,最出名的是我们现在所知的“ε法”,本书有选入。魏尔最早在1859-1860学年,题为《分析引论》的课程中开始他的ε法研究。ε法为数学家提供了一个精确的方法,研究一个无穷数列或者级数趋向极限的概念。举一些例子可以帮助我们展示魏尔的ε法有多强大。
考虑这个等比数:首项为1,然后各项都是前项的1/2,直到“无穷”:
\(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+...\)
不少读者应该记得,等比数列有限项求和的公式:
\(a\sum_{k=0}^{n-1}r^k=a\frac{r^n-1}{r-1}\)
这个公式可以应用到n为任意有限值的情形。在上式中令\(a=1,r=\frac{1}{2}\),得到:
\(\frac{1-\frac{1}{2}^n}{1-\frac{1}{2}}\)
数学家从直觉出发认为,这个式子的分子在n趋向无穷的时候,会趋向1,因为\(\frac{1}{2}^n\)在n趋向无穷时,趋向于0。但是“n趋向无穷”是什么意思?自古希腊数学家和哲学家埃利亚的芝诺(死于约公元前425年)以来,这个问题就困扰着众多数学家和哲学家。
魏尔的ε法提供了解决方案:n不再需要趋向无穷。相反,极限的定义是在n趋向无穷的过程中定义的。魏尔这样定义一个无穷序列有极限:对于任意给定的ε,可以找到一个整数n,对于所有大于等于n的整数m,序列的第m个元素与极限的差都在ε之内。注意到ε法很容易用在上述问题,证明\(\frac{1}{2}^n\)的极限在n趋向无穷时为0。对于任意ε,只要找到1/2的某次方小于ε,那么很明显,更高次方都会比ε小。
ε法对函数理论有更大的影响。19世纪中叶之前,数学家们注重的函数是这样的,比如正弦函数,它们可以至少在部分不用提笔就可以画出,或者即使提笔也最多偶尔提一下。这是连续性的一个非常几何化的概念。
ε法解放了数学家,不用再用如此几何的方式来思考连续问题。魏尔对于在点x0函数f连续的定义为:
如果对于每个ε,可以找到一个δ,使得只要x在\(x_0\)的δ范围内,\(f(x)\)也在\(f(x_0)\)的ε范围内,那么f在点x0处连续。
这个定义当然符合我们直观的概念,要在一个点附近画出一个连续函数,你必须足够接近那一点的函数值。但是还可以做的更多。
19世纪初,德国数学家狄利克雷定义了两个很怪的函数。第一个Χ(x)函数,称为特征函数,表明实数范围内一个数的有理性。它取值如下:
- Χ(x)=1,如果x是有理数
- Χ(x)=0,如果x是无理数
第二个函数,不出所料地称为狄利克雷函数,D(x),更奇怪。它取值如下:
- D(x)=1/b,如果x是有理数,且可以用最简分式表示为a/b
- D(x)=0,如果x是无理数
这些函数都不能像正弦函数那样被“画出”。对第一个函数这不奇怪,因为它处处不连续。(比如取ε<1。总有一个临点其值要差1,因为无理数和有理数在各处都是交错的。)
不是所有的数学家一开始就能在这些怪兽函数中发现有什么价值。20世纪初,伟大的法国数学家庞加莱对这个函数还有别的一些函数发出抱怨说:
有时,逻辑会产生怪物。半个世纪以来,我们见识了古怪的函数登基。这些函数看起来试着让自己不能表示什么,不像那些老实的函数,至少还有点用。
1861年,初次形成ε法后的两年,魏尔证明狄利克雷函数D(x)在任意无理数值x上连续。假定我们要这样应用ε-δ法:取\(x=\sqrt 2\),ε=0.1(1/10)。我们知道\(D(x=\sqrt 2)=0\)。那么δ要取怎样的值,使得所有x在\(D(x=\sqrt 2)=0\)的δ范围内,D(x)的值,与0.0(\(D(x=\sqrt 2)=0\))的差不超过0.1(我们选定的ε)?
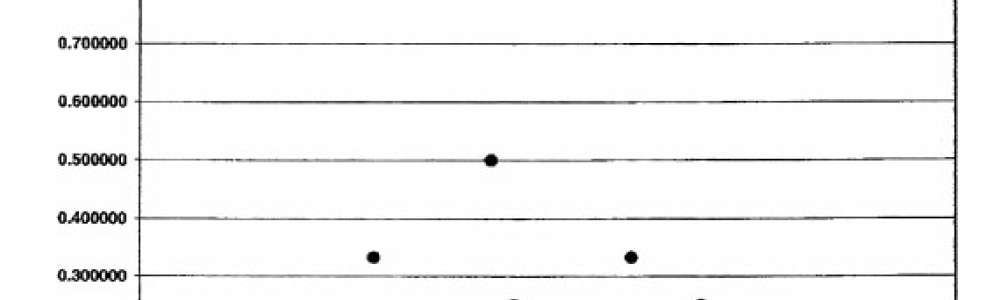
这个证明异常直观。如果我们意识到,D(x)取值大于0.1的有理数只能是分母不超过10。所有这些靠近\(x=\sqrt 2\)的有理数可以列出,并找到最靠近的那个。幸好我们有表格!下面这张图,列出了所有1.0到2.0之间,而且其分母不超过10的有理数的D(x)值:
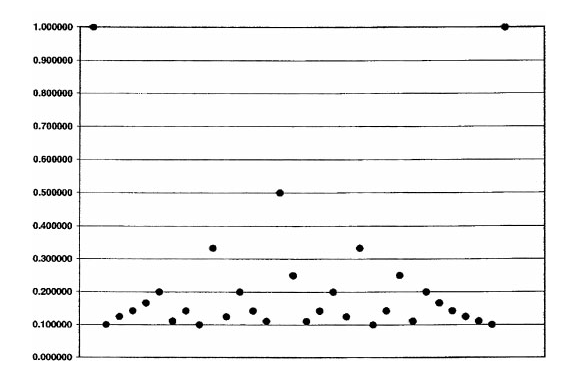
我们发现,这个实数x=1.30(13/10),其D(x)最接近于0。
柏林的数学活动一开始的大爆发累垮了魏尔。1859-1861年间的开创性研究后不久,魏尔患上了由“脑痉挛”引起的全面崩溃。最后,他休了一年假,不光不教书,也不进行数学研究。1863年他回来后,他总是坐着进行演讲。一位高年级学生负责劳动,在黑板上写公式。
最终,经历了八年之久,他终于转到备受敬仰的柏林大学。作为一贯的完美主义者,且对自己的体力珍惜有加,魏尔直到1880年代中期才发表了他的ε法。不出所料,德国最伟大的一代数学学子进入柏林大学,拜倒在魏尔门下,只有在那里才能第一手地学到ε法。
康托(他的生平和成就稍后谈到)也许是魏尔的学生中最伟大的那个。康托的成果也成为魏尔和他的一位最老也是最好的朋友克罗内克——正是他说出了这句名言并为我们引来作为本书标题,“上帝创造了整数,其它则是人的工作”——之间产生摩擦的原因。克罗内克可以接受所有类型的数:有理数,实数,甚至虚数。但是他不能接受无穷——康托成果的重点。克罗内克就是认为康托的无穷数学对象不能存在,他的工作也就没有意义,没有用处。
除了研究数学,魏尔的晚年并不开心。和很多数学家一样,魏尔终生未婚。他的弟弟和两个妹妹也都未婚。魏尔生命中的最后三年都在轮椅上度过,完全依赖于别人,自己无法行动。他81岁生日后的几个月的1897年初,他逝世于柏林。
伟大的法国数学家庞加莱——他之前抱怨过诸如狄利克雷函数这样的怪物的涌现——对魏尔斯特拉斯有着极高的评价。庞加莱认为魏尔斯特拉斯位居十九世纪最伟大的数学家中的第三位。前两位当然是无法比肩的高斯和无法估量的黎曼。