题目
分析
离散化和稀疏
本题引入了“离散化”这个概念。以本题为例,最自然的做法是开一个数组,然后根据每个“染色”(着火)的范围加以操作,最后遍历累加染色的位置即可。但,本题的特色是:
- “着色”范围的取值范围很大:\(a_i, b_i \in [-2^{31}, 2^{31}]\),已经接近
int的范围 - 而着色范围的数量很小:\(n\le 20000\)
显然,最终着色区间的总长度的计算只和n个范围有关。而且,最终着色的地方与整个数轴相比,是非常“稀疏”的。
因此,我们只要保存处理这n个区间即可。
区间的覆盖与更新
将所有的区间按照“左边界优先然后右边界”的方式进行排序,可以形成一个由左向右的排列。
区间之间有不同的覆盖关系:

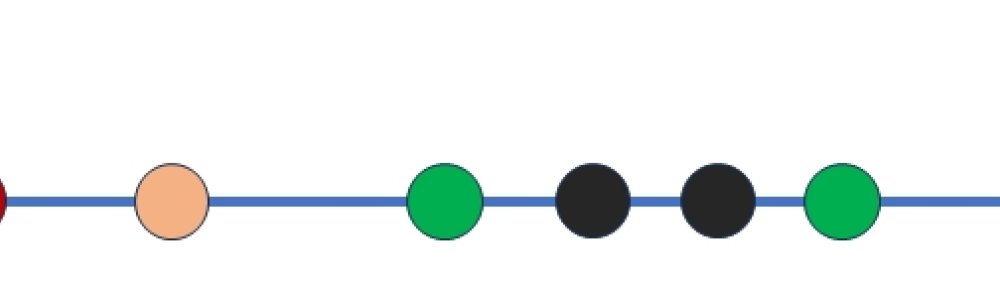
- 不重叠:如图中红色区间与绿色区间:\(a_绿\ge b_红\),也即是绿色区间完全在红色区间的右边(最多就是绿色左边界与红色右边界重合)。
- 此时,红色区间已经可以计算,其覆盖的长度就是\(b_红-a_红\)。
- 同时,需要更新区间新的范围:新的区间范围改为\([a_绿, b_绿)\)。
- 如图中
- 部分重叠且右边界扩展:红色区间和黄色区间:\(a_黄\lt b_红\),两个区间必定有重合。此时如果\(b_黄>b_红\),那么黄色区间与红色区间只有部分重合:那么需要更新区间为\([a_红, b_黄)\),以反应新的区间长度。但此时不必计算覆盖范围。
- 完全包含:绿色区间和黑色区间:\(a_黑\lt b_绿\)而且\(b_黑\lt b_绿\),黑色区间完全在绿色区间中。那么不需要修改区间范围,也不必计算覆盖范围。
- 无论如何,看下一个范围再做判定。
- 区间遍历完毕后,有可能最后一个区间也被完全包含在前一个区间中,所以要最终计算一下。
下面给出核心的C++代码:先排序再线性合并重叠区间,使用long long避免溢出。
sort(seg.begin(), seg.end()); // sort by left then right
long long ans = 0;
if (!seg.empty())
{
long long L = seg[0].first;
long long R = seg[0].second;
for (size_t i = 1; i < seg.size(); ++i)
{
long long a = seg[i].first;
long long b = seg[i].second;
if (a < R)
{
// overlap (left-closed, right-open): merge when a < R
if (b > R)
R = b;
}
else
{
// disjoint or just touching (a >= R)
ans += R - L;
L = a;
R = b;
}
}
ans += R - L;
}
答案

思考
复杂度评估:
- 时间复杂度:排序消耗\(O(n log n)\),合并扫描消耗\(O(n)\),因此总体为\(O(n log n)\)。
- 空间复杂度:主要用于存储区间数组,额外开销为\(O(n)\)(若就地排序则额外为\(O(1)\))。
关于离散化的补充说明(重要点):
- 何时使用离散化?
- 当坐标范围极大或坐标不是小范围连续整数时(例如本题的 \(a_i,b_i\) 可能接近
int边界),直接按坐标建表会浪费内存或不可行。离散化只保留与答案相关的关键点(区间端点及其相邻位置),将坐标映射到\(0..O(n)\)索引,从而在压缩后的坐标上使用差分/线段树等数据结构。
- 当坐标范围极大或坐标不是小范围连续整数时(例如本题的 \(a_i,b_i\) 可能接近
- 离散化的步骤要点:
- 收集所有区间端点(通常还需收集端点的右侧相邻位置,视闭/开区间而定),去重并排序,得到关键坐标数组
seg(ment)s。 - 用二分或哈希把原区间端点映射到
segs的索引空间;注意保留每个相邻坐标段的实际长度信息(segs[i+1]-segs[i]),因为离散化后相邻索引间的“距离”不再是 1。
- 收集所有区间端点(通常还需收集端点的右侧相邻位置,视闭/开区间而定),去重并排序,得到关键坐标数组
- 闭区间与开区间的细节:
- 在离散化时必须明确原问题中区间是左闭右开还是左右都闭。合并思路中我们用的是左闭右开(即区间\([L,R)\)),并用\(a \lt R\)来判断重叠;如果题目要求闭区间\([L,R]\),需要在处理或离散化时把右端点做
+1的偏移以避免边界混淆。
- 在离散化时必须明确原问题中区间是左闭右开还是左右都闭。合并思路中我们用的是左闭右开(即区间\([L,R)\)),并用\(a \lt R\)来判断重叠;如果题目要求闭区间\([L,R]\),需要在处理或离散化时把右端点做
- 离散化后的差分/扫描线实现:
- 将每个原区间的离散索引区间记为\([i, j)\),对\(diff[i] += 1, diff[j] -= 1\),完成所有区间后做前缀和得到每个离散段的覆盖次数,再乘以该离散段的实际长度累加覆盖总长。
- 实现注意事项:
- 坐标差(\(segs[i+1]-segs[i]\))可能很大,应使用
long long储存并在累加时使用64位整数。排序后使用stable sort或默认sort均可,但建议在插入数据前对区间做边界检查(例如保证\(a\le b\))。
- 坐标差(\(segs[i+1]-segs[i]\))可能很大,应使用