Table of Contents
题目
分析
这道题目我参考了洛谷的题解。
应该说,这题的思路比较直观,但需要考虑各种不同的情形。
总体思路是:无论障碍点如何分布,一个可能的最大的矩形一定是以障碍点(包括四个边界)作为边界的。
第一次扫描:从左到右
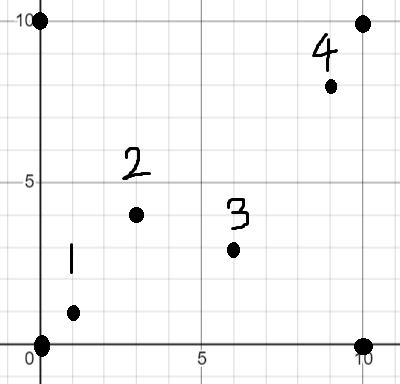
这个扫描需要双重循环:按照x坐标从左到右确定一个左边界(外循环),然后不断向右找一个点作为右边界(内循环)。在循环过程中,不断计算包围的矩形的矩形面积,同时调整边界点的位置作为后续的约束。
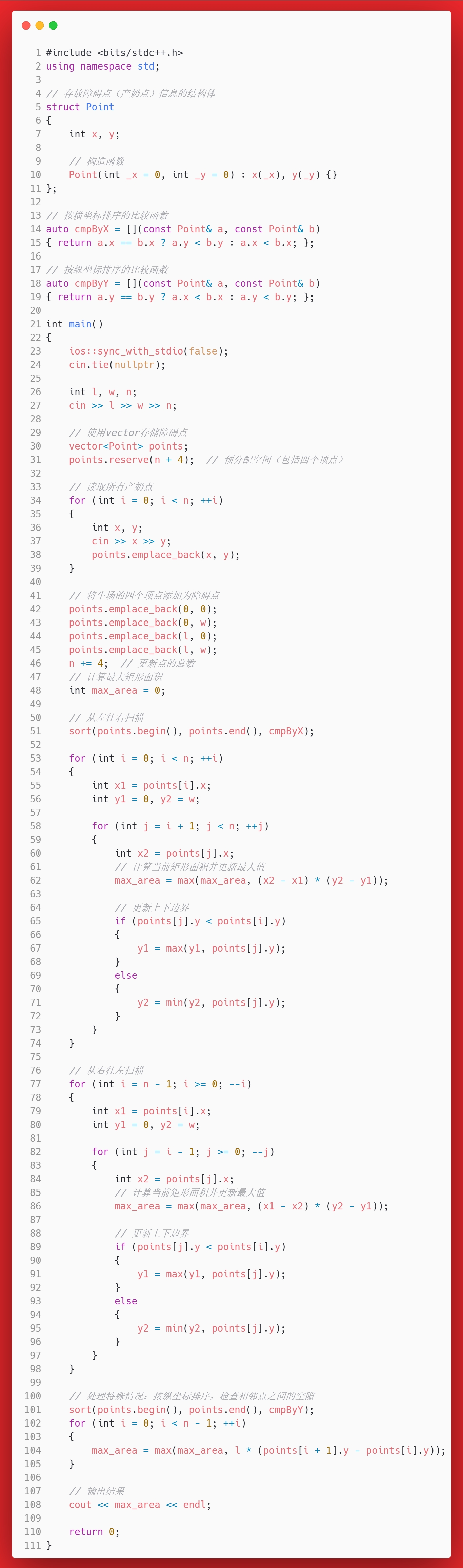
核心代码为:
sort(points.begin(), points.end(), cmpByX);
for (int i = 0; i < n; ++i)
{
int x1 = points[i].x;
int y1 = 0, y2 = w;
for (int j = i + 1; j < n; ++j)
{
int x2 = points[j].x;
// 计算当前矩形面积并更新最大值
max_area = max(max_area, (x2 - x1) * (y2 - y1));
// 更新上下边界
if (points[j].y < points[i].y)
{
y1 = max(y1, points[j].y);
}
else
{
y2 = min(y2, points[j].y);
}
}
}第二次扫描:从右到左
第一次扫描可能会漏掉一种情形:极大子矩形的左边界是牛场的左边界,右边界覆盖一个障碍点的情况。
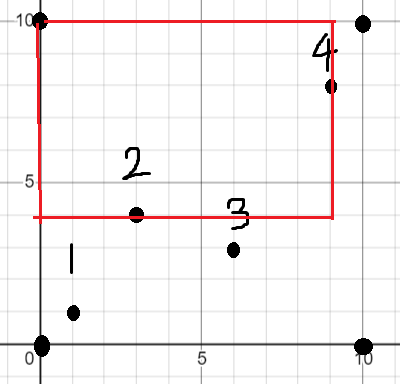
基本思路一样,只是外循环从右往左进行,而内循环改为向左拓展。
第三次扫描:按照纵坐标y的扫描
在从左往右搜和从右往左搜后我们发现还有一种情况没有考虑到,就是极大子矩形的左右边界分别是牛场的左右边界。
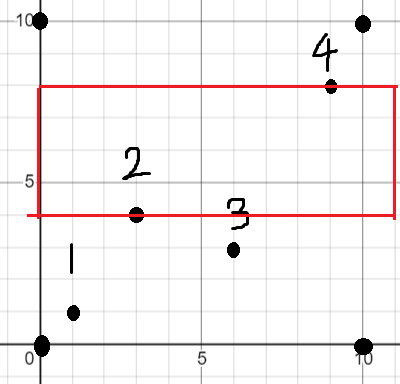
综合上述三种情形,就可以得到最后的答案。
答案
思考
这个算法的核心思想是:通过枚举矩形的左右边界(两个障碍点的x坐标),然后动态维护上下边界(根据障碍点的y坐标),从而找到不包含任何障碍点的最大矩形。
算法的时间复杂度是\(O(n^2)\),其中\(n\)是障碍点的数量。这比暴力枚举所有可能的矩形(\(O(n^4)\))要高效得多。
