题目
分析
这是一道典型的(二维)前缀和应用。
解题包括两个核心函数。一个用来构造前缀和数组,一个利用该前缀和数组来计算当前点位覆盖的正方形的权值。
二维前缀和数组
结合之前的题目(如[P1719:最大加权矩形]),我们再次梳理前缀和数组的构造。首先是原始的权重矩形:
i/j 0 1 2 3 4
0 a b c d e
1 f g h i j
2 k l m n o
3 p q r s t显然,对于[3, 3]这个位置(s),它对应的前缀和按照定义是\(a+b+c+...+r+s\)。而按照前缀和的计算公式(以一维为例):\(prefixSum_i=prefixSum_{i-1}+value[i]\),prefixSum[i]表示的是一直求到下标为i为止。对于0基的一维数组而言,永远存在一个“特例”:prefixSum[0]需要进行约定。而到了二维矩阵,我们也需要进行类似的操作,而且有三个方向的“向前看”:上一行同一列、同一行左边一列以及左上角三个之前算好的前缀和。参照其他算法的思路,我们可以添加一个0行0列,同时将前缀和数组整体变成1基。这样一来,可以直接“向前看”并简化公式:
prefixSum[i][j] = map[i - 1][j - 1] +
prefixSum[i - 1][j] +
prefixSum[i][j - 1] -
prefixSum[i - 1][j - 1];这里,本身单元格的值来自map数组,而map还是0基的,而且两个循环都是从1到等于N。完整的代码如下:
vector<vector<long long>> buildPrefixSum(const vector<vector<int>>& map)
{
int N = map.size();
int M = map[0].size();
vector<vector<long long>> prefixSum(N + 1, vector<long long>(M + 1, 0));
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
prefixSum[i][j] = map[i - 1][j - 1] +
prefixSum[i - 1][j] +
prefixSum[i][j - 1] -
prefixSum[i - 1][j - 1];
}
}
return prefixSum;
}计算一个矩形的权重
基于上述的构造前缀和的方式:map(存放原始权重)为0基,prefixSum(存放前缀和)为1基,在回头求某个矩形\(([x_1, y_1], [x_2, y_2])\),我们也要进行偏移:
long long currentSum = prefixSum[x2 + 1][y2 + 1] -
prefixSum[x1][y2 + 1] -
prefixSum[x2 + 1][y1] +
prefixSum[x1][y1];这里特别注意:以上的坐标都进行了0基到1基的转换。但x1/y1看起来没有变化,是因为在根据前缀和还原区间和的时候有个-1的操作。以一维为例:\(\text{sum}[L, R]=prefixSum[R]-prefixSum[L-1]\),所以x1(y1)+1-1=x1(y1)。
完整的代码如下。注意:这里的循环是从0到N-C/M-C,也就是从0开始。
pair<int, int> findOptimalPosition(const vector<vector<long long>>& prefixSum,
int N, int M, int C)
{
long long maxSum = LLONG_MIN;
int bestX = 0, bestY = 0;
// 遍历所有可能的左上角位置
for (int i = 0; i <= N - C; i++)
{
for (int j = 0; j <= M - C; j++)
{
// 计算以(i,j)为左上角的C×C正方形的价值和
// 使用前缀和公式:sum = S(x2,y2) - S(x1-1,y2) - S(x2,y1-1) +
// S(x1-1,y1-1)
int x1 = i, y1 = j; // 左上角
int x2 = i + C - 1, y2 = j + C - 1; // 右下角
long long currentSum = prefixSum[x2 + 1][y2 + 1] -
prefixSum[x1][y2 + 1] -
prefixSum[x2 + 1][y1] +
prefixSum[x1][y1];
if (currentSum > maxSum)
{
maxSum = currentSum;
bestX = i + 1; // 转换为1基索引
bestY = j + 1; // 转换为1基索引
}
}
}
return make_pair(bestX, bestY);
}答案
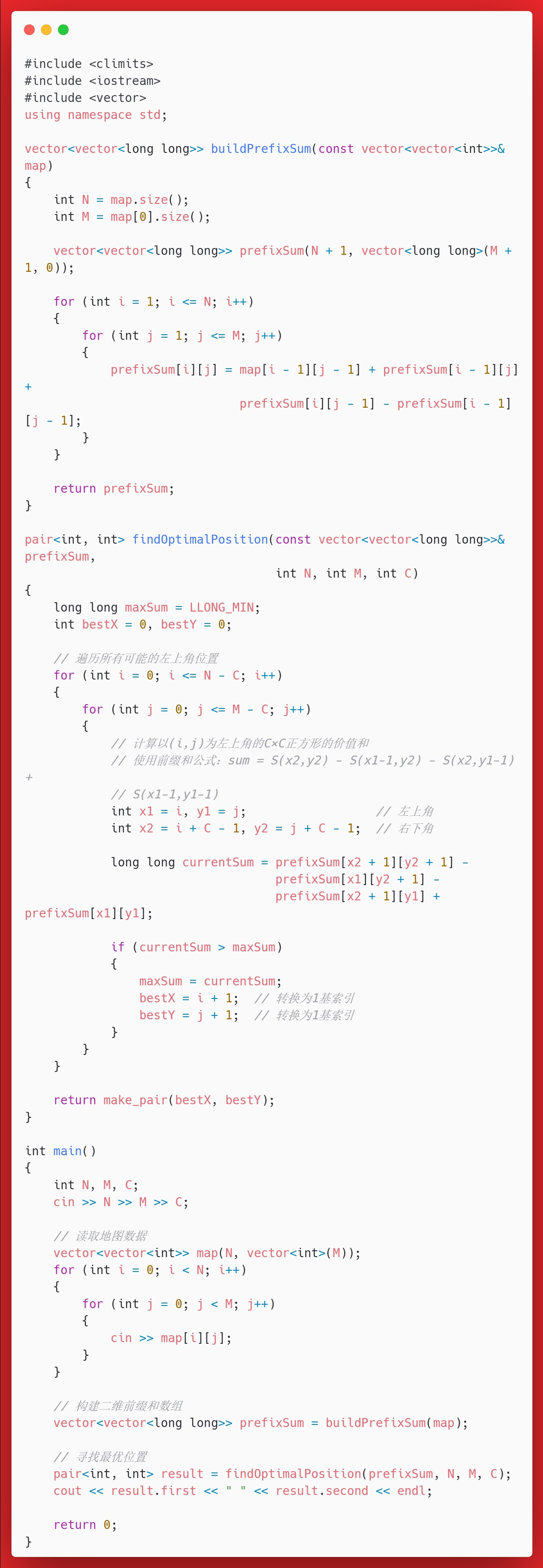
思考
通过本题,我们可以比较透彻地了解二维矩阵中前缀和、以及某个子矩阵权重求和的计算方式,特别是其中涉及的0基(原始权重数组)和1基(前缀和数组)操作手法,是需要重点关注的。
请参考P3017:Brownie Slicing,那里使用了更直观的统一1基数组处理。两者都有优缺点,竞赛时建议采用统一1基数组方式。
