题目
分析
这是一道典型的“单调队列”应用题。
有关“单调队列”的说明,可以参考这篇文章。它可以用来解决“区间内最值”等问题。
整体的解题思路是:
- 对于\(a\times b\)大小的矩阵而言,取一个\(n\times n\)的正方形,横向可以有\(b-n+1\)个;纵向可以有\(a-n+1\)个。——这个也决定了单调队列中滑动窗口的数量。
- 我们针对行和列各自维护两个单调队列:
row_max/row_min,存储每行滑动窗口的极值;col_max/col_min,存储每列滑动窗口的极值。这是由于我们最终要求\(n\times n\)大小的正方形中最大-最小的差决定的。这个方法,将一个二维的极值问题退化为两个一维的极值问题。同时,需要注意,这么处理的过程有个先后,所以先处理完行后,在处理列的时候,是要在经过行处理退化后的矩阵中进行。 - 一旦获得了
col_max和col_min,就可以对应地求出差,并通过打擂台方式保存最小的差。
按行的退化
这可以通过deque来实现,代码也非常“标准”:
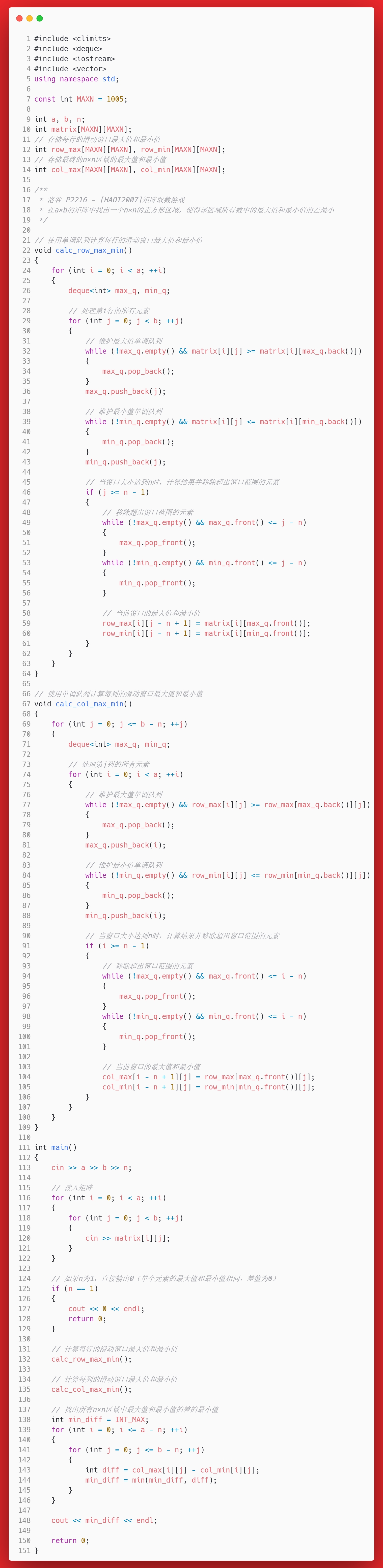
// 使用单调队列计算每行的滑动窗口最大值和最小值
void calc_row_max_min()
{
for (int i = 0; i < a; ++i)
{
deque<int> max_q, min_q;
// 处理第i行的所有元素
for (int j = 0; j < b; ++j)
{
// 维护最大值单调队列
while (!max_q.empty() && matrix[i][j] >= matrix[i][max_q.back()])
{
max_q.pop_back();
}
max_q.push_back(j);
// 维护最小值单调队列
while (!min_q.empty() && matrix[i][j] <= matrix[i][min_q.back()])
{
min_q.pop_back();
}
min_q.push_back(j);
// 当窗口大小达到n时,计算结果并移除超出窗口范围的元素
if (j >= n - 1)
{
// 移除超出窗口范围的元素
while (!max_q.empty() && max_q.front() <= j - n)
{
max_q.pop_front();
}
while (!min_q.empty() && min_q.front() <= j - n)
{
min_q.pop_front();
}
// 当前窗口的最大值和最小值
row_max[i][j - n + 1] = matrix[i][max_q.front()];
row_min[i][j - n + 1] = matrix[i][min_q.front()];
}
}
}
}
这里,我们在同一个代码段中,完成了最大、最小极值队列的维护,因为两者所关注的窗口一样,只是弹出的条件不同。最大队列的弹出标准是:matrix[i][j] >= matrix[i][max_q.back()],而最小队列的弹出标准是:matrix[i][j] <= matrix[i][min_q.back()]。
按列的退化
完成上述退化后,按列的退化也是类似的,但此时操作的矩阵应该是我们刚完成的row_max/row_min矩阵,得到的是col_max/col_min矩阵。
计算差值并维护最小值
完成上述两步的退化后,对col_max/col_min进行遍历即可:
// 找出所有n×n区域中最大值和最小值的差的最小值
int min_diff = INT_MAX;
for (int i = 0; i <= a - n; ++i)
{
for (int j = 0; j <= b - n; ++j)
{
int diff = col_max[i][j] - col_min[i][j];
min_diff = min(min_diff, diff);
}
}答案
思考
单调队列具有“求区间极值”的特性,而且时间复杂度大大降低。本题中,通过两次“退化”——将二维矩阵的处理转为两次一维矩阵——完成了任务。
特别地,如果滑动窗口的大小是1——在本题中就是选择1*1的窗口,那么不用进行计算,答案必定是0。
