本页面已浏览72次
Table of Contents
1. Year of the Cow
Farmer John的奶牛们得知最近正在庆祝牛年的到来时十分兴奋。牛年总是奶牛们的最爱。
我们知道,中国历法中每一年所对应的生肖遵循12年的周期:Ox, Tiger, Rabbit, Dragon, Snake, Horse, Goat, Monkey, Rooster, Dog, Pig, Rat(牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪、鼠),然后回到牛。
奶牛Bessie自豪地说她是在许多年前的一个牛年出生的。她的朋友Elsie想要知道她与Bessie出生相差多少年,并且希望你能够通过查看农场上若干奶牛出生年份之间的关系来帮助她推算。
输入格式(从终端 / 标准输入读入):
输入的第一行包含一个整数N($1\le N \le 100)。以下N行每行包含一个8个单词的短语,指定了两头奶牛的出生年份之间的关系,格式为
"Mildred born in previous Dragon year from Bessie"(Mildred在Bessie出生的前一个龙年出生),或"Mildred born in next Dragon year from Bessie"(Mildred在Bessie出生的后一个龙年出生)。最后一个单词是农场上某一头奶牛的名字,为"Bessie"或一头已经在之前的输入中出现过的奶牛。
第一个单词是农场上某一头奶牛的名字,不为"Bessie"且未在之前的输入中出现过。所有的奶牛名字不超过10个字符,且仅包含字符
a..z或A..Z。第5个单词是上述十二生肖之一。
第4个单词是"previous"(之前)或 "next"(之后)之一。例如,如果短语为
"Mildred born in previous Dragon year from Bessie",则 Mildred的出生年份为最为接近且严格处于Bessie的出生年份之前(不同年)的龙年。
分析
这个问题很有意思!涉及到中国的生肖排列!
当然,这个问题不算太难,涉及了字符串操作以及求余计算——涉及“循环往复”的数据时,往往用到求余。
基于题意,每次我们都可以得到一头新的奶牛的名字,它与另一头牛的出生关系,进而推算出和Bessie的出生关系。出于方便,我们可以假定Bessie出生在2021年(或者任意一个牛年)。
我们先看如何处理那个比较长的描述语句(类似Mildred born in previous Dragon year from Bessie)。这样的语句其实很有规律,每个部分都有严格的含义。我们只要分别提取加以处理即可:
cin >> cowa >> born >> in >> relation >> animal >> year >> from >> cowb;我们真正关心的并对我们编程有用的,其实只有cowa, relation, animal, cowb这几个变量罢了。
其次,我们知道了这个关系后,就可以得到cowa的出生年份了。这里有两个寻找方向。如果relation是next,那么我们增加cowa的出生年份,直到它的出生年份是animal为止。反则反之。
最后一个问题,就是在上面的问题中,如何判定某个年份是哪个生肖了。这个也不复杂。我们可以从Bessie的出生年开始,根据这个animal的出生年份,向前或者向后一个一个搜索。
答案
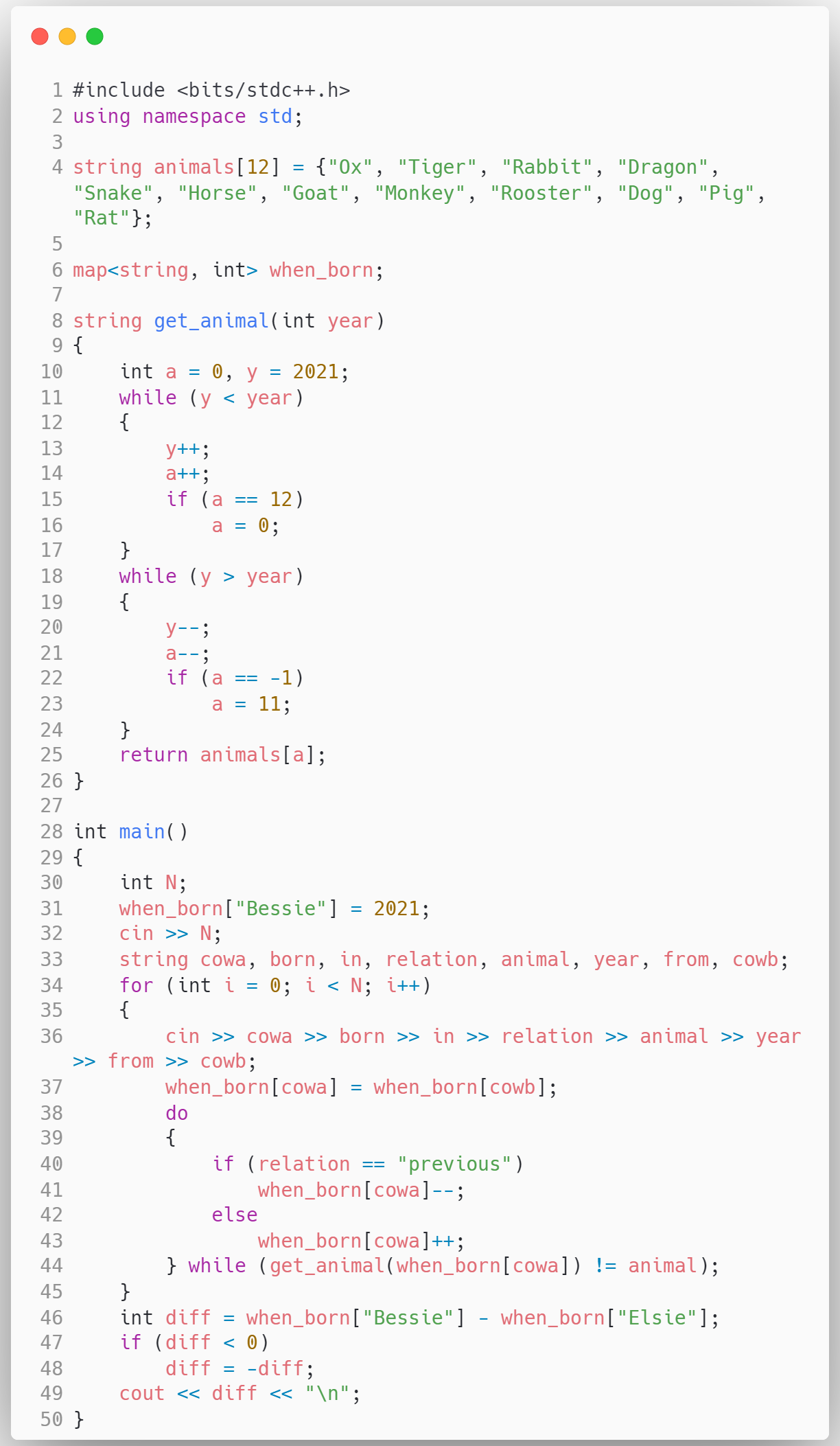
思考
这个解法中,没有考虑“提前终止”的可能性。例如,以样例的输入来看:
4
Mildred born in previous Dragon year from Bessie
Gretta born in previous Monkey year from Mildred
Elsie born in next Ox year from Gretta
Paulina born in next Dog year from Bessie第四个输入是不必要的,因为看到第三句时,我们就可以求出Elsie和Bessie间的年龄差了。虽说题目中限定了最多有100句陈述,全部处理的时间非常短,但确实是一个可以改进的地方。
请试着修改程序,避免不必要的多余处理。
2. Comfortable Cows
Farmer John的草地可以被看作是一个由正方形方格组成的巨大的二维方阵(想象一个巨大的棋盘)。初始时,草地上是空的。
Farmer John将会逐一地将N(\(1 \le N \le 10^5\))头奶牛加入到草地上。第i头奶牛将会占据方格\((x_i,y_i)\),不同于所有已经被其他奶牛占据的方格\((0\le x_i, y_i \le 1000\))。
一头奶牛被称为是“舒适的”,如果它水平或竖直方向上与恰好三头其他奶牛相邻。Farmer John对他的农场上舒适的奶牛数量感兴趣。对1…N中的每一个 i,输出第i头奶牛加入到草地上之后舒适的奶牛的数量。
输入格式(从终端 / 标准输入读入):
输入的第一行包含一个整数N
以下N行每行包含两个空格分隔的整数,表示一头奶牛所在的方格坐标 (x,y)。输入保证所有方格的坐标是不同的。
输出格式(输出至终端 / 标准输出):
输出的第i行包含前i头奶牛加入到草地上之后舒适的奶牛的数量。
分析
这道题目的关键有两点。
第一,是要弄清楚一点:每次加入一头牛的时候,会有两个状态的切换(“加入前”和“加入后”)。牛i加入前,它的邻居(最多4个)的舒适数量可能有变化;牛i加入后,它和它的邻居的舒适数量有可能会变化。这两个数量之间的差,就是总的舒适度的变化。
第二,我们必须判定什么是“合法”的邻居,并计算邻居的数量。
搞清这两个关键后,思路也就有了:
- 设置一个二维数组,存放某个位置上是否有牛。
- 定义一个辅助函数,完成邻居判定。
- 定义一个辅助函数,完成舒适度判定。
答案

思考
这段程序用一个所谓的running count来追踪舒适数量,而不是重复地去“数”所有牛的舒适状态。这个是值得注意的。“如非必要,勿添实体”的奥卡姆剃刀原则再次得到应用。
3. Clockwise Fence
围绕Farmer John最大的草地的栅栏已经损坏了,如今他终于决定要换一个新的栅栏。
不幸的是,当Farmer John在铺设新栅栏时,一只巨大的蜜蜂突然出现,在他的草地上追着他跑,导致最后栅栏被沿着一条相当不规则的路径铺设。栅栏可以用一个字符串表示,每个字符为"N"(north,北)、"E"(east,东)、"S"(south,南)、"W"(west,西)之一。每个字符表示一米长的一段栅栏。举例来说,如果字符串为NESW,这表示栅栏从起点开始向北延伸1米,然后向东延伸1米,然后向南延伸1米,然后向西延伸1米,回到栅栏的起点。
栅栏的结束位置与开始位置相同,而这是栅栏的路径上唯一会被到达多次的位置(从而起始位置是唯一会被再次到达的位置,在栅栏结束之时)。结果,栅栏确实围起了一个草地上连通的区域,尽管这个区域可能形状十分奇特。
Farmer John 想要知道他铺设栅栏的路径是顺时针(当按字符串表示的顺序沿着栅栏的路径行走时被围起的区域位于右侧)还是逆时针(被围起的区域位于左侧)。
输入格式(从终端 / 标准输入读入):
输入的第一行包含一个整数N(\(1 \le N \le 20\))。以下N行每行包含一个长度不小于4且不超过100的字符串,表示一个栅栏的路径。
输出格式(输出至终端 / 标准输出):
对N条输入的栅栏路径的每一条,输出一行,为"CW"(clockwise,顺时针)或 "CCW"(counterclockwise,逆时针)。
输入样例:
2
NESW
WSSSEENWNEESSENNNNWWWS输出样例:
CW
CCW分析
这道题目有点绕,关键点在于如何用数学的方式表示“顺时针”和“逆时针”,以及封闭栅栏的一个特性。
我们先看数学上的定义。
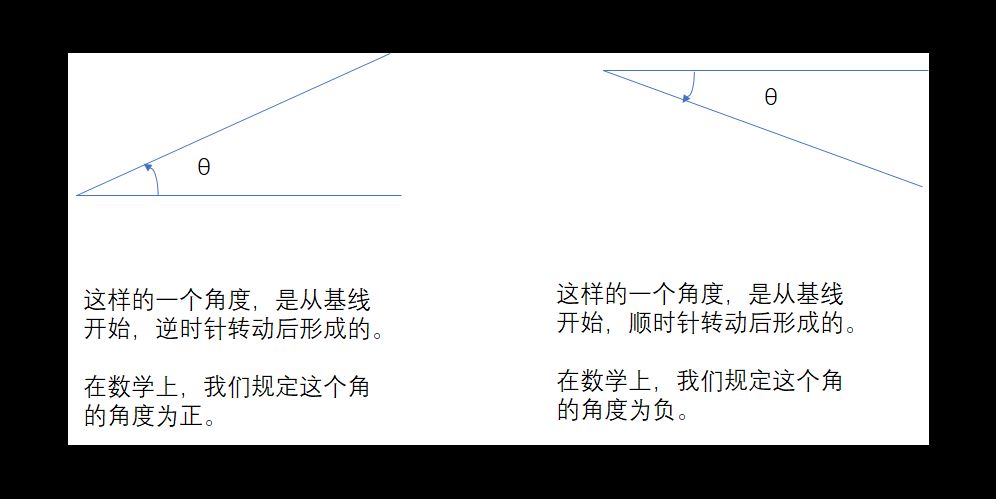
我们再看一下方向切换(不考虑反过来走,比如从E到W的切换),从E到N我们认为是逆时针的,因为和时钟的转动方向相反;从E到S是顺时针的,因为和时钟的转动方向相同。也因此,转动的角度分别是90度和-90度——顺负逆正。
一个封闭的栅栏,不管中间如何走来走去、转来转去,在过程中,它转过的角度的和,一定是360度(这是我们认为它是逆时针的),或者-360度(这是我们认为它是顺时针的)。
因此,自然地,我们需要一个辅助函数,来给出两个栅栏方向间转动的角度,并进行累计。
在实际操作中,我们不用写一串if...else...,我们可以直接给各个方向赋予一个初始的约定的角度:
E0N90W180S270
判定两个方向间的角度差,可以简化为:
- 第一个方向的角度+90度(对360求余)= 第二个方向的角度:90
- 第一个方向的角度= 第二个方向的角度:0
- 第一个方向的角度+270度(对360求余)= 第二个方向的角度:-90
- 不允许掉头:不会出现180
上述的判定也可以用一个辅助函数来实现。
答案

思考
这个程序在我的Linux机器上编译时,会有一个警告,大意是“angle_from_direction这个函数中的控制结构,没有完全“封闭”。确实如此:
int angle_from_direction(char a)
{
fi (a == 'E')
return 0;
if (a == 'N')
return 90;
if (a == 'W')
return 180;
if (a == 'S')
return 270;
}试着去掉这个警告信息吧,同时考虑用switch改写一下。