本页面已浏览75次

1. Uddered but not Herd

一个鲜为人知的事实是，奶牛拥有自己的文字：“牛文”。牛文由26个字母'a'到'z'组成，但是当奶牛说牛文时，可能与我们所熟悉的'abcdefghijklmnopqrstuvwxyz'不同，她会按某种特定的顺序排列字母。

为了打发时间，奶牛Bessie在反复哼唱牛文字母歌，而Farmer John好奇她唱了多少遍。

给定一个小写字母组成的字符串，为Farmer John听到Bessie唱的字母，计算Bessie至少唱了几遍完整的牛文字母歌，使得Farmer John能够听到给定的字符串。Farmer John 并不始终注意Bessie所唱的内容，所以他可能会漏听Bessie唱过的一些字母。给定的字符串仅包含他记得他所听到的字母。

输入格式（从终端/标准输入读入）：

输入的第一行包含 26 个小写字母 'a' 到 'z' 的牛文字母表顺序。下一行包含一个小写字母组成的字符串，为 Farmer John 听到 Bessie 唱的字母。字符串的长度不小于1且不大于 1000。

输出格式（输出至终端/标准输出）：

输出 Bessie 所唱的完整的牛文字母歌的最小次数。

输入样例：

abcdefghijklmnopqrstuvwxyz
mood

输出样例：

3

在这个样例中，牛文字母表与日常的字母表的排列一致。

Bessie 至少唱了三遍牛文字母歌。有可能 Bessie 只唱了三遍牛文字母歌，而 Farmer John 听到了以下被标记为大写的字母。

abcdefghijklMnOpqrstuvwxyz
abcdefghijklmnOpqrstuvwxyz
abcDefghijklmnopqrstuvwxyz

分析

这道题的关键在于读懂题目以及分析透样例。

如果Bessie的哼唱是abcdefghijl....xyz（我们设定该变量为alphabet），如果FJ要听到mood（我们设定该变量为s）的话，我们可以这样来推理：

1. 第一次必须但也只能听到mo。如果第一次只听到m，那么后面的两个o就需要再听两次。
2. 第二次必须但也只能听到o。d是听不到的，因为d在o的前面——换句话说，FJ在第二次的时候漏听了d。
3. 最后一次听到d，从而满足了输入的要求。

总结一下：

1. FJ第一次听Bessie哼唱，必然听到s中的第一个字母。
2. 后续字母能否听到，取决于这个字母在alphabet列表中，是否在听到的第一个字母之后。是，那么必然听到（否则就要多听一次了）；否，则必须多听一次。
3. 重复上述步骤，次数加1。

我们先看USACO提供的答案。

答案

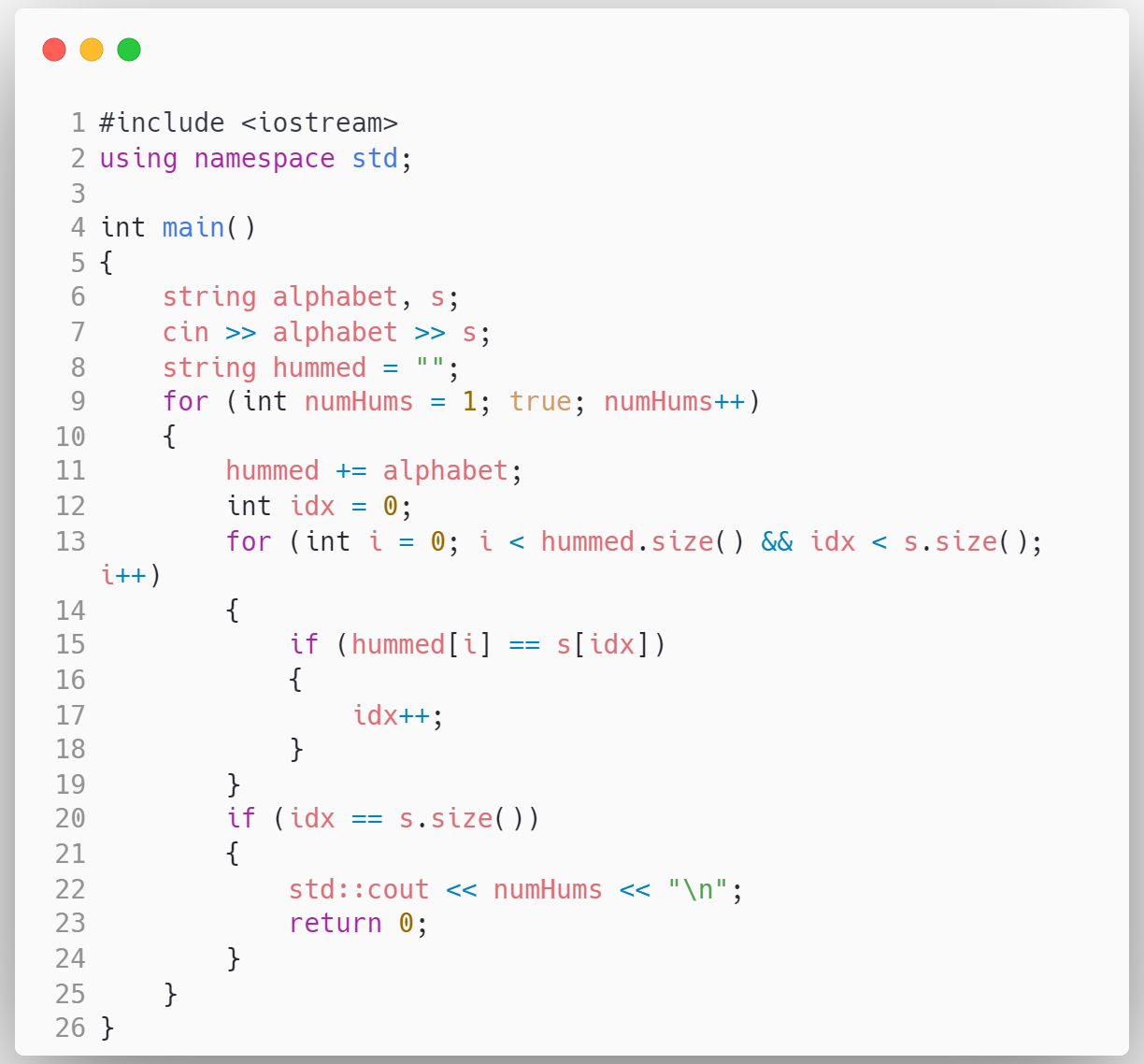
思考

请认真阅读13行-19行的for循环。这是本程序的核心部分。

这段代码中，没有用从头去找下一个字母的方式，而是通过模拟Bessie哼唱的过程进行顺序查找。也就是说，Bessie哼唱一次abcd...xyz，此时hummed=abcd...xyz；Bessie第二次哼唱时，hummed=abcd...xyzabc...xyz。

第一次搜索时，搜索的指针（i）肯定在找到的最后一个字母之后（比如找到了mo中的o之后的位置），此时在hummed=abcd...xyz中，已经找不到o了。所以，找遍hummed.size()也不会成功。于是进入第9行的循环，到11行的时候，hummed=abcd...xyzabc...xyz。这样可以继续查找下去，找到了moo中的第二个o。

请思考用别的方式（比如while循环）来实现。

2. Even More Odd Photos

Farmer John 正再一次尝试给他的N头奶牛拍照（\(2\le N \le 1000\)）。

每头奶牛有一个范围在 1…100之内的整数的“品种编号”。Farmer John对他的照片有一个十分古怪的构思：他希望将所有的奶牛分为不相交的若干组（换句话说，将每头奶牛分到恰好一组中）并将这些组排成一行，使得第一组的奶牛的品种编号之和为偶数，第二组的编号之和为奇数，以此类推，奇偶交替。

Farmer John 可以分成的最大组数是多少？

输入格式（从终端/标准输入读入）：

输入的第一行包含N。下一行包含N个空格分隔的整数，为N头奶牛的品种编号。

输出格式（输出至终端/标准输出）：

输出 Farmer John 的照片中的最大组数。可以证明，至少存在一种符合要求的分组方案。

输入样例：

7
1 3 5 7 9 11 13

输出样例：

3

在这个样例中，以下是一种分成最大组数三组的方案。将1和3分在第一组，5、7和9分在第二组，11和13分在第三组。

输入样例：

7
11 2 17 13 1 15 3

输出样例：

5

在这个样例中，以下是一种分成最大组数五组的方案。将2分在第一组，11分在第二组，13和1分在第三组，15分在第四组，17和3分在第五组。

分析

最自然的想法是啥？

如果给出的N个数，“正好”是一半偶数，一半奇数，或者偶数数量（E）比奇数数量（O）多一个，就能完美地排出“偶-奇-偶-奇-……-奇(-偶)”的队形。

所以，我们得到了一个重要的结论：要想得到最多的分组，\(E=O\)，或者\(E=O+1\)。

考虑其他情况：

1. 如果\(E \gt O+1\)，我们的偶数太多了。
   1. 我们先这么做：一头偶数牛，一头奇数牛，一头偶数牛，一头奇数牛……这样的操作可以执行O次。
   2. 剩下的全都是偶数牛。将所有这些偶数牛归到一组。由于“偶数+偶数=偶数”，所以最后一组还是偶数，符合要求。
   3. 这时，总的分组数是\(2O+1\)。
2. 如果\(E\lt O\)，我们的奇数多了。考虑到：“奇数+奇数=偶数”，所以我们可以用两个奇数来变成一个偶数，直到归并到上述1的情形。

想清楚这个后，代码就比较简单了。

答案

思考

可以进一步考虑如果排列规则改为“奇-偶-奇”这样，对我们的算法有什么影响？

3. Just Stalling

Farmer John有N头奶牛（\(1 \le N \le 20\)），高度为\(a_1, a_2, ... a_N\)。他的牛栏有N个牛棚，高度限制分别为\(b_1, b_2, ... b_N\)（例如，如果\(b_5=17\)，那么一头高度不超过17的奶牛可以住在牛棚5里）。Farmer John有多少种不同的方式安排他的奶牛，使得每头奶牛均住在不同的牛棚里，并且使得每个牛棚的高度限制均得到满足？

输入格式（从终端/标准输入读入）：

输入的第一行包含N

第二行包含N个空格分隔的整数\(a_1, a_2, ... a_N\)

第三行包含N个空格分隔的整数\(b_1, b_2, ... b_N\)

所有的高度和高度限制均在范围 \([1,10^9]\)内。

输出格式（输出至终端/标准输出）：

输出Farmer John可以将每头奶牛安排到不同的牛棚里，使得每个牛棚的高度限制均得到满足的方法数。注意输出的数量可能需要使用64位整数型，例如C++中的long long。

输入样例：

4
1 2 3 4
2 4 3 4

输出样例：

8

在这个例子中，我们不能将第三头奶牛安排到第一个牛棚里，因为\(3=a_3 \gt b_1=2\)。类似地，我们不能将第四头奶牛安排到第一或第三个牛棚里。一种符合高度限制的安排方式为将奶牛1安排到牛棚1，奶牛2 安排到牛棚2，奶牛3安排到牛棚3，奶牛4安排到牛棚4。

分析

这道题可以选择用暴力法求解，但随着牛的数量增加，暴力法会严重超时。

我们可以将其看成带限制条件的排列。

最高的牛收到限制最大，它只能进入比较高的牛棚。因此，我们可以将牛按照从高到低排序，然后依次处理：

1. 第一高的牛能进入的牛棚数量，是大于等于它高度的牛棚的数量。
2. 第二高的牛能进入的牛棚数量，是大于等于它高度的牛棚的数量，减去1（因为已经被占了一个）。
3. 第三高的牛能进入的牛棚数量，是大于等于它高度的牛棚的数量，减去2（因为已经被占了两个）。
4. ……

以此类推。因此，最后的总的方案数量，是上述各个数量的乘积。

答案

思考

这道题提示我们，算法才是关键！