本页面已浏览83次

1. Acowdemia I

由于对计算机科学的热爱，以及有朝一日成为“Bessie博士”的诱惑，奶牛Bessie开始攻读计算机科学博士学位。经过一段时间的学术研究，她已经发表了N篇论文（\(1 \le N \le 10^5\)），并且她的第i篇论文得到了来自其他研究文献的\(c_i\)次引用（\(0 \le c_i \le 10^5\)）。

Bessie听说学术成就可以用h指数来衡量。h指数等于使得研究员有至少h篇引用次数不少于h的论文的最大整数h。例如，如果一名研究员有4篇论文，引用次数分别为 (1, 100, 2, 3)，则h指数为2，然而若引用次数为 (1, 100, 3, 3) 则h 指数将会是3。

为了提升她的h指数，Bessie计划写一篇综述，并引用一些她曾经写过的论文。由于页数限制，她至多可以在这篇综述中引用L篇论文（\(0 \le L \le 10^5\)），并且她只能引用每篇她的论文至多一次。

请帮助Bessie求出在写完这篇综述后她可以达到的最大h指数。

注意Bessie的导师可能会告知她纯粹为了提升h指数而写综述存在违反学术道德的嫌疑；我们不建议其他学者模仿Bessie的行为。

输入格式（从终端 / 标准输入读入）：

输入的第一行包含N和L。

第二行包含N个空格分隔的整数\(c_1, …, c_N\)。

输出格式（输出至终端 / 标准输出）：

输出写完综述后Bessie可以达到的最大h指数。

输入样例：

4 0
1 100 2 3

输出样例：

2

Bessie 不能引用任何她曾经写过的论文。上文中提到，(1, 100, 2, 3)的h指数为2。

输入样例：

4 1
1 100 2 3

输出样例：

3

如果 Bessie 引用她的第三篇论文，引用数会变为 (1, 100, 3, 3)。上文中提到，这一引用数的h指数为3。

分析

我们从最简单的情形开始。

如果L=0（Bessie不能引用任何她的论文），那么h值很容易找到：

1. 将论文引用数从高到低排列。\((1, 100, 2, 3)\Rightarrow (100, 3, 2, 1)\)。
2. 从头开始遍历：
   1. \(h=1，c_i=100\)，可以继续。
   2. \(h=2，c_i=3\)，可以继续。
   3. \(h=3，c_i=2\)，不能继续。
3. 因此，在这种情况下，h最大只能是2。

现在考虑L>0的情形。由于不能引用同一篇文章多次，所以我们可以证明：h最多加1。为什么？因为，第h+1篇论文在“操作”之前，最多有h次引用，它就算再被引用一次，它的引用次数也不会超过h+1。

但不是所有情形下，h会加1。

在操作前，有h篇文章的引用数至少是h，而其中有k篇文章的引用次数正好是h（因此其他排名更靠前的论文的引用次数大于h）。要想将h提升1，这k篇文章必须被引用1次，而且第h+1篇文章也要被引用1次。所以，务必使得\(L\ge k+1\)，但是如果第h+1篇文章引用次数小于h，我们也无法增加h指数——它必须正好等于h，才能最终达到h+1。

有了这个思路，我们来看解法。

答案

思考

这套题不算特别难，只要分析清楚，就能比较顺利地写出代码并完成。

2. Acowdemia II

Bessie正在申请计算机科学的研究生，并取得了一所久负盛名的计算机科学实验室的面试通知。然而，为了避免冒犯任何人，Bessie有意先确定实验室的N名现有成员的相对资历（\(1 \le N \le 100\)）。没有两名实验室成员的资历相同，但确定他们的资历深浅可能并不好办。为此，Bessie将会对实验室的出版物进行调查。

每份出版物均包含一个作者列表，为所有N名实验室成员的一个排列。列表按每名实验室成员对这篇文章的贡献降序排列。如果多名研究员的贡献相等，则按字典序排列。由于更有资历的实验室成员负有更多的管理责任，更有资历的研究员从不会比资历较浅的研究员做出更多的贡献。

例如，在一个由资历较浅的学生Elsie、资历较深的教授Mildred、以及十分资深的教授Dean组成的实验室中，可能存在一篇论文Elsie-Mildred-Dean，如果他们做出了不等的贡献（也就是说，Elsie 做出的贡献比 Mildred 更多，Mildred 比 Dean 更多）。然而，也有可能存在一篇论文Elsie-Dean-Mildred，如果Mildred和Dean做出了相等的贡献，而Elsie做出了更多的贡献。

给定实验室的K份出版物（\(1\le K \le 100\)），对于实验室中每对研究员，如果可能的话帮助Bessie判断其中谁的资历更深。

输入格式（从终端 / 标准输入读入）：

输入的第一行包含两个整数K和N。

第二行包含N个空格分隔的字符串，为实验室的成员的名字。每个字符串均由小写字母组成，且至多包含10个字符。

以下K行，每行包含N个空格分隔的字符串，表示一份出版物的作者列表。

输出格式（输出至终端 / 标准输出）：

输出N行，每行N个字符。在第i行内，对于所有\(j\ne i\)，当可以确定第i名成员比第j名成员资历更深时字符j为1，当可以确定第i名成员比第j名成员资历更浅时字符j为0，当不能由给定的出版物确定时为?。

第i行的字符i应为B，因为这是Bessie最喜欢的字母。

输入样例：

1 3
dean elsie mildred
elsie mildred dean

输出样例：

B11
0B?
0?B

在这个样例中，单独一份论文elsie-mildred-dean并不能提供足够的信息判断Elsie比Mildred资历更深或更浅。然而，我们可以推断出Dean一定比这两名研究员资历更深，从而资历排序为\(Elsie\lt Mildred \lt Dean\)和\(Mildred\lt Elsie \lt Dean\)均是可能的。

输入样例：

2 3
elsie mildred dean
elsie mildred dean
elsie dean mildred

输出样例：

B00
1B0
11B

在这个样例中，唯一能与两篇论文相一致的资历排序为\(Elsie\lt Mildred\lt Dean\)，这是因为基于第一个样例所提供的信息，第二篇论文可以帮助我们推断出Mildred比Elsie的资历更深。

分析

我们从最简单的情形出发。假定只有一篇论文（K=1），而作者列表是\(n_1, n_2, n_3, ..., n_N\)。我们怎么判定作者的资深度？

按照题设，很显然的是，如果\(n_i\lt n_{i+1}\lt ... \lt n_N\)（也就是从i开始，所有的人名都是按序排列的），那么我们无法判定这几个人的资深度——他们贡献了相同的贡献度。

但是，如果对于某个i和i+1，出现了\(n_i \gt n_{i+1}\)这样的反常现象，那么显然的情况就是，\(n_1, n_2, ..., n_i\)这些人都做出了更大的贡献，也因此这些人的资深度不如\(n_{i+1}\)之后的人。

这个过程是可以重复的、叠加的。所以，如果有多本出版物（K>1），我们重复上述的过程就能逐步判定了。

答案

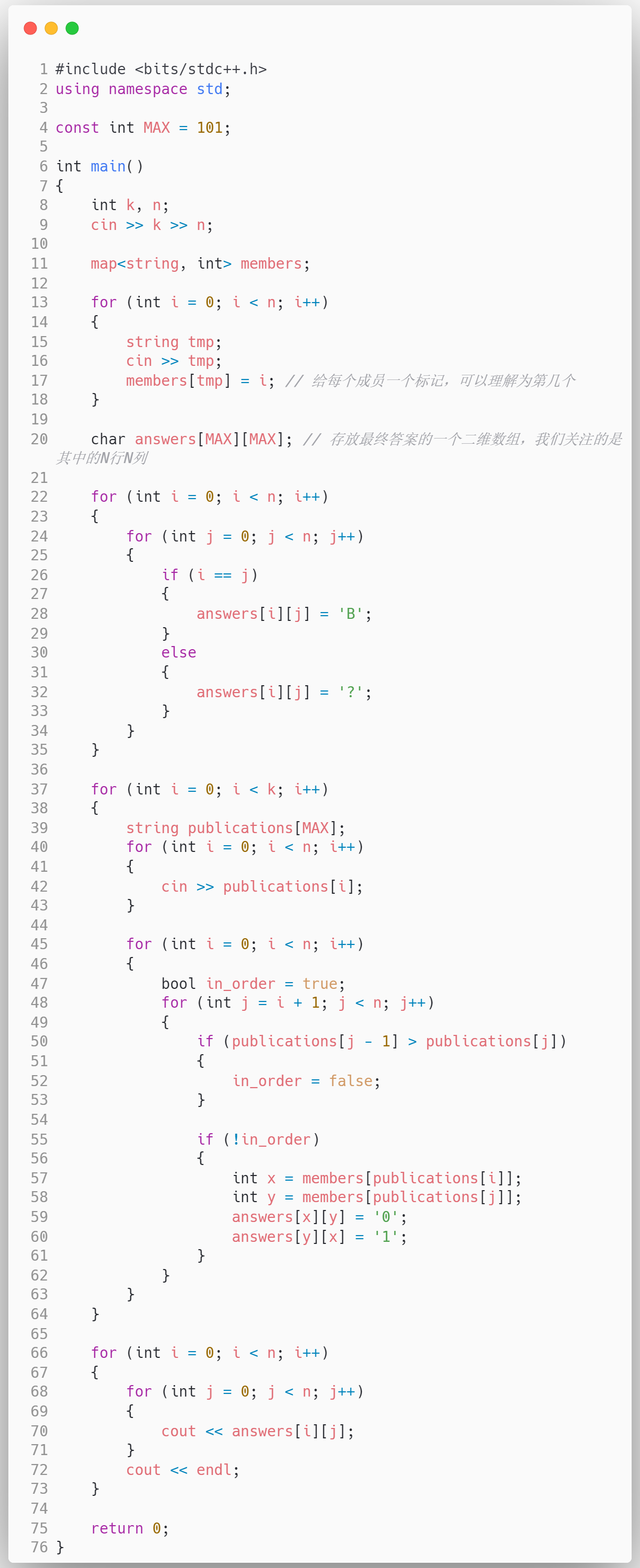
思考

这是一道很有趣的题目。关键点是找到分析中提到的规律。总体而言，还是一个从最简单状态出发、逐渐推广的路子。

3. Acowdemia III

Bessie是一位忙碌的计算机科学研究生。然而，即使是研究生也需要交友。因此，Farmer John开设了一片草地，目的是为了帮助 Bessie 与其他奶牛建立持久的友谊。

Farmer John的草地可以被看做是由正方形方格组成的巨大二维方阵（想象一个巨大的棋盘）。每个方格用如下字符标记：

• C，如果这个方格中有一头奶牛。
• G，如果这个方格中有草。
• .，如果这个方格既没有奶牛也没有草。

对于两头想要成为朋友的奶牛，她们必须选择在一个与她们要么水平要么竖直方向上均相邻的有草方格见面。在这个过程中，她们会在这个有草方格中吃草，所以之后的奶牛不能再使用这个方格作为见面地点。一头奶牛可以与多头其他奶牛成为朋友，但是同一对奶牛不能见面并成为朋友多于一次。

Farmer John希望有许多奶牛可以见面并成为朋友。请求出当这一活动结束时在奶牛之间可以建立的朋友关系的最大数量。

输入格式（从终端 / 标准输入读入）：

输入的第一行包含N和M（\(1\le N, M\le 1000\)）。

以下N行每行包含一个由M个字符组成的字符串，表示这个草地。

输出格式（输出至终端 / 标准输出）：

输出在这一活动结束时在奶牛之间可以建立的朋友关系的最大数量。

输入样例：

4 5
.CGGC
.CGCG
CGCG.
.CC.C

输出样例：

4

如果我们用坐标 (i,j) 标记第i行第j列的奶牛，则在这个样例中于(1,2)、(1,5)、(2,2)、(2,4)、(3,1)、(3,3)、(4,2)、(4,3) 以及 (4,5) 存在奶牛。一种使四对奶牛成为朋友的方式如下：

• 位于 (2,2) 和 (3,3) 的奶牛于 (3,2) 一起吃草。
• 位于 (2,2) 和 (2,4) 的奶牛于 (2,3) 一起吃草。
• 位于 (2,4) 和 (3,3) 的奶牛于 (3,4) 一起吃草。
• 位于 (2,4) 和 (1,5) 的奶牛于 (2,5) 一起吃草。

分析

虽然题目中是牛在移动并试着找朋友，但找到朋友的前提是有一块有草的草地。

而所谓“要么水平要么竖直方向上均相邻的有草方格”，是什么意思呢？我们以上面的样本输入来画一张图：

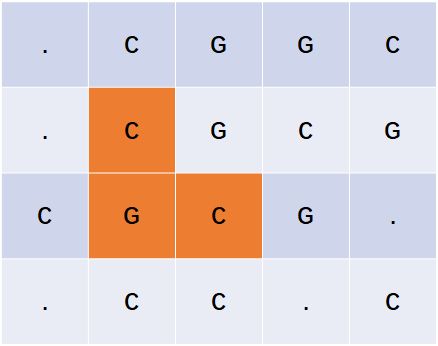
位于(2,2)和(3,3)的两头奶牛，可以在(3,2)那里吃草。所以，一种思考角度，是(i, j)和(k,l)必须先满足以下条件：

1. 要么在一行上，此时\(|i-k|=2\)；或者在一列上，此时\(|j-l|=2\)。
2. 要么就是“斜对角”，此时\(|i-k|=1 \cap |j-l|=1\)。

因此判定的思路就差不多好了：

首先，如果(x, y)这个地方是草：

1. 如果左边(x-1, y)而且右边(x+1, y)是牛；或者上边(x, y+1)而且下边(x, y-1)是牛，那么配对成功，计数加1，另外(x, y)这个地方要变成“无”。
2. 这里我们先解决同一行/同一列的牛交到朋友的情况。后续的判定时，不用再考虑这个情况。

其次，如果(x, y)这个地方是牛：

注意到，在上一步的时候，我们已经处理完所有同行/同列的情形，这里不用再考虑。

再注意到，两头处在“对角”的牛的位置的对称性：一种是两牛在1/3象限对角，一种是两牛在2/4象限对角。我们只用判断这两种情形即可。而对于每种对角位置，草的位置也有两种，我们需要分别判断，所以总共是四个判断。如图所示（我们用绿色表示草，棕色表示牛）：

当然啦，两头牛碰头的地方的草地要标记为“无”。

另外，我们必须处理边界上的牛或者草，为了避免繁冗的边界判定，我们可以在原来的n*m大小的草地“周边”加一圈“空草地”（既没有草也没有牛）。这么做不会影响结果，但可以避免边界判定。

答案

分析

提醒一点，在二维数组的处理中，我们的书写习惯是从左到右（增加了列数）、从上到下（增加了行数）；而常规的平面直角坐标系中，x轴反而更像是列，y轴反而像行（但递增方向和二维数组相反）。

在我的处理中，我用了坐标系的约定，而不是常规的行列约定。这不会影响本题的结果。

本题的难点在于，确定相遇的条件。我在处理时，分别采用了从草地出发和从某一头牛出发的处理。有兴趣的读者，可以改写一下，改为都从草地出发或者牛出发，应该可以获得相同的结果。

另外，USACO真题的好处在于，它提供了测试数据，可以用来验证程序的正确性。以本题为例，它一共提供了12个测试数据（含输入和输出）。输入数据量从测试1中的\(4*5\)个到测试12的\(1000*1000\)个。

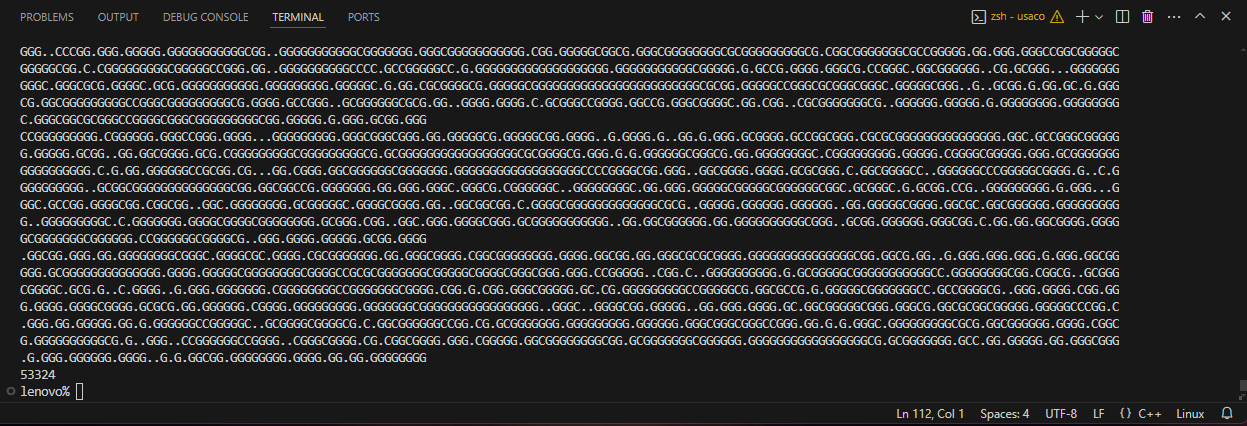
对于大型数据输入，比较好的方式是用文件进行读写：读入一个.in数据（输入数据），进行处理，得到答案并和对应的.out数据进行比较。如果12个测试数据都能通过，那么程序就可以获得满分。

这里，我们不讨论文件的操作，但希望要进行USACO竞赛的同学，必须掌握。