本页面已浏览82次

1. Lonely Photo

Farmer John最近购入了N头新的奶牛（\(3\le N\le 5×10^5\)），每头奶牛的品种是更赛牛（Guernsey）或荷斯坦牛（Holstein）之一。

奶牛目前排成一排，Farmer John想要为每个连续不少于三头奶牛的序列拍摄一张照片。 然而，他不想拍摄这样的照片，其中只有一头牛的品种是更赛牛，或者只有一头牛的品种是荷斯坦牛——他认为这头奇特的牛会感到孤立和不自然。在为每个连续不少于三头奶牛的序列拍摄了一张照片后，他把所有「孤独的」照片，即其中只有一头更赛牛或荷斯坦奶牛的照片，都扔掉了。

给定奶牛的排列方式，请帮助Farmer John求出他会扔掉多少张孤独的照片。如果两张照片以不同的奶牛开始或结束，则认为它们是不同的。

输入格式（从终端 / 标准输入读入）：

输入的第一行包含N。

输入的第二行包含一个长为N的字符串。如果队伍中的第i头奶牛是更赛牛，则字符串的第i个字符为G。否则，第i头奶牛是荷斯坦牛，该字符为H。

输出格式（输出至终端 / 标准输出）：

输出Farmer John会扔掉的孤独的照片数量。

输入样例：

5
GHGHG

输出样例：

3

这个例子中的每一个长为3的子串均恰好包含一头更赛牛或荷斯坦牛——所以这些子串表示孤独的照片，并会被Farmer John扔掉。所有更长的子串（GHGH、HGHG 和 GHGHG）都可以被接受。

分析

这道题的要求很简单，解析成数学语言就是：对于一个长度\(\ge 3\)的字符串，判定是不是只有一个G或者只有一个H。

最直接的解法，是按照这个思路去一个一个检查。符合条件的字符串有\(N^2\)个，而每次检查需要遍历子串（\(O(N)\)）。因此，最终的时间复杂度来到了\(O(N^3)\)。

一个改进的方式，可以让时间复杂度降到\(O(N^2)\)：我们每次固定子串中最左边的字符，然后一个一个向右找。如果我们找了至少3个字符，而且其中只有一个G或者一个H，那这张照片就是要被扔掉的（计数加1）。我们一个一个地改变最左边字符（向右走），最后就能得到结果。

答案

思考

相比USACO给出的答案，我们进行了一次优化（39-42行）：如果G和H的数量都\(\ge 2\)，那么可以保证的是：没有哪种牛是“孤单”的，而且照片中的牛的数量一定超过了3。后续不论如何，这些照片都不会被删除，因此我们可以跳出内循环了。这样虽然没能降低时间复杂度，但至少可以优化一部分。这样的小修补，也是一种成就。

还有没有更省时间的方式？

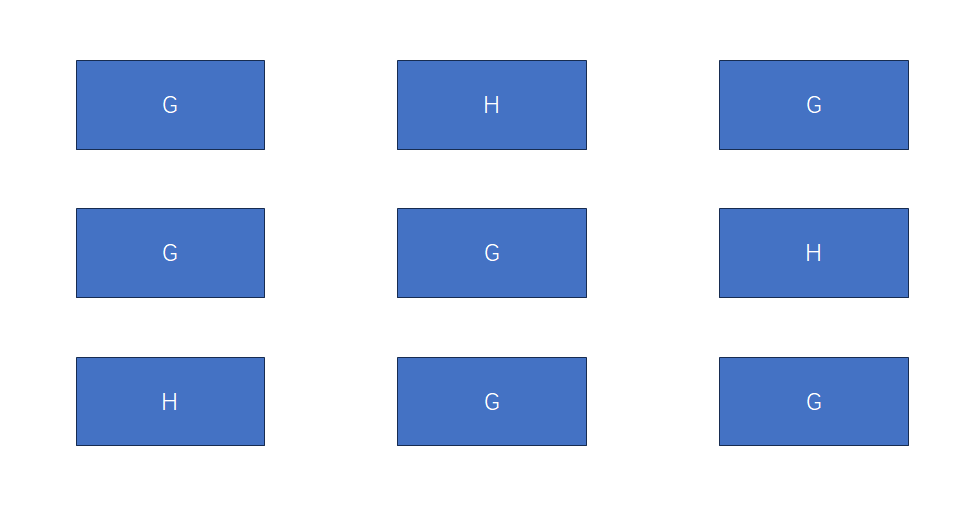
我们来看下所谓“孤独”的牛出现时，是怎样的情况。先从3头牛开始，下图中，H牛是孤独的：

再扩展到多头牛的情况：

...	G	G	G	H	G	G	G	G	...

中间的这头H牛（假定是s[i]）显然很“孤独”。

1. 往左看，s[i-1]!=s[i]，所以左计数（lhs）要加1。
2. 在这个情况下，k从i-2开始往左，所有的s[k]==s[i-1]，lhs加1。
3. 1-2完成的工作是：就当前的s[i]，向左计算与s[i]不同的字符s[i-1]的最大连续长度。
4. 最终得到的lhs是这个长度。

向右看的情形类似。这两个过程结束后，我们分别得到了lhs和rhs。考虑不同的组合的情况（还是以上图为例，孤独的牛是H）：

1. 左右都是G：则左边有lhs头G，右边有rhs头G，这样的组合有\(lhs*rhs\)种。
2. G都在左边而不在右边：那么最多有lhs-1种。
3. G都在右边而不再左边：那么最多有rhs-1种。

注意，2/3两种情况要考虑lhs和rhs是1的情况，这时是不构成单边“孤独”的情形的。

最后的代码如下，请大家注意循环的终止和各自情形下的判定。

USACO声称，这个算法的复杂度是\(O(N)\)。但我们似乎看到了两个循环，这是怎么回事？

我请教了ChatGPT-4o，它一开始也认为是\(O(N^2)\)的复杂度，经过进一步提示后，它的分析如下。

==============

即使一个字符串只包含'H'和'G'，我们对于每个字符只检查它的“紧邻”，而且这是一个线性扫描收敛于\(O(N)\)。

===============

这给了我们一个重要的提示：不是光看for循环就能确定时间复杂度的，在这个例子中，最终的复杂度还是收敛到了\(O(N)\)。

2. Air Cownditioning

Farmer John的N头奶牛对他们牛棚的室温非常挑剔。有些奶牛喜欢温度低一些，而有些奶牛则喜欢温度高一些。

Farmer John的牛棚包含一排N个牛栏，编号为\(1...N\)，每个牛栏里有一头牛。 第i头奶牛希望她的牛栏中的温度是\(p_i\)，而现在她的牛栏中的温度是\(t_i\)。为了确保每头奶牛都感到舒适，Farmer John安装了一个新的空调系统。该系统进行控制的方式非常有趣，他可以向系统发送命令，告诉它将一组连续的牛栏内的温度升高或降低1个单位——例如“将牛栏5…8的温度升高1个单位”。一组连续的牛栏最短可以仅包含一个牛栏。

请帮助 Farmer John求出他需要向新的空调系统发送的命令的最小数量，使得每头奶牛的牛栏都处于其中的奶牛的理想温度。

输入格式（从终端 / 标准输入读入）：

输入的第一行包含N。下一行包含N个非负整数\(p_1...p_N\)，用空格分隔。最后一行包含N个非负整数\(t_1...t_N\)。

输出格式（输出至终端 / 标准输出）：

输出一个整数，为Farmer John需要使用的最小指令数量。

输入样例：

5
1 5 3 3 4
1 2 2 2 1

输出样例：

5

一组最优的 Farmer John 可以使用的指令如下：

初始温度 ：1 2 2 2 1

升高牛棚 2..5：1 3 3 3 2

升高牛棚 2..5：1 4 4 4 3

升高牛棚 2..5：1 5 5 5 4

降低牛棚 3..4：1 5 4 4 4

降低牛棚 3..4：1 5 3 3 4

分析

这道题一共有两种解法。我们一个一个地分析。

作为一个预备工作，我们创建另外一个数组d，用来存放每一头当前牛棚温度和理想温度的差（\(p_i-t_i\)）。我们的目的当然是所有d里的元素都是0。

注意，我们对一个区间的牛棚调整一次（温度变化1）的时候，所有的d也会被调整一次。

直觉

首先是最直观的方法。

直觉告诉我们，要想调整次数最小，有一些原则：d为0的时候，我们不调整；d是正/负的时候，我们也不去升高/降低温度。

问题进一步简化到：对于某个特定的d[N]，那么我们要找到最小的一个j使得\([j, N]\)之间的所有的d和这个特定的d[N]同号。然后进行一次调整（计数加1）。

这个动作可以执行很多次，直到d[N]为零。那么我们进入下一个牛棚，并重复上述操作。

答案

一些改进

上述这个方案的复杂度是\(P(NV)\)，其中的V是d中可能的最大值。根据题目，“温度值不超过10,000”，牛不超过100,000。这个数据量还是很大的。我们需要优化。

一个不改变复杂度的方法是，我们不用每次计算的时候，都只有1度。我们可以直接计算要调几度——这不是FJ的机器能做到的，但我们在模拟的时候可以这么做。

整体思路是：

1. 按照上面的思路，找出一串最长的d，满足：这些d不为0，而且和d[N]同号。
2. 找出这些d中的最小值，这就是要调整的度数（也就是次数）。

这个做法不能降低复杂度，但可以显著降低计算量。

改进的答案

深度分析

让我们深入分析，将复杂度降低到\(O(N)\)！

我们已经得到了数组d，并用它记录一个差值：当前温度和理想温度的差。这个差值决定了调整的次数。

我们再来分析一下d。对于d[i]和d[i+1]，如果它们相等，意味着如果我们对d[i]做任何操作，都必须对d[i+1]也做一次。这样可以更快地让d[i]和d[i+1]同时归零。而如果两者差距极大，意味着，对d[i]或者d[i+1]之一（但不是两者）至少需要做abs(d[i]-d[i+1])次操作。

我们令e[i]=abs(d[i+1]-d[i])，我们还可以观察到如下事实：

也就是对于[i, j]这个范围中的d做了一次调整后，只有e[i-1]和e[j]变化了1（总共变化了2）。当中的e值没有变。

所以，最少的次数可以用公式快速获得：\(\sum_{i=0}^N e_i/2\)

也就是数组e的和的一半。

于是，编程反而简单了。

终极答案

思考

一个模拟题，变成了数学公式！这不是“差分”唯一出现的场合。

在网上搜索“差分在编程中的应用”，可以找到很多有用的资料。比如这一篇。我摘录部分内容如下。

请特别注意上面的“将时间复杂度降低到O(1)”。这就是我们使用差分解题的出发点和得到的好处。

差分可以用物理概念来映射：

有兴趣的同学可以去阅读这篇文章。

3. Walking Home

奶牛Bessie正准备从她最喜爱的草地回到她的牛棚。

农场位于一个\(N×N\) 的方阵上（\(2\le N\le 50\)），其中她的草地在左上角，牛棚在右下角。Bessie 想要尽快回家，所以她只会向下或向右走。有些地方有草堆（haybale），Bessie无法穿过；她必须绕过它们。

Bessie今天感到有些疲倦，所以她希望改变她的行走方向至多K次（\(1\le K\le 3\)）。

Bessie有多少条不同的从她最爱的草地回到牛棚的路线？如果一条路线中Bessie经过了某个方格而另一条路线中没有，则认为这两条路线不同。

输入格式（从终端 / 标准输入读入）：

每个测试用例的输入包含T个子测试用例，每个子测试用例描述了一个不同的农场，并且必须全部回答正确才能通过整个测试用例。输入的第一行包含T（\(1\le T\le 50\)）。每一个子测试用例如下。

每个子测试用例的第一行包含N和K。

以下N行每行包含一个长为N的字符串。每个字符为.，如果这一格是空的，或H，如果这一格中有草堆。输入保证农场的左上角和右下角没有草堆。

输出格式（输出至终端 / 标准输出）：

输出T行，第i行包含在第i个子测试用例中Bessie可以选择的不同的路线数量。

输入样例：

7
3 1
...
...
...
3 2
...
...
...
3 3
...
...
...
3 3
...
.H.
...
3 2
.HH
HHH
HH.
3 3
.H.
H..
...
4 3
...H
.H..
....
H...

输出样例：

2
4
6
2
0
0
6

分析

样例给出了很好的提示：我们应该从简单（\(K=1\)）到复杂（\(K=3\)）地处理这个问题。

\(K=1\)

如果Bessie只想转一次弯就到家，只有一种可能：从左上角开始，要么它向右走到底，然后向下走到底到家（右下角）；或者，它向下走到底，然后向右走到底到家。如图：

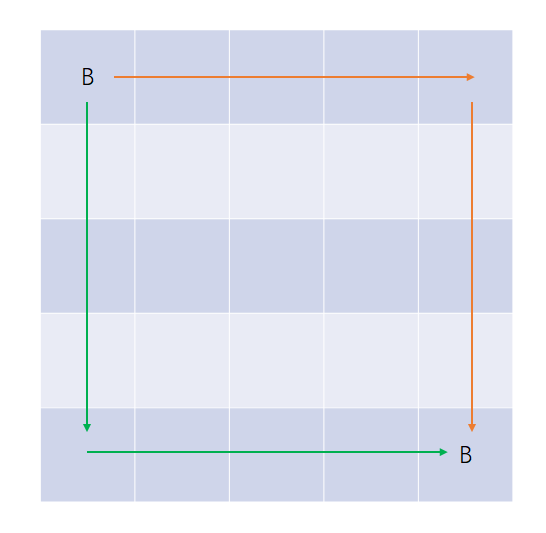
如果这两个路径上有任何格子是H，那么就走不通。否则走法加1。所以，问题归并为判定第一行、第一列、最后一行、最后一列上格子的状态。

for (int i = 0; i < n; i++)
{
    if (g[0][i] == 'H' || g[i][n - 1] == 'H') //第一行和最后一列
    {
        urcorner = false;
    }
    if (g[i][0] == 'H' || g[n - 1][i] == 'H') //第一列和最后一行
    {
        dlcorner = false;
    }
}

\(K=2\)

首先，要考虑\(K=1\)的情况，因为只转一次弯的路径是符合\(K=2\)的约束的。

如果转两次弯，会是怎样的路径呢？

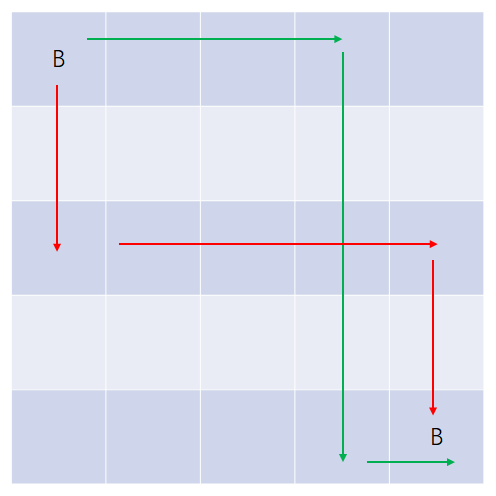
Bessie也只有两种走法：

1. 第一行向右走 -> 到某列下行一直到底 -> 右行到家。
2. 第一行向下走 -> 到某行右行一直到边 -> 下行到家。

这就是对每一列（第一种走法）或者每一行（第二种走法）进行搜索和判定的过程。

以“右下右”（上图中的绿线）的走法为例：

1. 列数（j）从第二列到最后第二列：
   1. 对于每一行（i），进行判定：
      1. 如果g[i][j]是草堆：不行；
      2. 如果本列左边的第一行有草堆：不行；
      3. 如果本列右边的最后一行有草堆：不行。
      4. 否则，可以走通。
2. 重复1的动作。

图中另外一种走法（红线，“下右下”）的分析请自行完成。

\(K=3\)

首先，要考虑\(K=1\)和\(K=2\)的情况。

Bessie转三次向的走法如下图所示：

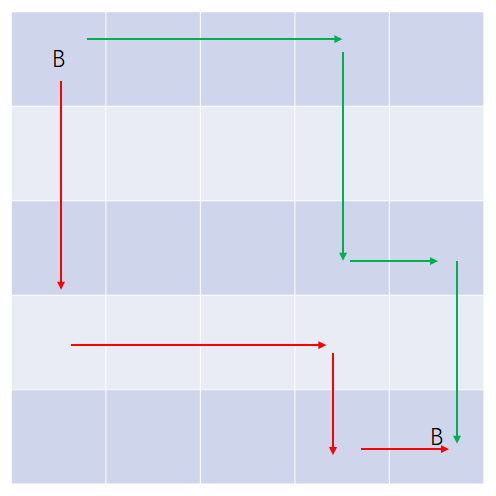
换句话说，也就是Bessie在中途要多转一次弯。我们对此可以进行与\(K=2\)时类似但扩展的判定。以“右下右下”（上图中绿线）的走法为例：

1. 对于任意一个点(i, j)，除了判定本身是否是草堆外，需要判定四个方向的草堆情况：
   1. 本列以左在第一行有草堆：不行。
   2. 本行以上在本列有草堆：不行。
   3. 本列以右在本行有草堆：不行。
   4. 本行以下在最后一列有草堆：不行。

“下右下右”（红线）走法分析类似，请自行完成。

答案

思考

这个题目难度还是适中的。同时，解法的复杂度是\(O(N^3)\)：搜索路径是一个\(O(N^2)\)的过程，而每个路径都要进行格子的判定（\(O(N)\)）。