题目
分析
作为数学入门知识,我们先讲有关模运算的一个规则:
\((a\times b) \mod c= ((a\mod c) \times (b \mod c)) \mod c\)
之所以先求模再相乘,是因为在此类题目中,如果先将一系列数字相乘,有可能中间结果会溢出。而每次先求模再相乘然后再求模,可以保证任何时候中间结果都不会溢出。
代码很简单,其核心是:如果A换算为1,那么换算公式就是:c-'A'+1。
int calculateProduct(const string& s)
{
int product = 1;
for (char c : s)
{
product = (product * (c - 'A' + 1)) % 47;
}
return product;
}输入两个字符串后,分别调用这个函数,然后比较返回值就可以了。
示例
输入两个字符串 "ABC" 和 "DEF":
-
"ABC":
- A → 1, B → 2, C → 3
- 积: \(1 \times 2 \times 3 = 6\)
- \(6 \mod 47 = 6\)
-
"DEF":
- D → 4, E → 5, F → 6
- 积: \(4 \times 5 \times 6 = 120\)
- \(120 \mod 47 = 26\)
-
比较: \(6 \neq 26\) → 输出 "STAY"
答案
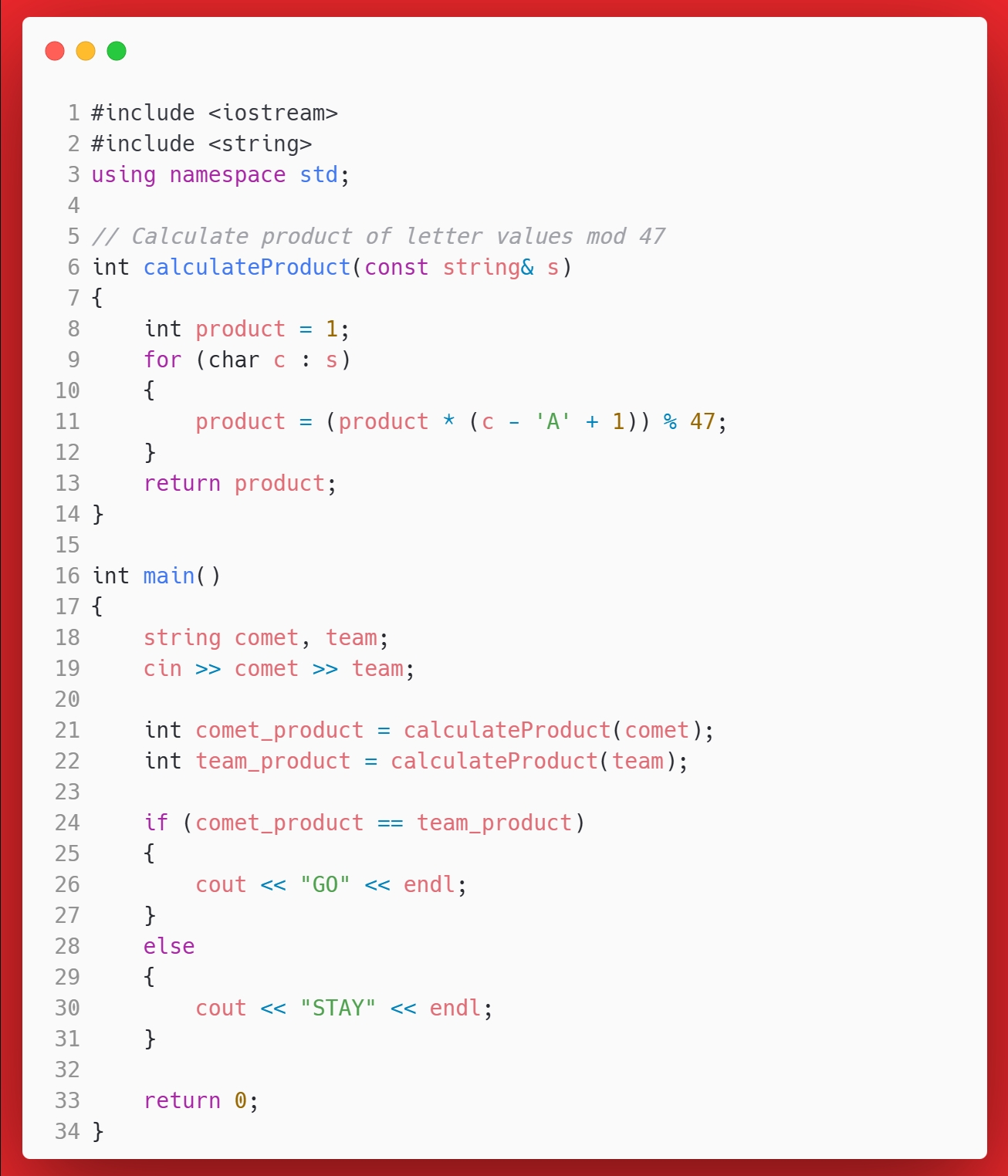
思考
本题规定字符串最长只有6个,如果都是Z,结果最大就是\(26^6=308,915,776\),远远低于int的上限,所以先算出最终乘积再求模也是没问题的。但本题的解法是更通用的,建议使用。