题目
分析
根据题意,我们知道:要对每个数字进行“是不是质数”的判定——这种重复性的类似操作,就是使用“函数”的强烈提示。
一般C++竞赛(包括编程)中,涉及到质数的算法无非是两种。一种是基于筛法的、用于一次性找到多个质数的方法;一种多用来判定一个或者几个给定的数字是不是质数。本题用的是第二种。
第二种判定方法用到的是质数的数学定义:一个正整数,如果只有1和本身是它的因子,那么就是质数。特别规定,1不是质数。
因此,我们可以用一个从2开始到n-1的循环,每次进行n%i的操作,如果能整除,那么i就是n的因子,也因此n不可能是质数。此时,我们可以提前终止循环,而选择下一个数。
在实际算法中,我们还可以进一步降低循环的上限。如果n是一个合数,那么一定存在n=p*q,而p和q中较小的那个,一定不会超过\(\sqrt n\)。所以,我们可以将循环上限限定为小于等于\(\sqrt n\),或者限定为\(i\times i\le n\)。
bool is_prime(int n)
{
if (n < 2)
{
return false;
}
for (int i = 2; i *i <=n; i++)
{
if (n % i == 0)
{
return false;
}
}
return true;
}注意,return true是在循环体外:只有当for(...)循环中,没有触发任何一次if(n % i ==0)的条件,才能保证这个数不是合数。
答案
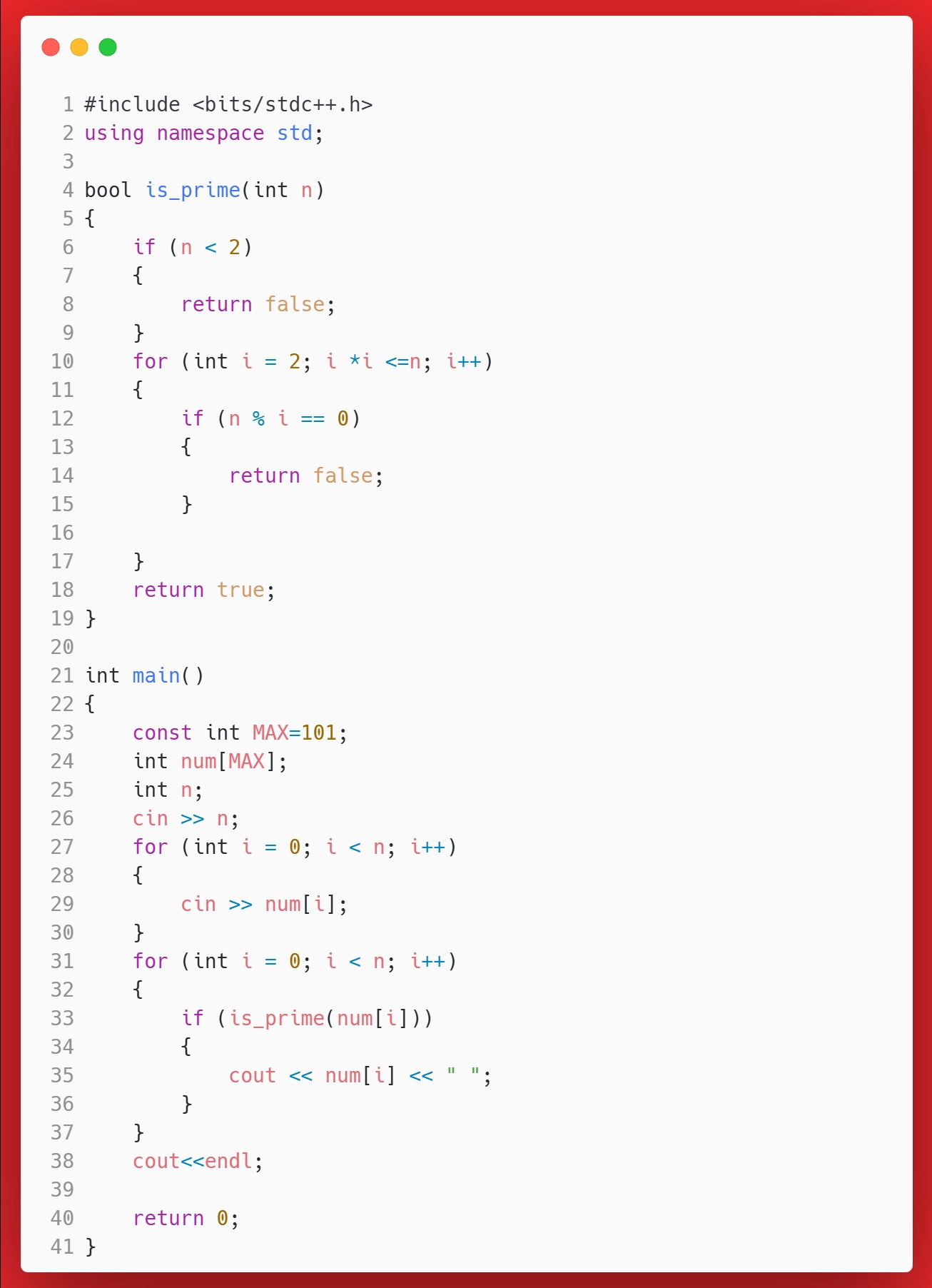
思考
本题展示了函数封装重复逻辑的好处。虽然叫“质数筛”,但实际是逐个判定,更高效的埃拉托斯特尼筛适合大范围筛质数。
