本页面已浏览879次

阿基米德（Archimedes）（公元前287年——公元前212年）——生平与成就

阿基米德最为人熟知的事，就是他发现如何判断一顶皇冠是纯金的还是掺了其它东西时，他从浴缸里跳了出来，光着身子在街上跑，大叫着“尤里卡！尤里卡！（Eureka！我发现了！）”。较少为人所知的是，他还发明了一种测试来将古代最伟大的数学家——也就是他自己——与那些沽名钓誉的骗子们加以区分。古希腊的数学世界中，很常见的一种情形是，数学家公布了他们最新发现的数学定理，但却不提供相应的证明。如果阿基米德怀疑他人冒领他的成果，他会在他的公布里插入两到三个命题——这些命题需要用到他所有的数学才华才能被证伪。一旦冒领者宣称这些伪命题是他们自己新发现的真理，他就发布一些反例而将他们曝光。

对阿基米德的生平我们所知甚少。罗马将领马塞勒斯写道，他的某个士兵在公元前212年的第二次布匿战争中杀死了阿基米德。一般认为，阿基米德直到其生命终点的75岁高龄还在研究几何学，这就是说他应该生于公元前287年。阿基米德的父亲叫菲迪阿斯，是一位天文学家，生活、工作于西西里岛上的希腊城市叙拉古。他们的家庭可能与叙拉古王室有关系，而阿基米德和国王希戎二世更是亲密。

虽说和欧几里德一样，我们对其生平知之甚少，但两者的相似之处也到此为止了。欧几里德是一位编纂者，他自己在数学上获得的成就寥寥可数——如果还谈得上有的话。但阿基米德是一位先驱，在数学和工程方面遥遥领先他的时代若干个世纪。事实上，阿基米德在古代最为人所知的是他为叙拉古王室所作出的工程上的成就。

希戎王曾挑战阿基米德，要他用很小的力量移动很重的物体。阿基米德设想了复合滑轮的概念，并表明他一个人就可以轻松地将一艘三桅船拉到岸边，而这本来需要100个男子费尽全力才可完成。按照古罗马传记作家普鲁塔克的说法，正是与这个传奇故事相关，阿基米德说出了他著名的一句话：“给我一个支点，我可以撬动地球”。

普鲁塔克和其他一些古代的学者（如波利比乌斯和李维）都提到了阿基米德为了保卫叙拉古，抵抗由马塞勒斯将军领导的罗马军队入侵而发明的一种了不起的弹射战争机器。普鲁塔克写道：

……阿基米德开始启动他的机器，并立即向地面部队发射种种投射的武器。巨大的石块呼啸着从天重重砸下，没有人能抵挡。它们成堆成堆地击倒它们所砸到的队伍，破坏了他们的队形。与此同时，巨大的杆子从墙上伸出来，搭在船上，凭着来自上方的大力将一些船弄沉；要么用一个铁钩或者类似吊车臂的钩子将一些船举起在空中，而一旦这些机器吊住了船首，将其头上尾下地挂起来后，机器将船埋向海底；还有一些别的船，被城内的机器拉住，打着转地撞向城墙上突出的峭壁，对船上的士兵造成了巨大的伤害。一艘船经常会被举到空中很高的地方——想想就是很可怕的事情——被来回翻动，不断的摆动，直到所有的水手都被甩了出来，最后船撞向岩石或者由空自由坠落。

阿基米德很容易完全投入到问题中而全然不顾其周遭发生了什么。普鲁塔克这样写道：

阿基米德的仆人们经常要逆着他的意愿而拖他去洗澡，为他涂抹香油。而即使在彼时彼地，他也会在烟囱的余烬上画出几何图形。而在为他涂油或者香料时，他的手指也在他的赤身裸体上画着线。他是如此地漫不经心，被几何研究所能带来的快乐带向恍惚忘形之境。

他这一忽视周遭的习性最终要了他的命。阿基米德工程方面的成就，制造出的战争机器，使他成为公元前287年第二次布匿战争期间入侵西西里的罗马军队的首要目标。传说是这样的：一位罗马士兵发现阿基米德正在沙盘上作图并命令他停下他的工作立即离开。阿基米德请求多一些时间来解决沙盘上的问题。这位士兵暴怒了，他破坏了阿基米德在沙盘上的图形，一剑刺穿了阿基米德！

阿基米德的数学成就主要有三个方面：

• 证明了由曲线和平面包围的立体的面积和体积的定理。收录于其著作《论球与圆柱》，《论圆的测量》，《方法论》 。
• 对静力学和静水力学问题的几何分析。
• 其它著作，特别是那些论及计数的文章，如《沙数记》。

本卷包括《沙数记》，《论球与圆柱》，《论圆的测量》和《方法论》四篇。

我们所知的《论圆的测量》的版本和阿基米德的其它著作有很大不同。它只有三个命题。而其中的第二个命题将圆的面积与以其直径为边长的正方形面积相比，又取决于第三个命题。这第三个命题说明圆的周长与直径的比值比3又1/7大，比3又10/71小。这是π的一个很精确的近似值。

我们最感兴趣的其第一个命题。它表明，一个圆的面积等于这样一个直角三角形的面积，其一个直角边等于半径之长，而另一直角边等于圆的周长。我们注意到阿基米德的这个结论——即将被曲线包围的面积（圆的面积）等同于被直线包围的面积（直角三角形的面积）——的表述是很有趣的。我们现代人将圆的面积表述为\(\pi r^2\)。阿基米德的表述用现代数学语言表示就是\(1/2(2\pi r)r\)。

在证明被曲线或者平面包围的形状的面积或者体积时，阿基米德使用了“穷举法”，也有时被称为“间接求极限”法。这一方法与阿基米德的引理齐名。该引理说：“给定两不等的线、面或立体，大者比小者多出的量，而该量自我相加得到的量可以超过与其本身及相互之间可比的任意指定的量。”阿基米德通常在归谬法证明中使用这些工具。

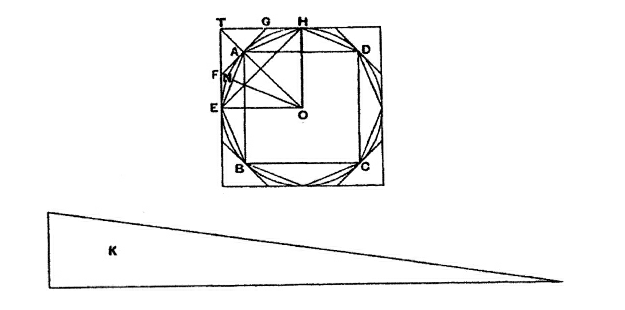
阿基米德这样开始证明。他意识到如果圆ABCD的面积不等于直角三角形K的面积（K的两条直角边分别是圆的半径和周长），那么圆的面积要么大于，要么小于K。证明的第一部分是假定圆的面积大于直角三角形K的面积。首先他在圆内做出一个内接正方形ABCD。接着他平分弧AB，BC，CD和DA，再将这些平分后的弧继续平分，直到由这些不断平分弧得到的顶点所构成的内接多边形和圆是如此接近，从而圆周和该内接多边形之间留下来的面积要比我们假定的圆和K之间的面积差还要小。因此，他得出结论，该内接多边形的面积要比K大。

接着，他考虑从圆O到AE边的垂线ON。既然AE是圆内切多边形的一条边，ON必定小于圆的半径，而多边形的周长也小于圆的周长（也就是直角三角形K的另一边）。因此，该内切多边形的面积必定小于直角三角形K的面积，和我们假定的矛盾。该证明的另一部分表明圆的面积也不会小于K的面积。

很多阿基米德证明的定理，在他之前的表述或者证明都是不充分的。但是他还是发现了好些重要的新规则。《方法论》简要描述了他是如何发现待证的新定理的。在其《论球与圆柱》一文的前言中，阿基米德这样写道：

自此，一些至今还没有证明的定理进入了我的视野，而我已经给出了它们的证明。这些定理有：一，任何球体的表面积是它最大半径圆的面积的四倍（现代表述法为\(4\pi r^2\)）……这些特性一直以来就是所谈到的图形自然固有的……但是却不为我之前那些研究几何的人所知。但现在既然已经发现这些属性对于这些图形是正确的，我会毫不犹豫地将其与我之前的研究并列，和欧多索克斯关于立体的那些定理并列，它们无可辩驳地成立，即任何圆锥的体积是其等底等高圆柱体的1/3。尽管这些性质一直以来如此自然地为这些图形所固有，事实上所有众多有能力的、生活在欧多克索斯之前的几何学者并不知晓，也没有被任何人观察到。如今，这些性质既已公开，即供拥有相应必备能力之诸君对鄙人之发现加以检验。

在所有已知的阿基米德著作中，《方法论》的历史最为有趣。多个世纪以来，只有10世纪的百科作家苏达斯语焉不详地提到这本书。而他也是引用比提尼亚的迪奥多西在阿基米德逝世后一个世纪所讲的一句话。数学家一直有着令其不安的奢望，希望找到寻求结果的宇宙通则。事实上笛卡尔就怀疑阿基米德压住《方法论》不发，从而任何人都不能从中得益。

1899年，希腊学者克拉缪斯报告说在土耳其的伊斯坦布尔的一座图书馆内发现了一份数学的重写本。所谓“重写本”是指一篇古代文档，其原来的内容被洗去使得可以在其上书写新的内容。读了几行克拉缪斯发布的手稿后，丹麦经典学者海贝尔认出了标志性的阿基米德风格。他怀疑隐藏在下面的手稿一定是阿基米德的作品。海贝尔在亲自检查该重写本的时候一定是惊讶万分。克拉缪斯找到了失传已久的作品《方法论》。其开篇写道：“阿基米德致埃拉托色尼以问候”。重写本里发现的其他阿基米德的作品更确认了作者的身份。

克拉缪斯——海贝尔重写本最早成于10世纪。在13世纪，一位僧侣洗去了原来的墨迹以便他可以为虔诚的祷告者写一本书。这位僧侣一定对他洗去了什么一无所知。他也无法想象该重写本未来的价值。1998年，克里斯蒂拍卖行以200万美元的高价拍出此书！

在《方法论》中，阿基米德所用的技术是假定固体是有密度一致的平面元素所构成。一个任意立体X的体积可以通过将其与另一个或另两个形状B和C一同放置在一根轴上来得到。阿基米德假定所有这些形状都被平行的平面切割，而这些平面都与该轴垂直。他这样来选择B和C使得：

• 它们的重心以及他们平面元素的重心都位于选定的轴上。
• 它们的体积已知。
• B的平面元素（可能需要和C一起）可以与X的平面元素相比。

最后的这个要求需要研究人员找到适合用来计算X的体积的图形B和C。一旦阿基米德确定了相应平面元素之间的关系，他会将轴延长到点τ，使得τφ的长度适合本题——这又是对研究人员创造性的要求——而这被当作是以φ为支点的杠杆。

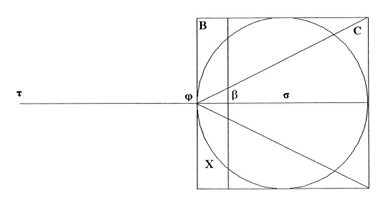
对于X的每个平面元素x（如果问题中需要C的，那么C的每个可能的c），他放置一个面积相等的元素y并使其重心在τ，因此y在τ的作用就平衡了对应的平面元素b在β点的作用，也就是说，y:b=φβ:φτ。接着，阿基米德考虑由平面元素y构成的Y。它的体积等于X的体积（也许要加上C），而Y是一个密度一致的立体，阿基米德的结论是它的重心在τ。由于所有在τ点的部分的作用平衡了所有B的部分在支点β的作用，那么所有Y成分在τ的作用平衡了所有B在其重心σ的作用。选择B时，其体积（也就是重量）和（在轴上的）重心是已知的。因此，阿基米德可以按照下列公式判定组合Y的体积：Y:B=φσ:φτ，因此他得到结论X=Y（或者X=Y-C）。

这本书的完整标题《处理力学问题之阿基米德之法》，强调说明了阿基米德的观点，即著作中包含的证明并不能称为数学证明。《方法论》中的证明依赖于用到图形的假设以及杠杆原理。这是力学原理！

只要给他一个正确的杠杆，阿基米德不仅能撬动地球，他还可以发现新的数学真理！